Blog
2019-01-01
It's 2019, and the Advent calendar has disappeared, so it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, Santa was able to work out who had stolen the presents and save Christmas:
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar, reveal the solution and a couple of notes and Easter eggs.
Highlights
My first highlight is the first puzzle in the calendar. This is one of my favourites as it has a pleasingly neat solution involving a
surprise appearance of a very famous sequence.
1 December
There are 5 ways to write 4 as the sum of 1s and 2s:
- 1+1+1+1
- 2+1+1
- 1+2+1
- 1+1+2
- 2+2
Today's number is the number of ways you can write 12 as the sum of 1s and 2s.
My next highlight is a puzzle that I was particularly proud of cooking up: again, this puzzle at first glance seems like it'll take a
lot of brute force to solve, but has a surprisingly neat solution.
10 December
The equation \(x^2+1512x+414720=0\) has two integer solutions.
Today's number is the number of (positive or negative) integers \(b\) such that \(x^2+bx+414720=0\) has two integer solutions.
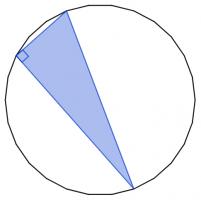
My next highlight is a geometry problem that appears to be about polygons, but actually it's about a secret circle.
12 December
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
My final highlight is a puzzle about the expansion of a fraction in different bases.
22 December
In base 2, 1/24 is
0.0000101010101010101010101010...
In base 3, 1/24 is
0.0010101010101010101010101010...
In base 4, 1/24 is
0.0022222222222222222222222222...
In base 5, 1/24 is
0.0101010101010101010101010101...
In base 6, 1/24 is
0.013.
Therefore base 6 is the lowest base in which 1/24 has a finite number of digits.
Today's number is the smallest base in which 1/10890 has a finite number of digits.
Note: 1/24 always represents 1 divided by twenty-four (ie the 24 is written in decimal).
Notes and Easter eggs
I had a lot of fun this year coming up with the names for the possible theives. In order to sensibly colour code each suspect's clues,
there is a name of a colour hidden within each name:
Fred Metcalfe,
Jo Ranger,
Bob Luey,
Meg Reeny, and
Kip Urples.
Fred Metcalfe's colour is contained entirely within his forename, so you may be wondering
where his surname came from. His surname is shared with Paul Metcalfe—the real name of a captain whose codename was a certain shade of red.
On 20 December, Elijah Kuhn emailed me to point out that it was possible to solve the final puzzle a few days early: although he could not yet work
out the full details of everyone's timetable, he had enough information to correctly work out who the culprit was and between which times the theft
had taken place.
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. This year, I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
13,
24, and
10 December;
and the easiest puzzles were on
5,
23,
11, and
15 December.
I also snuck a small Easter egg into the door arrangement: the doors were arranged to make a magic square, with each row and column, plus the two diagonals, adding to 55.
The solutions to all the individual puzzles can be found here. Using the clues, you can work out that everyone's seven activities
formed the following timetable.
| Bob Luey | Fred Metcalfe | Jo Ranger | Kip Urples | Meg Reeny |
| 0:00–1:21 Billiards | 0:00–2:52 Maths puzzles | 0:00–2:33 Maths puzzles | 0:00–1:21 Billiards | 0:00–1:10 Ice skating |
| 1:10–2:33 Skiing | ||||
| 1:21–2:52 Ice skating | 1:21–2:52 Stealing presents | |||
| 2:33–4:45 Billiards | 2:33–4:45 Billiards | |||
| 2:52–3:30 Lunch | 2:52–3:30 Lunch | 2:52–3:30 Lunch | ||
| 3:30–4:45 Climbing | 3:30–4:45 Climbing | 3:30–4:45 Climbing | ||
| 4:45–5:42 Curling | 4:45–5:42 Curling | 4:45–5:42 Curling | 4:45–5:42 Curling | 4:45–5:42 Lunch |
| 5:42–7:30 Maths puzzles | 5:42–7:30 Ice skating | 5:42–7:30 Chess | 5:42–7:30 Chess | 5:42–7:30 Maths puzzles |
| 7:30–10:00 Skiing | 7:30–9:45 Chess | 7:30–8:45 Skiing | 7:30–10:00 Maths puzzles | 7:30–9:45 Chess |
| 8:45–9:45 Lunch | ||||
| 9:45–10:00 Table tennis | 9:45–10:00 Table tennis | 9:45–10:00 Table tennis | ||
Following your investigation, Santa found all the presents hidden under Kip Urples's bed, fired Kip and sucessfully delivered all the presents
on Christmas Eve.
The winners
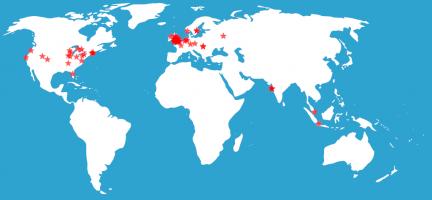
And finally (and maybe most importantly), on to the winners: 73 people submitted answers to the final logic puzzle. Their (very) approximate locations are shown on this map:
From the correct answers, the following 10 winners were selected:
| 1 | Sarah Brook |
| 2 | Mihai Zsisku |
| 3 | Bhavik Mehta |
| 4 | Peter Byrne |
| 5 | Martin Harris |
| 6 | Gert-Jan de Vries |
| 7 | Lyra |
| 8 | James O'Driscoll |
| 9 | Harry Poole |
| 10 | Albert Wood |
Congratulations! Your prizes will be on their way shortly. Additionally, well done to
Alan Buck, Alex Ayres, Alex Bolton, Alex Lam, Alexander Ignatenkov, Alexandra Seceleanu, Andrew Turner, Ashwin Agarwal,
Becky Russell, Ben Reiniger, Brennan Dolson,
Carl Westerlund, Cheng Wai Koo, Christopher Embrey, Corbin Groothuis,
Dan Whitman, David, David Ault, David Kendel, Dennis Oltmanns,
Elijah Kuhn, Eric, Eric Kolbusz, Evan Louis Robinson,
Felix Breton, Fred Verheul,
Gregory Loges,
Hannah,
Jean-Noël Monette, Jessica Marsh, Joe Gage, Jon Palin, Jonathan Winfield,
Kai Lam,
Louis de Mendonca,
M Oostrom, Martine Vijn Nome, Matt Hutton, Matthew S, Matthew Wales, Michael DeLyser, MikeKim,
Naomi Bowler,
Pranshu Gaba,
Rachel Bentley, Raymond Arndorfer, Rick Simineo, Roni, Rosie Paterson,
Sam Hartburn, Scott, Sheby, Shivanshi, Stephen Cappella, Steve Paget,
Thomas Smith, Tony Mann,
Valentin Vălciu, Yasha Ayyari, Zack Wolske, and Zoe Griffiths, who all also submitted the correct answer but were too unlucky to win prizes
this time.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-12-23
Recently, I made myself a new Christmas decoration:
Loyal readers may recognise the Platonic solid presents from last year's Christmas card, last year's
Advent calendar medals, or this year's Advent calendar medals.
If you'd like to make your own Platonic solids Christmas cross stitch, you can find the instructions below. I'm also currently putting together
some prototype Platonic solids cross stitch kits (that may be available to buy at some point in the future),
and will be adding these to the piles of prizes for this year's Advent calendar.
You will need
- A cross stitch needle
- Red cross stitch thread (for the ribbon)
- Black cross stitch thread (for the outlines)
- Non-red cross stitch thread (for the wrapping paper: I chose a different colour for each solid)
- Cross stitch aida
Instructions
Cross stitch thread is made up of 6 strands twisted together. When doing your cross stitch, it's best to use two strands at a time:
so start by cutting a sensible length of thread and splitting this into pairs of strands. Thread one pair of strands into the needle.
Following the patterns below, cross stitch rows of red and non-red crosses. To stitch a row, first go along the row sewing diagonals in one direction,
then go back along the row sewing the other diagonals. When you've finished the row, move the the row above and repeat. This is shown in the
animation below.
When doing the first row, make sure the stiches on the back cover the loose end of thread to hold it in place. Looking at the back of the
aida, it should look something like this:
When you are running out of thread, or you have finished a colour, finish a stitch so the needle is at the back.
Then pass the needle through some of the stitches on the back so that the loose end will be held in place.
The patterns for each solid are shown below. For each shape, the left pattern shows which colours you should cross in each square
(/ means red, o means non-red); and the right pattern shows where to add black lines after the crosses are all done.

Pattern for a tetrahedron (click to enlarge)

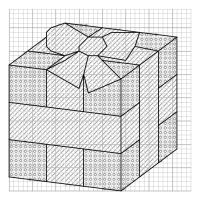
Pattern for a cube (click to enlarge)

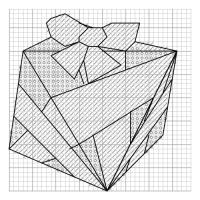
Pattern for a octahedron (click to enlarge)

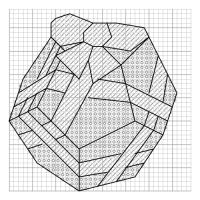
Pattern for a dodecahedron (click to enlarge)

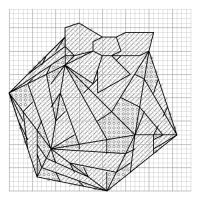
Pattern for a icosahedron (click to enlarge)
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-12-08
Just like last year and the year before, TD and I spent some time in November this year designing a Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 10 puzzles. By splitting the answers into pairs of digits, then drawing lines between the dots on the cover for each pair of digits (eg if an answer is 201304, draw a line from dot 20 to dot 13 and another line from dot 13 to dot 4), you will reveal a Christmas themed picture. Colouring the region of the card labelled R red or orange will make this picture even nicer.
If you want to try the card yourself, you can download this pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will be automatically be split into pairs of digits, lines will be drawn between the pairs, and the red region will be coloured...
If you enjoy these puzzles, then you'll almost certainly enjoy this year's puzzle Advent calendar.
| 1. | What is the smallest four digit number whose digits add up to 6? | Answer |
| 2. | What is the length of the hypotenuse of a right angled triangle whose two shorter sides have lengths 152,560 and 114,420? | Answer |
| 3. | What is the lowest common multiple of 1346 and 196? | Answer |
| 4. | What is the sum of all the odd numbers between 0 and 698? | Answer |
| 5. | How many numbers are there between 100 and 10,000 that contain no 0, 1, 2, or 3? | Answer |
| 6. | How many factors (including 1 and the number itself) does the number \(2^{13}\times3^{19}\times5^9\times7^{39}\) have? | Answer |
| 7. | In a book with pages numbered from 1 to 16,020,308, what do the two page numbers on the centre spread add up to? | Answer |
| 8. | You think of a number, then make a second number by removing one of its digits. The sum of these two numbers is 18,745,225. What was your first number? | Answer |
| 9. | What is the largest number that cannot be written as \(13a+119b\), where \(a\) and \(b\) are positive integers or 0? | Answer |
| 10. | You start at the point (0,0) and are allowed to move one unit up or one unit right. How many different paths can you take to get to the point (7,6)? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@Carmel: It's not meant to check your answers. It only shows up red if the number you enter cannot be split into valid pairs (eg the number has an odd number of digits or one of the pairs of digits is greater than 20).
Matthew
Great puzzle problems! Hint on #9: try starting with an analogous problem using smaller numbers (e.g. 3a + 10b). This helped me to see what I had to do more generally.
Noah
Add a Comment
2018-11-25
This year, the front page of mscroggs.co.uk will once again feature an advent calendar, just like last year, the year before and the year before. Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a logic puzzle:
It's nearly Christmas and something terrible has happened: one of Santa's five helpers—Fred Metcalfe, Jo Ranger, Meg Reeny, Bob Luey, and Kip Urples—has stolen all the presents during the North Pole's annual Sevenstival. You need to find the culprit before Christmas is ruined for everyone.
Every year in late November, Santa is called away from the North Pole for a ten hour meeting in which a judgemental group of elders decide who has been good and who has been naughty. While Santa is away, it is traditional for his helpers celebrate Sevenstival.
Sevenstival gets its name from the requirement that every helper must take part in exactly seven activities during the celebration; this year's
available activities were billiards, curling, having lunch, solving maths puzzles, table tennis, skiing, chess, climbing and ice skating.
Each activity must be completed in one solid block: it is forbidden to spend some time doing an activity, take a break to do something else then return to the first activity.
This year's Sevenstival took place between 0:00 and 10:00 (North Pole standard time).
During this year's Sevenstival, one of Santa's helpers spent the time for one of their seven activities stealing all the presents from Santa's workshop.
Santa's helpers have 24 pieces of information to give to you, but the culprit is going to lie about everything in an attempt to confuse you, so be careful who you trust.
Behind each day (except Christmas Day), there is a puzzle with a three-digit answer.
Each of these answers forms part of a fact that one of the helpers tells you.
You must work out who the culprit is and between which times the theft took place.
Ten randomly selected people who solve all the puzzles and submit their answers to the logic puzzle using the form behind the door on the 25th will win prizes!
The winners will also receive one of these medals:
As you solve the puzzles, your answers will be stored. To share your stored answers between multiple devices, enter your email address below the calendar and you will be emailed a magic link to visit on your other devices.
Behind the door on Christmas Day, there will be a form allowing you to submit your answers. The winner will be randomly chosen from all those who submit the correct answer before the end of 2018. Each day's puzzle (and the entry form on Christmas Day) will be available from 5:00am GMT. But as the winners will be selected randomly, there's no need to get up at 5am on Christmas Day to enter!
To win a prize, you must submit your entry before the end of 2018. Only one entry will be accepted per person. If you have any questions, ask them in the comments below or on Twitter.
So once December is here, get solving! Good luck and have a very merry Christmas!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-01-02
It's 2018, and the Advent calendar has disappeared, so it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, Santa was able to work out which present each child wanted, and get their presents to them just in time:
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar.
4 December
Pick a three digit number whose digits are all different.
Sort the digits into ascending and descending order to form two new numbers. Find the difference between these numbers.
Repeat this process until the number stops changing. The final result is today's number.
This puzzle revealed the surprising fact that repeatedly sorting the digits of a three digit number
into ascending and descending order then finding the difference will always give the same answer (as long as the digits of the starting number are all different).
This process is known as the Kaprekar mapping.
If four digit starting numbers are chosen, then all starting numbers that do not have three equal digits will eventually lead to 6174.
It's not as simple for five digit numbers, but I'll leave you to investigate this...
Ruben pointed something interesting out to me about this question: if you remove the constraint
that the answer must be a three digit number, then you see that the numbers 47, 497, 4997, 49997, and in fact any number of the form 49...97
will have this property.
20 December
What is the largest number that cannot be written in the form \(10a+27b\), where \(a\) and \(b\) are nonnegative integers (ie \(a\) and \(b\) can be 0, 1, 2, 3, ...)?
If you didn't manage to solve this one, I recommend trying replacing the 10 and 27 with smaller numbers (eg 3 and 4)
and solving the easier puzzle you get first, then trying to generalise the problem.
You can find my write up of this solution here.
Pedro Freitas (@pj_freitas) sent me a different way to approach this problem (related to solving the same question with different numbers on this year's Christmas card). To see his method, click "Show Answer & Extension" in the puzzle box above.
24 December
Today's number is the smallest number with exactly 28 factors (including 1 and the number itself as factors).
I really like the method I used to solve this one. To see it, click "Show Answer" above.
Solving all 24 puzzles lead to the following final logic puzzle:
Advent 2017 logic puzzle
2017's Advent calendar ended with a logic puzzle: It's nearly Christmas and something terrible has happened: Santa and his two elves have been cursed! The curse has led Santa to forget which present three children—Alex, Ben and Carol—want and where they live.
The elves can still remember everything about Alex, Ben and Carol, but the curse is causing them to lie. One of the elves will lie on even numbered days and tell the truth on odd numbered days; the other elf will lie on odd numbered days and tell the truth on even numbered days. As is common in elf culture, each elf wears the same coloured clothes every day.
Each child lives in a different place and wants a different present. (But a present may be equal to a home.) The homes and presents are each represented by a number from 1 to 9.
Here are the clues:
21
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
10
Orange hat says: "249 is my favourite number."
Orange hat says: "249 is my favourite number."
5
Red shoes says: "Alex lives at 1, 9 or 6."
Red shoes says: "Alex lives at 1, 9 or 6."
16
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
23
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
4
Blue shoes says: "495 is my favourite number."
Blue shoes says: "495 is my favourite number."
15
Blue shoes says: "Carol lives at 9, 6 or 8."
Blue shoes says: "Carol lives at 9, 6 or 8."
22
Purple trousers says: "Carol wants a factor of 294."
Purple trousers says: "Carol wants a factor of 294."
11
White shirt says: "497 is my favourite number."
White shirt says: "497 is my favourite number."
6
Pink shirt says: "Ben does not live at the last digit of 106."
Pink shirt says: "Ben does not live at the last digit of 106."
9
Blue shoes says: "Ben lives at 5, 1 or 2."
Blue shoes says: "Ben lives at 5, 1 or 2."
20
Orange hat says: "Carol wants the first digit of 233."
Orange hat says: "Carol wants the first digit of 233."
1
Red shoes says: "Alex wants 1, 2 or 3."
Red shoes says: "Alex wants 1, 2 or 3."
24
Green hat says: "The product of the six final presents and homes is 960."
Green hat says: "The product of the six final presents and homes is 960."
17
Grey trousers says: "Alex wants the first digit of 194."
Grey trousers says: "Alex wants the first digit of 194."
14
Pink shirt says: "One child lives at the first digit of 819."
Pink shirt says: "One child lives at the first digit of 819."
3
White shirt says: "Alex lives at 2, 1 or 6."
White shirt says: "Alex lives at 2, 1 or 6."
18
Green hat says: "Ben wants 1, 5 or 4."
Green hat says: "Ben wants 1, 5 or 4."
7
Green hat says: "Ben lives at 3, 4 or 3."
Green hat says: "Ben lives at 3, 4 or 3."
12
Grey trousers says: "Alex lives at 3, 1 or 5."
Grey trousers says: "Alex lives at 3, 1 or 5."
19
Purple trousers says: "Carol lives at 2, 6 or 8."
Purple trousers says: "Carol lives at 2, 6 or 8."
8
Red shoes says: "The digits of 529 are the toys the children want."
Red shoes says: "The digits of 529 are the toys the children want."
13
Green hat says: "One child lives at the first digit of 755."
Green hat says: "One child lives at the first digit of 755."
2
Red shoes says: "Alex wants 1, 4 or 2."
Red shoes says: "Alex wants 1, 4 or 2."
Together the clues reveal what each elf was wearing:

Drawn by Alison Clarke

Drawn by Adam Townsend
and allow you to work out where each child lives and what they wanted. Thanks Adam and Alison for drawing the elves for me.
I had a lot of fun finding place names with numbers in them to use as answers in the final puzzle. For the presents, I used the items from The 12 Days of Christmas:
| # | Location | Present |
| 1 | Maidstone, Kent | a partridge |
| 2 | Burcot, Worcestershire | turtle doves |
| 3 | Three Holes, Norfolk | French hens |
| 4 | Balfour, Orkney | calling birds |
| 5 | Fivehead, Somerset | gold rings |
| 6 | Sixpenny Handley, Dorset | geese |
| 7 | Sevenhampton, Glos | swans |
| 8 | Leighton Buzzard, Beds | maids |
| 9 | Nine Elms, Wiltshire | ladies |
I also snuck a small Easter egg into the calendar: the doors were arranged in a knight's tour, as shown below.
And finally (and maybe most importantly), on to the winners: 84 people submitted answers to the final logic puzzle. Their (very) approximate locations are shown on this map:
From the correct answers, the following 10 winners were selected:
| 1 | M Oostrom |
| 2 | Rosie Paterson |
| 3 | Jonathan Winfield |
| 4 | Lewis Dyer |
| 5 | Merrilyn |
| 6 | Sam Hartburn |
| 7 | Hannah Charman |
| 8 | David |
| 9 | Thomas Smith |
| 10 | Jessica Marsh |
Congratulations! Your prizes will be on their way shortly. Additionally, well done to Alan Buck, Alessandra Zhang, Alex Burlton, Alex Hartz, Alex Lam, Alexander, Alexander Bolton, Alexandra Seceleanu, Arturo, Brennan Dolson,
Carmen Günther, Connie, Dan Whitman, David Fox, David Kendel, Ed, Elijah Kuhn, Eva, Evan Louis Robinson, Felix Breton,
Fred Verheul, Henry Hung, Joakim Cronvall, Joe Gage, Jon Palin, Kai Lam, Keith Sutherland, Kelsey, Kenson Li, Koo Zhengqun,
Kristen Koenigs, Lance Nathan, Louis de Mendonca, Mark Stambaugh, Martin Harris, Martine Vijn Nome, Matt Hutton, Matthew Schulz, Max Nilsson, Michael DeLyser,
Michael Smith, Michael Ye, Mihai Zsisku, Mike Walters, Mikko, Naomi Bowler, Pattanun Wattana, Pietro Alessandro Murru, Raj, Rick,
Roni, Ross Milne, Ruben, Ryan Howerter, Samantha Duong, Sarah Brook, Shivanshi, Steve Paget, Steven Peplow, Steven Spence,
Tony Mann, Valentin Vălciu, Virgile Andreani, and Yasha Asley, who all also submitted the correct answer but were too unlucky to win prizes
this time.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Thanks! The advent calendar was great fun to take part in - and winning something in the process is the cherry on top. The riddles themselves were interesting and varied, they fitted well together in the overall puzzle, and I learned some interesting new bits of maths in the process. And now, to try my hand at the other advent calendars...
I particularly liked the riddle on the 5th of December (with walking 13 units) - it was quite tricky at first, but then I solved it by seeing that you can't end up on a square an even distance away from the centre, so the possible areas are in "circles" from the center with odd side lengths . It was quite reminiscent of showing you can't cover a chessboard with dominoes when two opposite corners are removed .
I particularly liked the riddle on the 5th of December (with walking 13 units) - it was quite tricky at first, but then I solved it by seeing that you can't end up on a square an even distance away from the centre, so the possible areas are in "circles" from the center with odd side lengths . It was quite reminiscent of showing you can't cover a chessboard with dominoes when two opposite corners are removed .
Lewis
Add a Comment