Blog
2017-03-27
Tomorrow, the new 12-sided one pound coin is released.
![](javascript:showlimage("one-pound.png"))
Although I'm excited about meeting this new coin, I am also a little sad,
as its release ends the era in which all British coins are shapes of constant
width.
Shapes of constant width
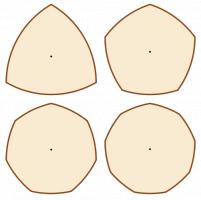
A shape of constant width is a shape that is the same width in every direction,
so these shapes can roll without changing height. The most obvious such shape
is a circle. But there are others, including the shape of the seven-sided 50p
coin.
![](javascript:showlimage("50p2008.jpg"))
As shown below, each side of a 50p is part of a circle centred around the opposite corner.
As a 50p rolls, its height is always the distance between one of the corners and
the side opposite, or in other words the radius of this circle. As these circles
are all the same size, the 50p is a shape of constant width.
![](javascript:showlimage("50p2008circle.jpg"))
Shapes of constant width can be created from any regular polygon with an
odd number of sides, by replacing the sides by parts of circles centred at the
opposite corner. The first few are shown below.
![](javascript:showlimage("Reuleaux_polygons.png"))
It's also possible to create shapes of constant width from irregular polygons with an odd number,
but it's not possible to create them from polygons with an even number of sides.
Therefore, the new 12-sided pound coin will be the first non-constant width British coin since
the (also 12-sided) threepenny bit was phased out in 1971.
Back in 2014, I wrote to my MP in an attempt to find
out why the new coin was not of a constant width. He forwarded my letter to
the Treasury, but I never heard back from them.
Pizza cutting
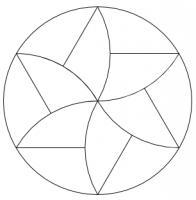
When cutting a pizza into equal shaped pieces, the usual approach is to
cut along a few diameters to make triangles. There are other ways to fairly
share pizza, including the following (that has appeared here before as an answer to this puzzle):
![](javascript:showlimage("pizza-answer.png"))
The slices in this solution are closely related to a triangle of constant
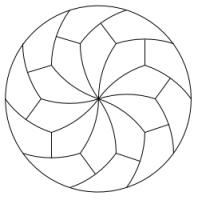
width. Solutions can be made using other shapes of constant width,
including the following, made using a constant width pentagon and heptagon (50p):
![](javascript:showlimage("pizza-answer-pent.png"))
![](javascript:showlimage("pizza-answer-hept.png"))
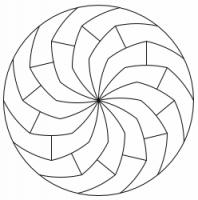
There are many more ways to cut a pizza into equal pieces. You can find them in Infinite families of monohedral disk tilings by Joel Haddley and Stephen Worsley [1].
You can't use the shape of a new pound coin to cut a pizza though.
Edit: Speaking of new £1 coins, I made this stupid video with Adam "Frownsend" Townsend about them earlier today:
References
[1] Infinite families of monohedral disk tilings by Joel Haddley and Stephen Worsley. December 2015. [link]
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment