Blog
2025-01-01
The puzzle on day 23 of this year's Advent calendar
is an interesting puzzle. After some hasty editing once it was pointed out to me that the original wording
was nonsense, the puzzle was this:
23 December
In a grid of squares, each square is friendly with itself and friendly with every square that is horizontally, vertically, or diagonally adjacent to it (and is not friendly with any other squares).
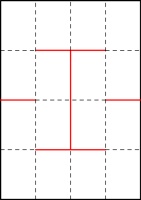
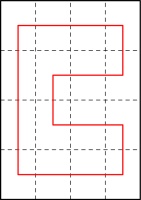
In a 5×5 grid, it is possible to colour 8 squares so that every square is friendly with at least two coloured squares:
![](javascript:showlimage("advent2024-23dec.png"))
It it not possible to do this by colouring fewer than 8 squares.
What is the fewest number of squares that need to be coloured in a
23×23 grid so that every square is friendly with at least two coloured squares?
As the squares that a square is friendly with are the same as those that would be attacked by a chess king on the square, the puzzle could be
re-expressed as: What is the fewest number of kings that need to be placed on a 23×23 chess board so that every square is attacked or occupied by at least two kings
(with no more than one king placed on each square)?
I came up with this puzzle while playing around with square grids in early November last year. I started by working out how many squares
need to be coloured for some smaller grids:
| Size of grid | Example grid | Minimum number of squares | ||||||||||||||||||||||||||||||||||||
| 2×2 | 2 | |||||||||||||||||||||||||||||||||||||
| 3×3 | 3 | |||||||||||||||||||||||||||||||||||||
| 4×4 | 8 | |||||||||||||||||||||||||||||||||||||
| 5×5 | 8 | |||||||||||||||||||||||||||||||||||||
| 6×6 | 10 |
This sequence was not on the OEIS, so I set about trying to work out the general formula for a term in this sequence.
Let \(a(n)\) be the minimum number of squared coloured for an \(n\) by \(n\) grid.
To work out the formula for \(a(n)\), we'll split the problem into 3 cases:
when \(n\) is a multiple of 3,
when \(n\) is 1 less than a multiple of 3,
when \(n\) is 2 less than a multiple of 3.
\(n=3k-1\)
When \(n\) is 1 less than a multiple of 3, it can be written as \(3k-1\) for some integer \(k\).
An upper bound
We can get an upper bound for the number of squares by finding a pattern of coloured squares that works, as the minimum number of squares will
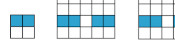
then be at most this. For a 2×2 grid, we can colour 2 squares like this:
For a 5×5 grid, we can colour 8 squares like this:
For an 8×8 grid, we can colour 18 squares like this:
We can continue this pattern: in general for a \((3k-1)\)×\((3k-1)\) grid, we colour in pairs of squares with a gap of one between them in every third row.
This would involve colouring \(k\) rows of \(2k\) squares, so a total of \(2k^2\) squares.
Therefore \(a(3k-1)\leqslant2k^2\).
A lower bound
To obtain a lower bound, consider these squares in 5×5 grid:
or these squares in 8×8 grid:
The squares that neighbour these highlighted squares do not overlap, so two different squares must be coloured for each of these. This means that at least
2×4 (for a 5×5 grid) and 2×9 (for a 8×8 grid) squares must be coloured.
Continuing the pattern of highlighting the squares in every third row and every third column, we see that for a \((2k-1)\)×\((2k-1)\) grid, we must colour
at least \(2k^2\) squares, and so \(a(3k-1)\geqslant2k^2\).
The general term
Combining the lower and upper bounds, we can see that \(2k^2\leqslant a(3k-1)\leqslant2k^2\), and so \(a(3k-1)=2k^2\). As 23 is one less than a multiple of 3,
this first case is enough to solve the puzzle in the Advent calendar.
\(n=3k-2\)
When \(n\) is 2 less than a multiple of 3, it can be written as \(3k-2\) for some integer \(k\). We can obtain upper and lower bounds in a very similar way.
An upper bound
To get an upper bound, consider this pattern of coloured squares:
For a \((3k-2)\)×\((3k-2)\) grid, this pattern involves colouring \(k\) rows of \(2k\) squares, and so \(a(3k-2)\leqslant2k^2\).
A lower bound
To get a lower bound, consider this pattern of highlighted squares:
In exactly the same was as for \(n=3k-1\), we can see from this pattern that \(a(3k-2)\geqslant2k^2\).
The general term
Once again, our upper and lower bounds are equal, and so \(a(3k-2)=2k^2\).
\(n=3k\)
Here's where this question gets trickier/more interesting. If \(n\) is a multiple of 3, then it can be written at \(3k\) for some integer \(k\).
An upper bound
We can obtain an upper bound from this pattern:
For a \(3k\)×\(3k\) grid, this pattern involved colouring \(k\) rows of \(2k+1\) squares, and so \(a(3k)\leqslant2k^2+k\).
A lower bound
As in the previous sections, we can get an lower bound using this pattern:
For a \(3k\)×\(3k\) grid, the lower bound requires at least \(2k^2\) squares to be coloured.
We can increase this lower bound by 1 by looking at the
bottom right corner: the previous lower bound can colour at most one square adjacent to this, so there must be at least one more square next to that corner coloured.
So we have arrived at the lower bound \(a(3k)\geqslant2k^2+1\).
Bounds
In this case, the lower and upper bounds are not the same, so we are left with \(2k^2+1\leqslant a(3k)\leqslant 2k^2+k\). I've written
a Python script to compute terms of this sequence and have used it to find that:
- \(a(3)=3\)
- \(a(6)=10\)
- \(a(9)=21\)
- \(a(12)=36\)
For \(n=12\) and larger than this, the script takes a very long time, so I haven't checked any more terms.
The sequence and a conjecture
Overall, we've shown that:
$$
a(n) = \begin{cases}
2k^2&\text{if }n=3k-1\\
2k^2&\text{if }n=3k-2\\
\text{between }2k^2+1\text{ and }2k^2+k&\text{if }n=3k
\end{cases}
$$
This can be written slightly more succinctly as (where \(\lfloor x\rfloor\) means \(x\) rounded down to an integer):
$$
a(n) = \begin{cases}
\text{between }2\left(\frac{n}3\right)^2+1\text{ and }2\left(\frac{n}3\right)^2+\frac{n}3&\text{if }n\text{ is a multiple of 3}\\
2\left\lfloor\frac{n+2}3\right\rfloor^2&\text{if }n\text{ is not a multiple of 3}
\end{cases}
$$
I've submitted the sequence I have so far to the OEIS: A379726.
Based on the terms computed above, I conjecture that \(a(3k)=2k^2 + k\). If you have any ideas how I could increase my lower bound, or for any other way I could prove this, let me know!
Edit: OEIS sequence is published!
×2 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Here is my solution:
Project
Pre-built
Probably not super useful as I didn't attempt to prove my results, but I did come up with a general formula for odd-sized squares (with floor and ceiling functions), and perhaps the way I decoupled the two dimensions could be a useful approach for you.
Project
Pre-built
Probably not super useful as I didn't attempt to prove my results, but I did come up with a general formula for odd-sized squares (with floor and ceiling functions), and perhaps the way I decoupled the two dimensions could be a useful approach for you.
Dan Whitman
The conjecture is correct. Super-brief sketch proof: divide the grid into 3x3 boxes, aggregate those into horizontal and vertical strips of width 1 box = 3 squares; say a strip is "cheap" if it contains only 2k shaded squares (hence, exactly two per box). Working box by box from one end of a cheap strip to the other in both directions we see that the shaded squares must be in the middle transverse row/column of each box in such a strip. Hence there can't be both a cheap horizontal strip and a cheap vertical strip, because the box where they meet is overconstrained. So either all h-strips are not-cheap or all v-strips are not-cheap, and either of those gives you at least 2k2+k shaded squares.
(This, along with everything M.S. wrote, generalizes straightforwardly to arbitrary rectangular grids.)×1 ×3
(This, along with everything M.S. wrote, generalizes straightforwardly to arbitrary rectangular grids.)
g
×1 ×3 Add a Comment
2024-02-20
Back in November, I wrote about making 2n-page zines.
Thanks to some conversations I had at Big MathsJam
in later November, I've been able to work out how many 128-page zines there are: 315434.
The insight
At Big MathsJam, Colin Beveridge pointed out
something he'd noticed about the possible zines: when drawing the line connecting the pages
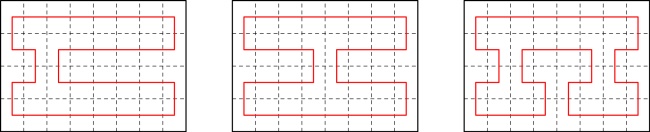
in order, there were some line segments that were always included. For example, here are all of the possible
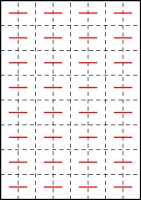
64-page zines:
![](javascript:showlimage("64zines.png"))
Every single one of these includes these line segments:
![](javascript:showlimage("64zines-always.png"))
Colin conjectured that for a zine of any size, a pattern like this of alternative horizontal segments
must always be included. He was close to justifying this, and since MathsJam I've been able to fill
in the full justificication.
The justificiation
First, consider the left-most column of pages. They must be connected like this:
![](javascript:showlimage("64zines-leftcol.png"))
If they were connected in any other way, there would be two vertical connections in a row,
which would create a page that is impossible to open (as every other connection must be a horizontal
that ends up in the spine). Additionally, the horizontal lines in this diagram must all be in the
spine (as otherwise we again get pages that cannot be opened).
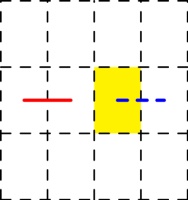
Next, consider a horizontal line that's in the spine (shown in red below), and we can look
at all the possible ways to draw the line through the highlighted page, paying particular
attention to the dashed blue line:
![](javascript:showlimage("64zines-highlighted.png"))
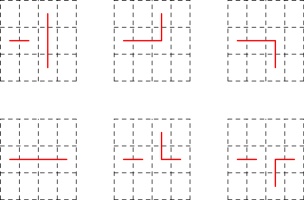
The six possible ways in which the line could travel through the highlighted page are:
![](javascript:showlimage("64zines-options.png"))
The three options in the top row do not give a valid zine: the leftmost diagram has two vertical
connections in a row (leading to pages that do not open). The other two diagrams in the top row
have the horizontal line that we know is in the spine, followed by a horizontal line not in the
spine, then a vertial line: this vertical line should be in the spine, but as it is vertical
it cannot be (without making a page that doesn't open).
In each of the diagrams in the bottom row, the connection shown in dashed blue
is included and must be in the spine: in the leftmost diagram, the horizontal line that we know is in the spine
is followed by a horizontal not in the spine, then the horizinal in the dashed blue position
that must therefore be in the spine. The othe other two diagrams in the bottom row,
the dashed blue position is connected to a vertical line: this means that the dashed blue connection
must be in the spine (as otherwise the vertical would cause a page that doesn't open).
Overall, we've now shown that the leftmost column of lines must always be included and
must all be in the spine; and for each horizontal line in the spine, the line to the right of it
after a single gap must also be included and in the spine. From this, it follows that all the horizontal
lines in Colin's pattern must always be included.
Calculating the number of 128-page zines
Now that I knew that all these horizonal lines are always included, I was able to update
the code I was using to find all the possible zines
to use this. After a few hours, it had found all 315434 possibilites. I was very happy to get this
total, as it was the same as the number that
Luna (another attendee of Big MathsJam) had calculated but wasn't certain was correct.
The sequence of the number of 2n-page zines,
including the newly calculated number,
is now published on the OEIS.
I think calculating number of 256-page zines is still beyond my code though...
×8 ×5 ×5 ×8(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2023-11-03
I showed off an unfinished version of the content in this blog post in the first
Finite Group live stream in October. I'll be showing off other upcoming things and other
content at future Finite Group events. If you'd like to watch this, you can sign up to our Patreon at
finitegroup.co.uk.
A few months ago at Cheltenham Science Festival, Hana Ayoob showed me how to make an 8-page zine.
If you've not make one before, I recommend following these steps now.
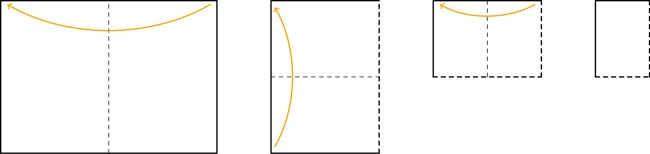
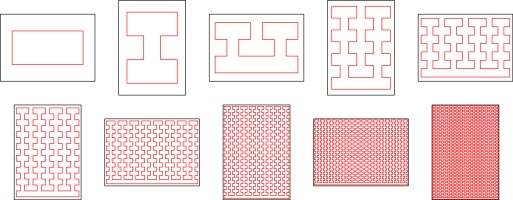
Take a piece of A4 paper, and fold it 3 times like this:
![](javascript:showlimage("8zine1.png"))
Unfold all the folds except the first one and cut along the red line:
![](javascript:showlimage("8zine2.png"))
After unfolding, your paper should look like this:
![](javascript:showlimage("8zine3.png"))
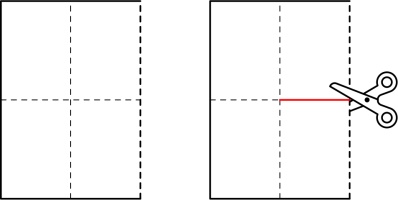
Fold the paper in half the other way:
![](javascript:showlimage("8zine4.png"))
Push the two ends of the paper together so that the front of the middle bit of paper comes forward,
and the back goes backward:
![](javascript:showlimage("8zine5.png"))
Finally, flatten all the pages and you have your zine:
![](javascript:showlimage("8zine6.png"))
You're now free to write or draw whatever you like on the 8 pages of your zine.
If you'd like to fold a zine that already has content printed on it, you can
print the instructions for the TMiP puzzle hunt that I wrote earlier this year, or you can print this blog post off in zine format.
A 16-page zine
If you're anything like me, you'll already be wondering if it's possible to do some more folding
and cutting to make a 16-page zine from a piece of A4. After some trial and error, I found that
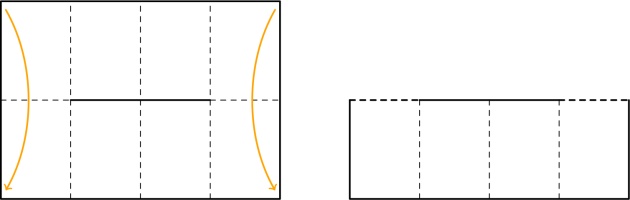
you can if you fold the paper 4 times then cut along these red lines:
![](javascript:showlimage("16zine1.png"))
(This time, I've drawn the diagram with a portrait piece of paper, as this leads to a portrait zine. For an 8-page zine, a landscape piece of paper led to a portrait zine.)
Instead of drawing which lines we need to cut, we can represent our two zines so far by drawing
lines that connect the pages in order:
![](javascript:showlimage("8and16zines.png"))
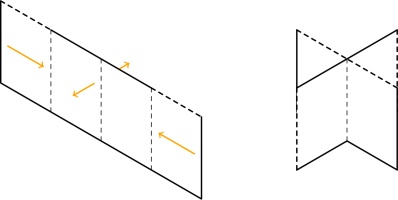
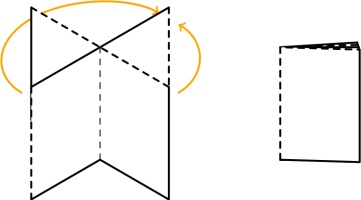
During my experimentation, I saw that every second connection between pages must be horizontal.
These horizontal connections end up in the spine of the zine and allow the pages to turn.
If you can't visualise why the pages won't turn if this condition doesn't hold, try making a 16-page
zine like this:
![](javascript:showlimage("failed16zine.png"))
32-page zines
Now that we can make a 16-page zine, the obvious question is: can we make a 32-page zine?
To answer this, we need to look for lines that go through all
32 pages where every second connection is a horizontal. I wrote a Python script to look for these and it
found 3:
![](javascript:showlimage("32zines.png"))
The code also told me that the 8- and 16-page zines we know about are the only 8- and 16-page
zines. I'm only counting the zines where the pages in the final zine are portrait, and have the same side ratio a the original piece of A4 paper:
there will be other possible zines where the pages are landscape that we aren't counting.
2n-page zines
Now that we have 8-page, 16-page, and 32-page zines, we can look for patterns that we
can generalise to make a 2n-page zine. This generalisation was the first I
came up with:
![](javascript:showlimage("2nzines.png"))
One possible 2n-page zine for n=3 to 12 (click to enlarge)
There are, of course, many other generalisations that you could come up with.
How many zines?
While working towards our generalised zine, you may have started pondering another question:
for any given n, how many different 2n-page zines can be made?
For n=2, there's only one way to make a zine (fold the paper twice).
For n=3 to 6, we've already seen that there are 1, 1, and 3 ways to make zines. The code
I wrote was also able to tell me that there are 31 possible 64-page zines:
All 31 possible 64-page zines (click to enlarge)
So the start of the sequence of the number of possible zines is: 1, 1, 1, 3, 31.
The number of different possible paths to check increases very quickly as we increase
n, so I was unable to compute the next term in a reasonable amount of time.
I've submitted this sequence to the OEIS. Let's
hope someone is able to work out the next term. If you're that someone, let me know!
×3 ×2 ×3 ×3 ×4(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2019-06-19
A308092 The sum of the first \(n\) terms of the sequence is the concatenation of the first \(n\) bits of the sequence read as binary, with \(a(1) = 1\).1, 2, 3, 7, 14, 28, 56, 112, 224, 448, 896, 1791, 3583, 7166, ...
To understand this definition, let's look at the first few terms of this sequence written in binary:
By "the concatenation of the first \(n\) bits of the sequence", it means the first \(n\) binary digits of the whole sequence written in order:
1, then 11, then 110, then 1101, then 11011, then 110111, and so on. So the definition means:
- The first term is 1, as given in the definition (\(a(1)=1\)).
- The sum of the first 2 terms is the first 2 digits: \(1+10=11\).
- The sum of the first 3 terms is the first 3 digits: \(1+10+11=110\).
- The sum of the first 4 terms is the first 4 digits: \(1+10+11+111=1101\).
- The sum of the first 5 terms is the first 5 digits: \(1+10+11+111+1110=11011\).
As we know that the sum of the first \(n-1\) terms is the first \(n-1\) digits, we can calculate the third term of this sequence onwards using:
"\(a(n)\) is the concatenation of the first \(n\) bits of the sequence subtract concatenation of the first \(n-1\) bits of the sequence":
- The third term is \(110 - 11 = 11\).
- The fourth term is \(1101 - 110 = 111\).
- The fourth term is \(11011 - 1101 = 1110\).
- The fifth term is \(110111 - 11011 = 11100\).
The conjecture
Peter's conjecture is that the number of 1s in each term is greater than or equal to the number of 1s in the previous term.
I'm going to prove this conjecture. If you'd like to have a try first, stop reading now and come back when you're ready for spoilers.
(If you'd like a hint, read the next section then pause again.)
Adding a digit
The third term of the sequence onwards can be calculated by subtracting the first \(n-1\) digits from the first \(n\) digits.
If the first \(n-1\) digits form a binary number \(x\), then the first \(n\) digits will be \(2x+d\), where \(d\) is the \(n\)th digit
(because moving all the digits to the left one place in binary is multiplying by two).
Therefore the different is \(2x+d-x=x+d\), and so we can work out the \(n\)th term of the sequence by adding the \(n\)th digit in the
sequence to the first \(n-1\) digits. (Hat tip to Martin Harris, who spotted this first.)
Carrying
Adding 1 to a binary number the ends in 1 will cause 1 to carry over to the left. This carrying will continue until the 1 is carried into
a position containing 0, and after this all the digits to the left of this 0 will remain unchanged.
Therefore adding a digit to
the first \(n-1\) digits can only change the digits from the rightmost 0 onwards.
Endings
We can therefore disregard all the digits before the rightmost 0, and look at how the \(n\)th term compares to the \((n-1)\)th term.
There are 5 ways in which the first \(n\) digits could end:
- \(00\)
- \(010\)
- \(01...10\) (where \(1...1\) is a string of 2 or more ones)
- \(01\)
- \(01...1\) (where \(1...1\) is again a string of 2 or more ones)
We now look at each of these in turn and show that the \(n\)th term will contain at least as many ones at the \((n-1)\)th term.
Case 1: \(00\)
If the first \(n\) digits of the sequence are \(x00\) (a binary number \(x\) followed by two zeros), then the \((n-1)\)th term of the
sequence is \(x+0=x\), and the \(n\)th term of the sequence is \(x0+0=x0\). Both \(x\) and \(x0\) contain the same number of ones.
Case 2: \(010\)
If the first \(n\) digits of the sequence are \(x010\), then the \((n-1)\)th term of the sequence is \(x0+1=x1\),
and the \(n\)th term of the sequence is \(x01+0=x01\). Both \(x1\) and \(x01\) contain the same number of ones.
Case 3: \(01...10\)
If the first \(n\) digits of the sequence are \(x01...10\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...10+1=x01...1\). \(x01...1\) contains more ones than \(x10...0\).
Case 4: \(01\)
If the first \(n\) digits of the sequence are \(x01\), then the \((n-1)\)th term of the sequence is \(x+0=x\),
and the \(n\)th term of the sequence is \(x0+1=x1\). \(x1\) contains one more one than \(x\).
Case 5: \(01...1\)
If the first \(n\) digits of the sequence are \(x01...1\), then the \((n-1)\)th term of the sequence is \(x01...1+1=x10...0\),
and the \(n\)th term of the sequence is \(x01...1+1=x10...0\). Both these contain the same number of ones.
In all five cases, the \(n\)th term contains more ones or an equal number of ones to the \((n-1)\)th term, and so the conjecture is true.
×1 ×1 ×1 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-10-08
During my Electromagnetic Field talk this year, I spoke about @mathslogicbot (now reloated to @logicbot@mathstodon.xyz and @logicbot.bsky.social), my Twitter bot that is working its way through the tautologies in propositional calculus. My talk included my conjecture that the number of tautologies of length \(n\) is an increasing sequence (except when \(n=8\)). After my talk, Henry Segerman suggested that I also look at the number of contradictions of length \(n\) to look for insights.
A contradiction is the opposite of a tautology: it is a formula that is False for every assignment of truth values to the variables. For example, here are a few contradictions:
$$\neg(a\leftrightarrow a)$$
$$\neg(a\rightarrow a)$$
$$(\neg a\wedge a)$$
$$(\neg a\leftrightarrow a)$$
The first eleven terms of the sequence whose \(n\)th term is the number of contradictions of length \(n\) are:
$$0, 0, 0, 0, 0, 6, 2, 20, 6, 127, 154$$
This sequence is A277275 on OEIS. A list of contractions can be found here.
For the same reasons as the sequence of tautologies, I would expect this sequence to be increasing. Surprisingly, it is not increasing for small values of \(n\), but I again conjecture that it is increasing after a certain point.
Properties of the sequences
There are some properties of the two sequences that we can show. Let \(a(n)\) be the number of tautolgies of length \(n\) and let \(b(n)\) be the number of contradictions of length \(n\).
First, the number of tautologies and contradictions, \(a(n)+b(n)\), (A277276) is an increasing sequence. This is due to the facts that \(a(n+1)\geq b(n)\) and \(b(n+1)\geq a(n)\), as every tautology of length \(n\) becomes a contraction of length \(n+1\) by appending a \(\neg\) to be start and vice versa.
This implies that for each \(n\), at most one of \(a\) and \(b\) can be decreasing at \(n\), as if both were decreasing, then \(a+b\) would be decreasing. Sadly, this doesn't seem to give us a way to prove the conjectures, but it is a small amount of progress towards them.
Edit: Added Mastodon and Bluesky links
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
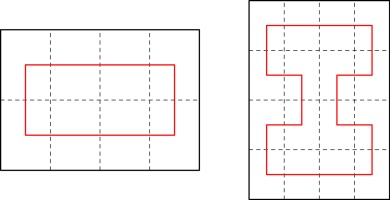
2x2: 6
3x3: 2
4x4: 1296
5x5: 371
6x6: 8
Haven't been able to go any farther with my current script, but for what it's worth, here it is on GitHub.