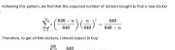Blog
2016-05-04
Back in 2014, I calculated the expected cost of
filling Panini world cup sticker album. I found that you should expect to buy
4505 stickers, or 1285 if you order the last 100 from the Panini website (this
includes the last 100). This would cost £413.24 or £133.99
respectively.
Euro 16 is getting close, so it's sticker time again. For the Euro 16
album there are 680 stickers to collect, 40 more than 2014's 640 stickers.
Using the same calculation method as before,
to fill the Euro 16 album, you should expect to buy 4828
stickers (£442.72), or 1400 (£134.32) if you order the last 100.
This, however, does not tell the whole story. Anyone who has collected
stickers as a child or an adult will know that half the fun comes from
swapping your doubles with friends. Getting stickers this way is not
taken into account in the above numbers.
Simulating a sticker collection
Including swaps makes the situation more complicated: too complicated
to easily calculate the expected cost of a full album. Instead, a different
method is needed. The cost of filling an album can be estimated by
simulating the collection lots of times and taking the average of the cost of
filling the album in each simulation. With enough simulations, this estimate
will be very close the the expected cost.
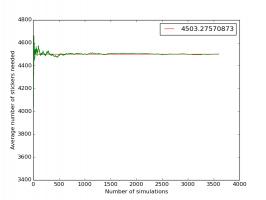
To get an accurate estimation, simulations are run,
calculating the running average as they go, until the running averages after recent simulations
are close together. (In the examples, I look for the four most recent running averages to be within 0.01.)
The plot below shows how the running average changes as more simulations are performed.
![](javascript:showlimage("1_ordering_0.png"))
The simulations estimate the number of stickers needed as 4500. This is
very close to the 4505 I calculated last year.
Now that the simulations are set up, they can be used to see what happens if you have friends to swap with.
What should I do?
The plots below shows how the number of stickers you need to buy each changes based on how many friends you have.
![](javascript:showlimage("ppl_ordering_0.png"))
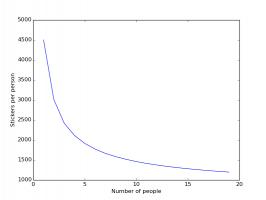
Stickers needed if you and your friends order no stickers.
![](javascript:showlimage("ppl_ordering_100.png"))
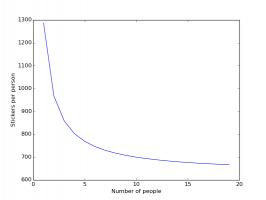
Stickers needed if you and your friends all order the last 100 stickers. The last 100 are not counted.
In both these cases, having friends reduces the number of stickers you need to buy significantly, with your first few friends
making the most difference.
Ordering the last 100 stickers looks to be a better idea than ordering no stickers. But how many stickers should you order to
minimise the cost? When you order stickers, you are guaranteed to get those that you need, but they cost more: ordered stickers cost 14p
each, while stickers in 6 pack multipacks come out at just 9.2p each. The next plot shows how the cost changes based on how many you order.
![](javascript:showlimage("sticker_money_8.png"))
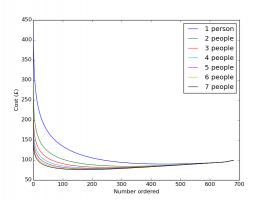
The expected cost of filling an album based on number of people in group and number of stickers ordered.
Each of the coloured curves represents a group of a different size. For each group, ordering no stickers works out the most
expensive—this is expected as so many stickers must be bought to find the last few stickers—and ordering all the stickers also works
out as not the best option. The best number to order
is somewhere in the middle, where the curve reaches its lowest point. The minimum points on each of these curves are summarised in the
next plots:
![](javascript:showlimage("ppl_vs_order_26.png"))
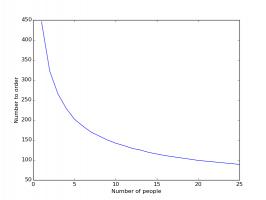
How the number you should order changes with the number of people in the group.
![](javascript:showlimage("ppl_vs_cost_26.png"))
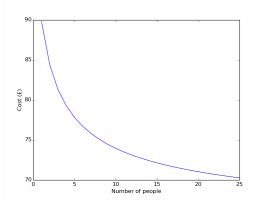
How the cost changes with the number of people in the group.
Again, having friends to swap with dramatically reduces the cost of filling an album. In fact, it will almost definitely pay off in future
swaps if you go out right now and buy starter packs for all your friends...
×1 ×1 ×1 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment