Blog
Tube map stellated rhombicuboctahedron
2015-03-24
This is the fourth post in a series of posts about tube map folding.
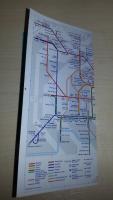
A while ago, I made this (a stellated rhombicuboctahedron):
![](javascript:showlimage("rhombi.jpg"))
Here are some hastily typed instructions for
Matt Parker, who is making one
at this month's Maths Jam. Other people are
welcome to follow these instructions too.
You will need
- 48 tube maps
- glue
Making a module
First, take a tube map and fold the cover over. This will ensure that your
shape will have tube (map and not index) on the outside and you will have
pages to tuck your tabs between later.
![](javascript:showlimage("rh_mp1.jpg"))
Now fold one corner diagonally across to another corner. It does not matter
which diagonal you chose for the first piece but after this all following pieces
must be the same as the first.
![](javascript:showlimage("rh_mp2.jpg"))
Now fold the overlapping bit back over the top.
![](javascript:showlimage("rh_mp3.jpg"))
Turn it over and fold this overlap over too.
![](javascript:showlimage("rh_mp4.jpg"))
You have made one module.
![](javascript:showlimage("rh_mp5.jpg"))
You will need 48 of these and some glue.
Putting it together
By slotting three or four of these modules together, you can make a
pyramid with a triangle or square as its base.
![](javascript:showlimage("rh_mp6.jpg"))
![](javascript:showlimage("rh_mp7.jpg"))
A stellated rhombicuboctahedron is a rhombicuboctahedron with a pyramid, or
stellation on each face. In other words, you now need to build a
rhombicuboctahedron with the bases of pyramids like these. A rhombicuboctahedron
looks like this:
![](javascript:showlimage("rh_mp_wik.jpg"))
en.wiki User Cyp, CC BY-SA 3.0
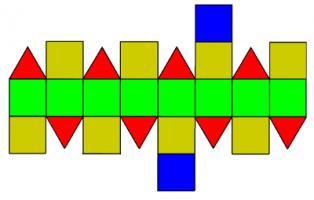
More usefully, its net looks like this:
![](javascript:showlimage("rh_mp_net.png"))
To build a stellated rhombicuboctahedron, make this net, but with each shape
as the base of a pyramid. This is what it will look like 6/48 tube maps in:
![](javascript:showlimage("rh_mp8.jpg"))
If you make on of these, please tweet me a photo so I can see it!
![](javascript:showlimage("rh_mp_fin.jpg"))
Previous post in series
This is the fourth post in a series of posts about tube map folding.
Next post in series
×2 ×2 ×2 ×2 ×2(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2017-10-14) ⭐
I wish you'd make the final stellation of the rhombicuboctahedron! And show us! I know the shapes of the faces but have been stuck two years on the assembly!Roberts, David
×2 ×2 ×2 ×2 ×2 Add a Comment