Advent calendar 2018
12 December
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
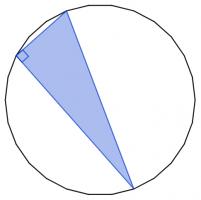
These three vertices form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
Show answer
Hide answer
The vertices of the 26-gon lie on a circle. The triangle is therefore right-angled if (and only if) the longest side is a diameter of the circle.
In other words, the triangle is right angled if (and only if) two of its vertices are opposite vertices of the 26-gon.
There are 13 different pairs of opposite points on the 26-gon. For each of these, there are 24 remaining vertices that could be the third vertex of the triangle.
Therefore there are 13×24=312 different right angled triangles.
![](javascript:showlimage("advent2018-12.png"))