Blog
Solving the cross diagonal cover problem
2016-07-04
In five blog posts
(1,
2,
3,
4,
5)
Gaurish Korpal present the Cross diagonal cover problem, some ideas about how to solve it and some conjectures.
In this post, I will present my solution to this problem. But first, the problem itself:
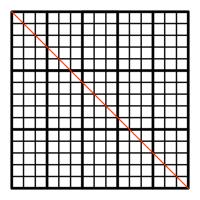
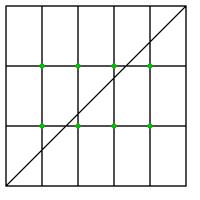
Draw with an \(m\times n\) rectangle, split into unit squares. Starting in the top left corner, move at 45° across
the rectangle. When you reach the side, bounce off. Continue until you reach another corner of the rectangle:
![](javascript:showlimage("cross_p1.png"))
![](javascript:showlimage("cross_p2.png"))
![](javascript:showlimage("cross_p3.png"))
![](javascript:showlimage("cross_p4.png"))
![](javascript:showlimage("cross_p5.png"))
![](javascript:showlimage("cross_pend.png"))
How many squares will be coloured in when the process ends?
Restating the problem
When I first saw this problem, it reminded me of Rebounds, a puzzle I posted here
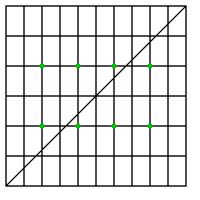
in 2014. To restate the problem in a similar way, we place a point in the centre of each unit square,
then creating a second grid. I will call this the dual grid. The original problem is equivalent to asking, if a line bounces
around the dual grid, how many corners will it pass through.
![](javascript:showlimage("cross_2.png"))
![](javascript:showlimage("cross_2_2.png"))
It it worth noting here that the dual grid is \(n-1\times m-1\): each side is one shorter than the original grid.
A corner cannot be travelled over more than twice: otherwise, the line would be retracing its past path; to do this requires it to have
already hit a corner of the rectangle. Therefore we can calculate the number of distinct corners travelled to using:
$$\text{Distinct corners visited} = \text{Corners visited}-\text{Corners visited twice}$$
Introducing mirrors
When I solved Rebounds, I imagined the line passing through mirror images of the rectange, rather then bouncing.
For our example above, it would look like this:
![](javascript:showlimage("cross_3.png"))
Looking at the puzzle in this way, it can be seen that the line will travel through \(\mathrm{lcm}(n-1,m-1)\) squares, and so hit \(\mathrm{lcm}(n-1,m-1)+1\)
corners (the \(+1\) appears due to fence panels and fence posts).
We have shown that:
$$\text{Corners visited}=\mathrm{lcm}(n-1,m-1)+1$$
Collisions in the mirror
To solve the problem, we need to work out how many corners are visited twice; or the number of times the line crosses itself in the rectangle.
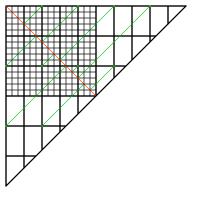
To do this, imagine the mirror images of the red line in the mirrors. Ignoring the images parallel to the red line, and terminating
the lines when they hit the red line gives the following diagram:
![](javascript:showlimage("cross_4.png"))
I have added extra rectangles to the diagram so that all the reflections that hit the red line and their starting points can be seen.
The diagonal black line has been added because all lines outside that clearly cannot intersect the red line.
We now need to justify two claims:
- Each intersection of a red line and a green line corresponds to the line bouncing off the side of the rectangle or crossing itself (in the dual rectangle). Each bounce or crossing matches with exactly one red-green intersection.
- The green lines starting on the outer border are those that correspond to the bounces.
The first claim can be seen by reflecting the green lines and the parts of the red line they hit back into the top left rectangle.
The second claim can be shown in two parts:
First, each line starting from the border will meet the red line on the edge of a rectangle:
this is because the green lines all start a multiple of two rectangles away, and meet at half this distance away (and half a multiple of two
is a whole number).
Conversely, if a red line meets a green line at the edge of a rectangle, then the reflection of the red line in the edge (ie. the green line)
must go back to a starting point on the boundary.
These two claims show that the points where the line crosses itself in the dual rectangle match up one-to-one with the interior points
at which the green lines start. So if we can count these points, we can solve the problem.
Counting the interior points
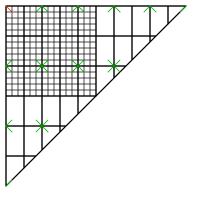
The green lines will start from all points that are a multiple of two rectangles (in both directions) away from the top left. The reason for
this can be seen by reflecting the first little bit of the red line in all the mirrors:
![](javascript:showlimage("cross_why.png"))
We see that the perpendicular green lines that we are interested in, plus many other irrelevant lines, start from a grid of points on the
corner of every other rectangle. To count these points, we will extend them into the full square:
![](javascript:showlimage("cross_5.png"))
To make for clearer counting, I have not drawn the unit squares.
Alternatively, this square can be thought of as being made up from two copies of the triangle.
We next notice that these points can never lie on the diagonal (the diagonal drawn in the diagram): a green point lying on the diagonal would imply
that the red line met a corner before it did. Taking out the lines on which the green dots never lie, we get:
![](javascript:showlimage("cross_6.png"))
We can now count the green dots. In the square above, there are
\(\displaystyle\frac{\mathrm{lcm}(m-1,n-1)}{m-1}\) rectangles vertically and
\(\displaystyle\frac{\mathrm{lcm}(m-1,n-1)}{n-1}\) rectangles horizontally.
Therefore there are
\(\displaystyle\frac{\mathrm{lcm}(m-1,n-1)}{m-1}-1\) columns of green dots and
\(\displaystyle\frac{\mathrm{lcm}(m-1,n-1)}{n-1}-1\) rows of green dots. (Again, we take one due to fence posts and fence panels.)
Of these green dots, half are in the triangle of interest, so:
$$\text{Corners visited twice} = \frac12\left(\frac{\mathrm{lcm}(m-1,n-1)}{m-1}-1\right)\left(\frac{\mathrm{lcm}(m-1,n-1)}{n-1}-1\right)$$
Putting it together
We can now put the two parts together to get:
$$\text{Distinct corners visited} = \mathrm{lcm}(m-1,n-1)+1 - \frac12\left(\frac{\mathrm{lcm}(m-1,n-1)}{m-1}-1\right)\left(\frac{\mathrm{lcm}(m-1,n-1)}{n-1}-1\right)$$
And we have solved the problem.
Example
For the \(4\times6\) rectangle given, our formula gives:
$$\text{Distinct corners visited} = \mathrm{lcm}(3,5)+1 - \frac12\left(\frac{\mathrm{lcm}(3,5)}{3}-1\right)\left(\frac{\mathrm{lcm}(3,5)}{5}-1\right)$$
$$= 15+1 - \frac12(5-1)(3-1)$$
$$= 16 - 4 = 12$$
This is correct:
Disproving the conjecture
In Gaurish's most recent post, he gave the following
conjecture:
The highest common factor (or greatest common divisor) of \(m\) and \(n\) always divides the number of coloured squares.
After trying to prove this for a while, I found that me attempted proof
required that \(\mathrm{hcf}(n-1,m-1)^2-1\) is a multiple of \(\mathrm{hcf}(n,m)\).
However this is not in general true (eg. 15,5).
In fact, 15,5 provides us with a counterexample to the conjecture:
![](javascript:showlimage("cross_5_15.png"))
In this diagram, 26 squares are coloured. However \(\mathrm{hcf}(15,5)=5\)
and 5 is not a factor of 26.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment