Blog
2024-12-22
I showed off and part-solved a prototype version of this puzzle with Katie Steckles in the fifteenth Finite Group livestream.
You can watch a recording of this stream, and watch our future streams if you sign up to
our Patreon.
I clearly haven't already made enough Christmas puzzles this year, so I've made another one. If you've used regular expressions before, head straight to
mscroggs.co.uk/regexmas to try the puzzle. If you've not, read on...
What is a regular expression
Regular expressions are strings of characters that can be used in multiple programming languages to validate text.
Regular expressions are usually written between two
/ characters. Between the slashes, characters have the following meaning:^(not inside square brackets) means the start of the text.$means the end of the text.- A set of characters are written between
[and]means any of these characters.
For example, the regular expression - A set of characters are written between
[^and]means any character except one of these. For example, the regular expression/^[^df]$/matches any character except d or f. ?means the previous item may or may not appear. For example, the regular expression/^ab?c$/matches "ac" or "abc".+means the previous item can appear one or more times. For example, the regular expression/^ab+c$/matches "abc", "abbc", "abbbc", and so on.*means the previous item can appear zero or more times. For example, the regular expression/^ab*c$/matches "ac", "abc", "abbc", and so on.{and}with a number between means the previous item can appear this number of times. For example, the regular expression/^ab{4}c$/matches "abbbbc".|means either the stuff to the left or the stuff to the right. For example, the regular expression/^ab|c$/matches "ab" or "c"..means any character. For example, the regular expression/^ab|.$/matches "ab" or any single character.(and)can be used to group together other symbols. Groups in brackets can be later referred to by writing\1,\2, etc to refer to the first, second, etc bracketed group. For example, the regular expression/^(a|b)\1$/matches "aa" or "bb".
/^[abc]$/ matches "a", "b", or "c".
The puzzle
My regular expression Christmas puzzle is shown below. You can either solve it on this page or at mscroggs.co.uk/regexmas
using the buttons or your keyboard, or you can download
this PDF of the puzzle.
In the grid below, write r, g, b, c, m, y, k, or w in every square so that:
- each row (reading left to right) satisfies the regular expression to the right of the row;
- each column (reading top to bottom) satisfies the regular expression below the column.
The squares containing an r will be coloured red,
those containing a g will be coloured green,
those containing a b will be coloured blue,
those containing a c will be coloured cyan,
those containing an m will be coloured magenta,
those containing a y will be coloured yellow,
those containing a k will be coloured black, and those containing a w will be left white.
/^w+yw+$/
/^([kw]+)[^kw]\1$/
/^(g|wwwg|gww)+.$/
/^wy?g*y+w+$/
/^((w|gg)(ww|g)){3}$/
/^[wg](w|g)[gw](.)\2+\1{2}$/
/^.g*[^y]$/
/^([gk][gk][gk])\1\1$/
/^yw+kw+y$/
/^w*b(bb)+w*$/
/^(w+)w?(bb?)\2\2\1$/
/^(www|bbb)+$/
/^w+gyw+$/
/^[wg]*y[wg]*$/
/^.*gwg.*gwb.*$/
/^[^g]+g+[^g]+$/
/^y?g+y?g+k?b+$/
/^[w]+g*w[^w]+$/
/^w+g+wg+[^g]+$/
/^w*yw*g+w*$/
/^w*y?g?y?w*$/
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2024-02-20
Back in November, I wrote about making 2n-page zines.
Thanks to some conversations I had at Big MathsJam
in later November, I've been able to work out how many 128-page zines there are: 315434.
The insight
At Big MathsJam, Colin Beveridge pointed out
something he'd noticed about the possible zines: when drawing the line connecting the pages
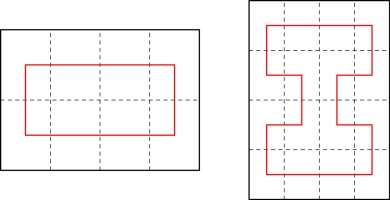
in order, there were some line segments that were always included. For example, here are all of the possible
64-page zines:
![](javascript:showlimage("64zines.png"))
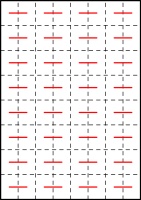
Every single one of these includes these line segments:
![](javascript:showlimage("64zines-always.png"))
Colin conjectured that for a zine of any size, a pattern like this of alternative horizontal segments
must always be included. He was close to justifying this, and since MathsJam I've been able to fill
in the full justificication.
The justificiation
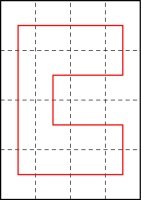
First, consider the left-most column of pages. They must be connected like this:
![](javascript:showlimage("64zines-leftcol.png"))
If they were connected in any other way, there would be two vertical connections in a row,
which would create a page that is impossible to open (as every other connection must be a horizontal
that ends up in the spine). Additionally, the horizontal lines in this diagram must all be in the
spine (as otherwise we again get pages that cannot be opened).
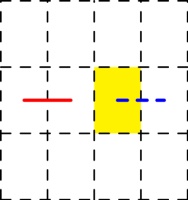
Next, consider a horizontal line that's in the spine (shown in red below), and we can look
at all the possible ways to draw the line through the highlighted page, paying particular
attention to the dashed blue line:
![](javascript:showlimage("64zines-highlighted.png"))
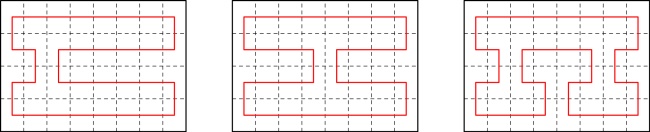
The six possible ways in which the line could travel through the highlighted page are:
![](javascript:showlimage("64zines-options.png"))
The three options in the top row do not give a valid zine: the leftmost diagram has two vertical
connections in a row (leading to pages that do not open). The other two diagrams in the top row
have the horizontal line that we know is in the spine, followed by a horizontal line not in the
spine, then a vertial line: this vertical line should be in the spine, but as it is vertical
it cannot be (without making a page that doesn't open).
In each of the diagrams in the bottom row, the connection shown in dashed blue
is included and must be in the spine: in the leftmost diagram, the horizontal line that we know is in the spine
is followed by a horizontal not in the spine, then the horizinal in the dashed blue position
that must therefore be in the spine. The othe other two diagrams in the bottom row,
the dashed blue position is connected to a vertical line: this means that the dashed blue connection
must be in the spine (as otherwise the vertical would cause a page that doesn't open).
Overall, we've now shown that the leftmost column of lines must always be included and
must all be in the spine; and for each horizontal line in the spine, the line to the right of it
after a single gap must also be included and in the spine. From this, it follows that all the horizontal
lines in Colin's pattern must always be included.
Calculating the number of 128-page zines
Now that I knew that all these horizonal lines are always included, I was able to update
the code I was using to find all the possible zines
to use this. After a few hours, it had found all 315434 possibilites. I was very happy to get this
total, as it was the same as the number that
Luna (another attendee of Big MathsJam) had calculated but wasn't certain was correct.
The sequence of the number of 2n-page zines,
including the newly calculated number,
is now published on the OEIS.
I think calculating number of 256-page zines is still beyond my code though...
×8 ×5 ×5 ×8(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2023-11-03
I showed off an unfinished version of the content in this blog post in the first
Finite Group live stream in October. I'll be showing off other upcoming things and other
content at future Finite Group events. If you'd like to watch this, you can sign up to our Patreon at
finitegroup.co.uk.
A few months ago at Cheltenham Science Festival, Hana Ayoob showed me how to make an 8-page zine.
If you've not make one before, I recommend following these steps now.
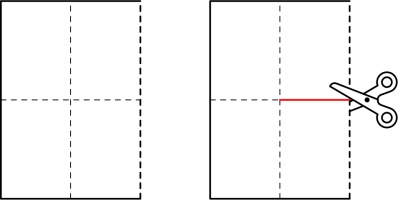
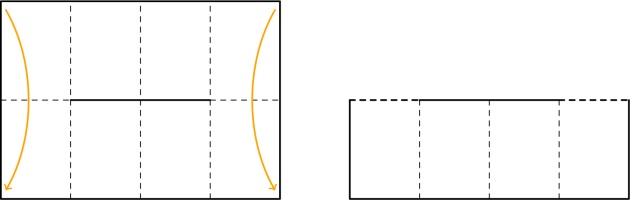
Take a piece of A4 paper, and fold it 3 times like this:
![](javascript:showlimage("8zine1.png"))
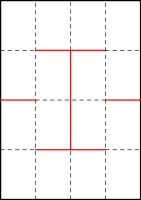
Unfold all the folds except the first one and cut along the red line:
![](javascript:showlimage("8zine2.png"))
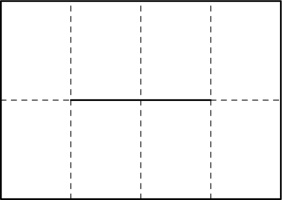
After unfolding, your paper should look like this:
![](javascript:showlimage("8zine3.png"))
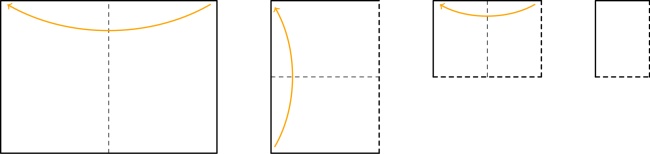
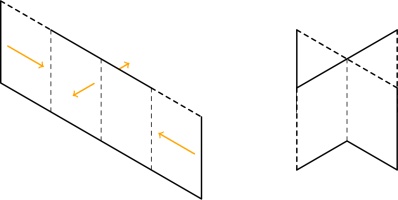
Fold the paper in half the other way:
![](javascript:showlimage("8zine4.png"))
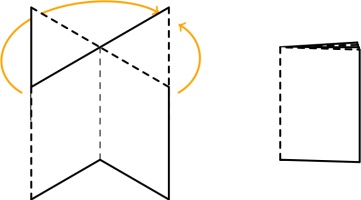
Push the two ends of the paper together so that the front of the middle bit of paper comes forward,
and the back goes backward:
![](javascript:showlimage("8zine5.png"))
Finally, flatten all the pages and you have your zine:
![](javascript:showlimage("8zine6.png"))
You're now free to write or draw whatever you like on the 8 pages of your zine.
If you'd like to fold a zine that already has content printed on it, you can
print the instructions for the TMiP puzzle hunt that I wrote earlier this year, or you can print this blog post off in zine format.
A 16-page zine
If you're anything like me, you'll already be wondering if it's possible to do some more folding
and cutting to make a 16-page zine from a piece of A4. After some trial and error, I found that
you can if you fold the paper 4 times then cut along these red lines:
![](javascript:showlimage("16zine1.png"))
(This time, I've drawn the diagram with a portrait piece of paper, as this leads to a portrait zine. For an 8-page zine, a landscape piece of paper led to a portrait zine.)
Instead of drawing which lines we need to cut, we can represent our two zines so far by drawing
lines that connect the pages in order:
![](javascript:showlimage("8and16zines.png"))
During my experimentation, I saw that every second connection between pages must be horizontal.
These horizontal connections end up in the spine of the zine and allow the pages to turn.
If you can't visualise why the pages won't turn if this condition doesn't hold, try making a 16-page
zine like this:
![](javascript:showlimage("failed16zine.png"))
32-page zines
Now that we can make a 16-page zine, the obvious question is: can we make a 32-page zine?
To answer this, we need to look for lines that go through all
32 pages where every second connection is a horizontal. I wrote a Python script to look for these and it
found 3:
![](javascript:showlimage("32zines.png"))
The code also told me that the 8- and 16-page zines we know about are the only 8- and 16-page
zines. I'm only counting the zines where the pages in the final zine are portrait, and have the same side ratio a the original piece of A4 paper:
there will be other possible zines where the pages are landscape that we aren't counting.
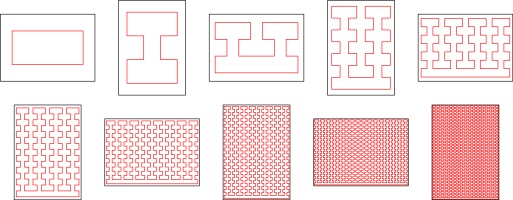
2n-page zines
Now that we have 8-page, 16-page, and 32-page zines, we can look for patterns that we
can generalise to make a 2n-page zine. This generalisation was the first I
came up with:
![](javascript:showlimage("2nzines.png"))
One possible 2n-page zine for n=3 to 12 (click to enlarge)
There are, of course, many other generalisations that you could come up with.
How many zines?
While working towards our generalised zine, you may have started pondering another question:
for any given n, how many different 2n-page zines can be made?
For n=2, there's only one way to make a zine (fold the paper twice).
For n=3 to 6, we've already seen that there are 1, 1, and 3 ways to make zines. The code
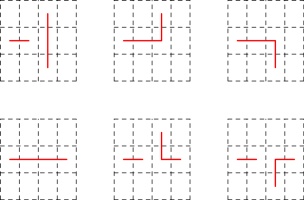
I wrote was also able to tell me that there are 31 possible 64-page zines:
All 31 possible 64-page zines (click to enlarge)
So the start of the sequence of the number of possible zines is: 1, 1, 1, 3, 31.
The number of different possible paths to check increases very quickly as we increase
n, so I was unable to compute the next term in a reasonable amount of time.
I've submitted this sequence to the OEIS. Let's
hope someone is able to work out the next term. If you're that someone, let me know!
×3 ×2 ×3 ×3 ×4(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment