Blog
2023-03-14
A circle of radius \(r\) on a piece of paper can be thought of as a line through all the points on the paper that are a distance \(r\) from the centre of the circle.
The length of this line (ie the circumference) is \(2\pi r\).
Due to the curvature of the Earth, the line through all the points that are a distance \(r\) from where you are currently standing will be less than \(2\pi r\) (although you might
not notice the difference unless \(r\) is very big). The type of curvature that a sphere has is often called positive curvature.
It is also possible to create surfaces that have negative curvature; or surfaces where the length of the line through all the points that are a distance \(r\) from a point is more than \(2\pi r\).
These surfaces are called hyperbolic surfaces.
Hyperbolic surfaces
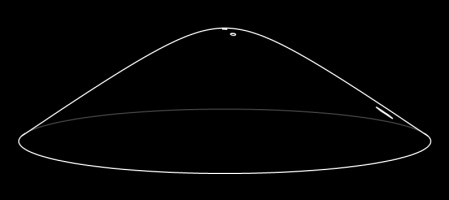
The most readily available example of a hyperbolic surface is a Pringle: Pringles are curved upwards in one direction, and curved downwards in the other direction.
![](javascript:showlimage("pringles.jpg"))
Pringles
It's not immediately obvious what a larger hyperbolic surface would look like, but you can easily make one if you know how to crochet: simply increase the number of stitches at a
constant rate.
![](javascript:showlimage("crochet-hyper.jpg"))
A hyperolic surface that I crocheted
If it was possible to continue crocheting forever, you'd get an unbounded hyperbolic surface: the hyperbolic plane.
Over the last few weeks, I've been working on adding hyperbolic levels to Mathsteroids, the asteroids-inspired game that I started making levels for in 2018.
There are quite a few different ways to represent the hyperbolic plane in 2D. In this blog post we'll take a look at some of these; I encourage you to play the Mathsteroids level for each one as you
read so that you can get a feeling for their behaviour.
Poincaré disk
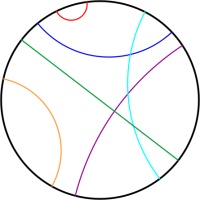
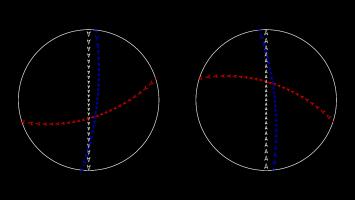
The Poincaré disk represents the hyperbolic plane as the interior of a circle. As objects move away from the centre of the circle, they appear smaller and smaller; and the circumference of
the circle is infinitely far from the centre of the circle. Straight lines on the hyperbolic plane appear on the Poincaré disk as either circles that meet the edge of the disk at right angles,
or straight lines through the centre of the circle.
![](javascript:showlimage("hyper-poincare-lines.png"))
Some examples of straight lines represented on the Poincaré disk
One of the nicest properties of the Poincaré disk is that it correctly represents angles: If you measure the angle between to intersecting straight lines represented on the disk, then the value
you measure will be the same as the angles between the two lines in the actual hyperbolic plane.
This representation can be used to demonstrate some interesting properties of the hyperbolic plane.
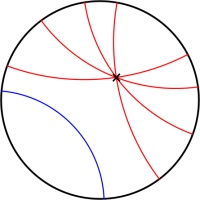
In normal two dimensional space, if you are given a line and a point then there is exactly one line that goes through the point and is parallel to the first line.
But in hyperbolic space, there are many such parallel lines.
![](javascript:showlimage("hyper-poincare-parallel.png"))
Parallel lines on the Poincaré disk: all of the red lines are parallel to the blue line
In Mathsteroids, there are two levels based on the Poincaré disk. The first level is bounded: you can only fly so far from the centre of the circle before
you hit the edge of the level and bounce back. (This prevents you from getting lost in the part of the disk where you would appear very very small.)
The second level is unbounded. In this level, you can fly as far as you like in any direction, but the point which is at the centre of the
disk will change when you go too far to prevent the ship from getting to small.
Beltrami–Klein disk
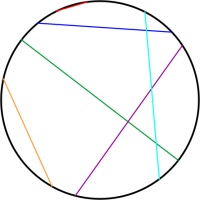
Simlar to the Poincaré disk, the Beltrami–Klein disk represents the hyperbolic plane using the interior of a circle, with the edge of the circle infinitely far away. Straight lines
in hyperbolic space will appear as straight lines in the Beltrami–Klein disk. The Beltrami–Klein disk is closely related to the Poincaré disk: the same line represented on both disks
will have its endpoints at the same points on the circle (although these endpoints are arguably not part of the line as they are on the circle that is infinitely far away).
![](javascript:showlimage("hyper-bk-lines.png"))
Some examples of straight lines represented on the Beltrami–Klein disk
Unlike in the Poincaré disk, angles are not correctly represented in the Beltrami–Klein disk. It can however be a very useful representation as straight lines appearing as straight lines
is a helpful feature.
Again, there are two Mathsteroids levels based on the Beltrami–Klein disk: a bounded level and an unbounded level.
Poincaré half-plane
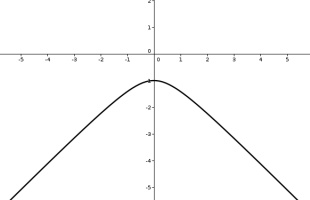
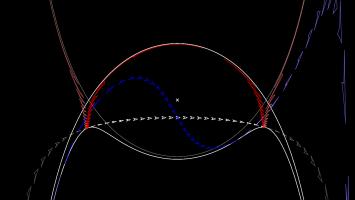
The Poincaré half-plane represents the hyperbolic plane using the half-plane above the \(x\)-axis. Straight lines in hyperbolic space are represented by either vertical
straight lines or semicircles with their endpoints on the \(x\)-axis.
![](javascript:showlimage("hyper-php-lines.png"))
Some examples of straight lines represented on the Poincaré half-plane
Like the Poincaré disk, the Poincaré half-plane correctly represents the angles between lines.
There is one Mathsteroids level based on the Poincaré half-plane: this level is bounded so you can only travel so far away from where you start.
Band
The band representation represents the hyperbolic plane as the strip between two horizontal lines. The strip extends forever to the left and right.
Straight lines on the band come in a variety of shapes.
![](javascript:showlimage("hyper-band-lines.png"))
Some examples of straight lines represented on the band
There is one Mathsteroids level based on the band representation: the bounded level.
Hyperboloid and Gans plane
The hyperbolic plane can be represented on the surface of a hyperboloid. A hyperboloid is the shape you get if you rotate and hyperbola (a curve shaped like \(y=1/x\).)
![](javascript:showlimage("hyperbola.png"))
A hyperbola
![](javascript:showlimage("hyperboloid.png"))
A hyperboloid
Straight lines on this representation are the intersections of the hyperboloid with flat planes that go through the origin.
You can see what these straight lines look like by playing the (bounded) Mathsteroids level based on the hyperboloid.
The Gans plane is simply the hyperboloid viewed from above. There is a (bounded) Mathsteroids level based on the Gans plane.
×3 ×3 ×3 ×3 ×3(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-07-06
This is a post I wrote for round 1 of The Aperiodical's Big Internet Math-Off 2018, where Mathsteroids lost to MENACE.
A map projection is a way of representing the surface of a sphere, such as the Earth, on a flat surface. There is no way to represent all the features of a sphere on a flat surface, so if you want a map that shows a certain feature of the world, then you map will have to lose some other feature of the world in return.
To show you what different map projections do to a sphere, I have created a version of the game Asteroids on a sphere. I call it Mathsteroids. You can play it here, or follow the links below to play on specific projections.
Mercator projection
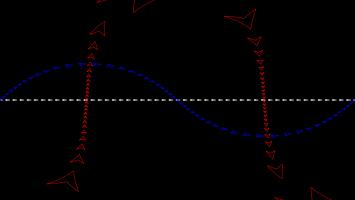
The most commonly used map projection is the Mercator projection, invented by Gerardus Mercator in 1569. The Mercator projection preserves angles: if two straight lines meet at an angle \(\theta\) on a sphere, then they will also meet at an angle \(\theta\) on the map. Keeping the angles the same, however, will cause the straight lines to no longer appear straight on the map, and the size of the same object in two different place to be very different.
The angle preserving property means that lines on a constant bearing (eg 030° from North) will appear straight on the map. These constant bearing lines are not actually straight lines on the sphere, but when your ship is already being buffeted about by the wind, the waves, and the whims of drunken sailors, a reasonably straight line is the best you can expect.
The picture below shows what three ships travelling in straight lines on the sphere look like on a Mercator projection.
![](javascript:showlimage("sphere--Mercator.png"))
To fully experience the Mercator projection, you can play Mathsteroids in Mercator projection mode here. Try flying North to see your spaceship become huge and distorted.
Gall–Peters projection
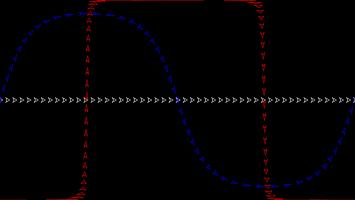
The Gall–Peters projection (named after James Gall and Arno Peters) is an area-preserving projection: objects on the map will have the same area as objects on the sphere, although the shape of the object on the projection can be very different to its shape on the sphere.
The picture below shows what three spaceships travelling in straight lines on a sphere look like on the Gall–Peters projection.
![](javascript:showlimage("sphere--Gall.png"))
You can play Mathsteroids in Gall–Peters projection mode here. I find this one much harder to play than the Mercator projection, as the direction you're travelling changes in a strange way as you move.
Azimuthal projection
![](javascript:showlimage("UNemblem.png"))
The emblem of the UN
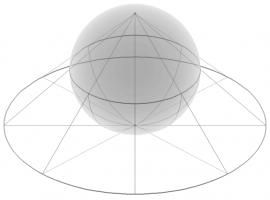
An azimuthal projection makes a map on which the directions from the centre point to other points on the map are the same as the directions on the sphere. A map like this could be useful if, for example, you're a radio operator and need to quickly see which direction you should point your aerial to communicate with other points on the map.
The azimuthal projection I've used in Mathsteroids also preserves distances: the distance from the centre to the another points on the map is proportional to the actual distance on the sphere. This projection is used as the emblem of the UN.
The picture below shows three straight lines on this projection. You can play Mathsteroids in azimuthal mode here.
![](javascript:showlimage("sphere--azim.png"))
Craig retroazimuthal projection
A retroazimuthal projection makes a map on which the directions to the centre point from other points on the map are the same as the directions on the sphere. If you're thinking that this is the same as the azimuthal projection, then you're too used to doing geometry on flat surfaces: on a sphere, the sum of the angles in a triangle depends on the size of the triangle, so the directions from A to B and from B to A aren't as closely related as you would expect.
The Craig retroazimuthal projection was invented by James Ireland Craig in 1909. He used Mecca as his centre point to make a map that shows muslims across the world which direction they should face to pray.
The picture below shows what three spaceships travelling in a straight lines on a sphere looks like on this projection.
![](javascript:showlimage("sphere--Craig.png"))
You can play Mathsteroids in Craig retroazimuthal mode here to explore the projection yourself. This is perhaps the hardest of all to play, as (a) two different parts of the sphere overlap on the map, and (b) the map is actually infinitely tall, so quite a bit of it is off the edge of the visible game area.
Stereographic projection
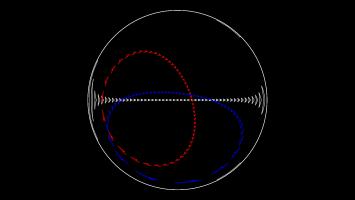
The final projection I'd like to show you is the stereographic projection.
Imagine that a sphere is sitting on a 2D plane. Take a point on the sphere. Imagine a straight line through this point and the point at the top of the sphere. The point where this line meets the 2D plane is stereographic projection of the point on the sphere.
![](javascript:showlimage("stereographic3D.png"))
The stereographic projection
This projection (backwards) can be used to represent the every complex number as a point on a sphere: this is called the Riemann sphere.
To make Mathseteroids playable after this projection, I split the sphere into 2 hemisphere and projected each seperately to give two circles. You can play Mathsteroids in stereographic projection mode here. Three spaceships travelling in straight lines on this projection are shown below.
![](javascript:showlimage("sphere--stereographic.png"))
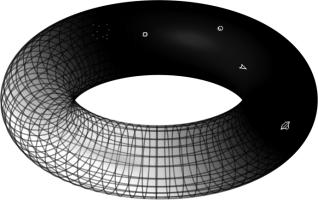
... and if you still don't like map projections, you can still enjoy playing Mathsteroids on an old fashioned torus. Or on a Klein bottle or the real projective plane. Don't forget to take a short break from playing to head over to The Aperiodical and vote (voting now closed).
×6 ×5 ×4 ×4 ×5(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-12-23
In many early arcade games, the size of the playable area was limited by the size of the screen. To make this area seem larger, or to
make gameplay more interesting, many games used wraparound; allowing the player to leave one side of the screen and return on another.
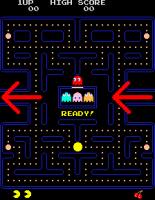
In Pac-Man, for example, the player could leave the left of the screen along the arrow shown and return
on the right, or vice versa.
![](javascript:showlimage("pac-arrows.png"))
Pac-Man's apparent teleportation from one side of the screen to the other may seem like magic, but it is more easily explained by
the shape of Pac-Man's world being a cylinder.
![](javascript:showlimage("pac-cylinder.png"))
Rather than jumping or teleporting from one side to the other, Pac-Man simply travels round the cylinder.
Bubble Bobble was first released in 1986 and features two dragons, Bub and Bob, who are tasked with
rescuing their girlfriends by trapping 100 levels
worth of monsters inside bubbles. In these levels, the dragons and monsters may leave the bottom of the screen to return at the top.
Just like in Pac-Man, Bub and Bob live on the surface of a cylinder, but this time it's horizontal not vertical.
![](javascript:showlimage("bubbob-flat.png"))
![](javascript:showlimage("bubbob-cylinder.png"))
A very large number of arcade games use left-right or top-bottom wrapping and have the same cylindrical shape as Pac-Man or Bubble Bobble.
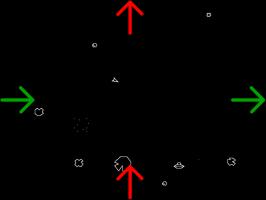
In Asteroids, both left-right and top-bottom wrapping are used.
![](javascript:showlimage("asteroids-arrows.png"))
The ships and asteroids in Asteroids live on the surface of a torus, or doughnut: a cylinder around to make its two ends meet up.
![](javascript:showlimage("asteroids-torus.png"))
There is, however, a problem with the torus show here. In Asteroids, the ship will take amount of time to get from the left of the screen
to the right however high or low on the screen it is. But the ship can get around the inside of the torus shown faster than it can
around the outside, as the inside is shorter. This is because the screen of play is completely flat, while the inside and outside halves of
the torus are curved.
It is impossible to make a flat torus in three-dimensional space, but it is possible to make one in
four-dimensional space.
Therefore, while Asteroids seems to be a simple two-dimensional game, it is actually taking place on a four-dimensional surface.
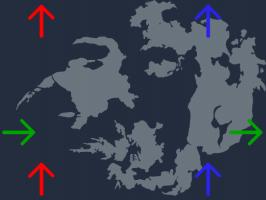
Wrapping doesn't only appear in arcade games. Many games in the excellent Final Fantasy series use wrapping on the world maps, as shown here
on the Final Fantasy VIII map.
![](javascript:showlimage("ff8-arrows.png"))
Just like in Asteroids, this wrapping means that Squall & co. carry out their adventure on the surface of a four-dimensional flat torus.
The game designers, however, seem to not have realised this, as shown in this screenshot including a spherical (!) map.
![](javascript:showlimage("ff8-sphere.png"))
Due to the curvature of a sphere, lines that start off parallel eventually meet. This makes it impossible to map
nicely between a flat surface to a sphere (this is why so many different map projections exist), and heavily complicates the task of making
a game with a truly spherical map. So I'll let the Final Fantasy VIII game designers off. Especially since the rest of the game is such
incredible fun.
It is sad, however, that there are no games (at leat that I know of) that make use of the great variety of different wrapping rules available. By only
slightly adjusting the wrapping rules used in the games in this post, it is possible to make games on a variety of other surfaces,
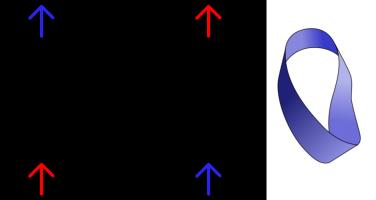
such a Klein bottles or Möbius strips as shown below.
![](javascript:showlimage("mobius-video-game.png"))
![](javascript:showlimage("klein-video-game.png"))
If you know of any games make use of these surfaces, let me know in the comments below!
×1 ×1 ×1 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
HyperRogue also has special modes which experiment with other geometries (spherical, and elliptic which is non-orientable). Hydra Slayer has Mobius strip and Klein bottle levels.×1 ×1 ×1
Zeno Rogue
×1 ×1 ×1 HyperRogue is an example of a game that takes place on the hyperbolic plane. Rather than looping, the map is infinite.
See: http://zenorogue.blogspot.com.au/2012/...
See: http://zenorogue.blogspot.com.au/2012/...
maetl
Hyperrogue may be the only game in existence with a hyperbolic surface topology: http://www.roguetemple.com/z/hyper/
zaratustra
F-Zero GX had a track called Mobius Ring, that was... well, a Möbius ring.
F-Zero X had a more trivial track that was just the outward side of a regular ring, but it was rather weird too, because it meant that this was a looping track that had no turns.
F-Zero X had a more trivial track that was just the outward side of a regular ring, but it was rather weird too, because it meant that this was a looping track that had no turns.
Olaf
Add a Comment