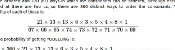Blog
Pointless probability
2013-12-15
Last week, I was watching Pointless and began wondering how likely it is that a show features four new teams.
On the show, teams are given two chances to get to the final—if they are knocked out before the final round on their first appearance, then they return the following episode. In all the following, I assumed that there was an equal chance of all teams winning.
If there are four new teams on a episode, then one of these will win and not return and the other three will return. Therefore the next episode will have one new team (with probability 1). If there are three new teams on an episode: one of the new teams could win, meaning two teams return and two new teams on the next episode (with probability 3/4); or the returning team could win, meaning that there would only one new team on the next episode. These probabilities, and those for other numbers of teams are shown in the table below:
| No of new teams today | |||||
Noof new teams tomorrow
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 0 | \(\frac{1}{4}\) | 1 | |
| 2 | 0 | \(\frac{1}{2}\) | \(\frac{3}{4}\) | 0 | |
| 3 | \(\frac{3}{4}\) | \(\frac{1}{2}\) | 0 | 0 | |
| 4 | \(\frac{1}{4}\) | 0 | 0 | 0 | |
Call the probability of an episode having one, two, three or four new teams \(P_1\), \(P_2\), \(P_3\) and \(P_4\) respectively. After a few episodes, the following must be satisfied:
$$P_1=\frac{1}{4}P_3+P_4$$
$$P_2=\frac{1}{2}P_2+\frac{3}{4}P_3$$
$$P_3=\frac{3}{4}P_3+\frac{1}{2}P_4$$
$$P_4=\frac{1}{4}P_1$$
And the total probability must be one:
$$P_1+P_2+P_3+P_4=1$$
These simultaneous equations can be solved to find that:
$$P_1=\frac{4}{35}$$
$$P_2=\frac{18}{35}$$
$$P_3=\frac{12}{35}$$
$$P_4=\frac{1}{35}$$
So the probability that all the teams on an episode of Pointless are new is one in 35, meaning that once in every 35 episodes we should expect to see all new teams.
Edit: This blog answered the same question in a slightly different way before I got here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment