Advent calendar 2017
Advent 2017 logic puzzle
2017's Advent calendar ended with a logic puzzle: It's nearly Christmas and something terrible has happened: Santa and his two elves have been cursed! The curse has led Santa to forget which present three children—Alex, Ben and Carol—want and where they live.
The elves can still remember everything about Alex, Ben and Carol, but the curse is causing them to lie. One of the elves will lie on even numbered days and tell the truth on odd numbered days; the other elf will lie on odd numbered days and tell the truth on even numbered days. As is common in elf culture, each elf wears the same coloured clothes every day.
Each child lives in a different place and wants a different present. (But a present may be equal to a home.) The homes and presents are each represented by a number from 1 to 9.
Here are the clues:
21
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
10
Orange hat says: "249 is my favourite number."
Orange hat says: "249 is my favourite number."
5
Red shoes says: "Alex lives at 1, 9 or 6."
Red shoes says: "Alex lives at 1, 9 or 6."
16
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
23
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
4
Blue shoes says: "495 is my favourite number."
Blue shoes says: "495 is my favourite number."
15
Blue shoes says: "Carol lives at 9, 6 or 8."
Blue shoes says: "Carol lives at 9, 6 or 8."
22
Purple trousers says: "Carol wants a factor of 294."
Purple trousers says: "Carol wants a factor of 294."
11
White shirt says: "497 is my favourite number."
White shirt says: "497 is my favourite number."
6
Pink shirt says: "Ben does not live at the last digit of 106."
Pink shirt says: "Ben does not live at the last digit of 106."
9
Blue shoes says: "Ben lives at 5, 1 or 2."
Blue shoes says: "Ben lives at 5, 1 or 2."
20
Orange hat says: "Carol wants the first digit of 233."
Orange hat says: "Carol wants the first digit of 233."
1
Red shoes says: "Alex wants 1, 2 or 3."
Red shoes says: "Alex wants 1, 2 or 3."
24
Green hat says: "The product of the six final presents and homes is 960."
Green hat says: "The product of the six final presents and homes is 960."
17
Grey trousers says: "Alex wants the first digit of 194."
Grey trousers says: "Alex wants the first digit of 194."
14
Pink shirt says: "One child lives at the first digit of 819."
Pink shirt says: "One child lives at the first digit of 819."
3
White shirt says: "Alex lives at 2, 1 or 6."
White shirt says: "Alex lives at 2, 1 or 6."
18
Green hat says: "Ben wants 1, 5 or 4."
Green hat says: "Ben wants 1, 5 or 4."
7
Green hat says: "Ben lives at 3, 4 or 3."
Green hat says: "Ben lives at 3, 4 or 3."
12
Grey trousers says: "Alex lives at 3, 1 or 5."
Grey trousers says: "Alex lives at 3, 1 or 5."
19
Purple trousers says: "Carol lives at 2, 6 or 8."
Purple trousers says: "Carol lives at 2, 6 or 8."
8
Red shoes says: "The digits of 529 are the toys the children want."
Red shoes says: "The digits of 529 are the toys the children want."
13
Green hat says: "One child lives at the first digit of 755."
Green hat says: "One child lives at the first digit of 755."
2
Red shoes says: "Alex wants 1, 4 or 2."
Red shoes says: "Alex wants 1, 4 or 2."
24 December
Today's number is the smallest number with exactly 28 factors (including 1 and the number itself as factors).
23 December
In the song The Twelve Days of Christmas, how many presents have been given after 8 days?
22 December
22 is two times an odd number. Today's number is the mean of all the answers on days (including today) that are two times an odd number.
Clarification: You are taking the mean for answers on days that are two times an odd numbers; ie. the days are two times odd, not the answers.
21 December
The factors of 6 (excluding 6 itself) are 1, 2 and 3. \(1+2+3=6\), so 6 is a perfect number.
Today's number is the only three digit perfect number.
20 December
What is the largest number that cannot be written in the form \(10a+27b\), where \(a\) and \(b\) are nonnegative integers (ie \(a\) and \(b\) can be 0, 1, 2, 3, ...)?
19 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the products are correct. Today's number is the smallest number that can be made using the digits in the red boxes.
| × | × | = 90 | |||
| × | × | × | |||
| × | × | = 84 | |||
| × | × | × | |||
| × | × | = 48 | |||
| = 64 | = 90 | = 63 |
18 December
Today's number is the maximum number of pieces that a (circular) pancake can be cut into with 17 straight cuts.
17 December
Arrange the digits 1-9 in a 3×3 square so that every row makes a three-digit square number, the first column makes a multiple of 7 and the second column makes a multiple of 4.
The number in the third column is today's number.
| square | |||
| square | |||
| square | |||
| multiple of 7 | multiple of 4 | today's number |
16 December
There are 204 squares (of any size) in an 8×8 grid of squares. Today's number is the number of rectangles (of any size) in a 2×19 grid of squares
15 December
The string ABBAABBBBB is 10 characters long, contains only A and B, and contains at least three As.
Today's number is the number of different 10 character strings of As and Bs that have at least three As.
14 December
There are 204 squares (of any size) in an 8×8 grid of squares. Today's number is the number of squares in a 13×13 grid of squares
13 December
A book has 754 pages (numbered 1 to 754: page 1 is on the left of the first double page spread, and page 754 is on the right of the final double page spread). What do the page numbers of the middle two-page spread add up to?
12 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. Today's number is the product of the numbers in the red boxes.
| + | + | = 17 | |||
| + | + | + | |||
| + | + | = 7 | |||
| + | + | + | |||
| + | + | = 21 | |||
| = 11 | = 20 | = 14 |
11 December
Two more than today's number is the reverse of two times today's number.
10 December
How many zeros does 1000! (ie 1000 × 999 × 998 × ... × 1) end with?
9 December
Write the numbers 1 to 15 in a row. Underneath, write the same list without the first and last numbers. Continue this until you have just one number left.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||||
| etc. | ||||||||||||||
Today's number is the sum of all the numbers you have written.
8 December
The odd numbers are written in a pyramid.
| 1 | ||||
| 3 | 5 | |||
| 7 | 9 | 11 | ||
| etc. | ||||
What is the mean of the numbers in the 23rd row?
7 December
The odd numbers are written in a pyramid.
| 1 | ||||
| 3 | 5 | |||
| 7 | 9 | 11 | ||
| etc. | ||||
What is the sum of the numbers in the seventh row?
6 December
\(p(x)\) is a quadratic with real coefficients. For all real numbers \(x\),
$$x^2+4x+14\leq p(x)\leq 2x^2+8x+18$$
\(p(2)=34\). What is \(p(6)\)?
5 December
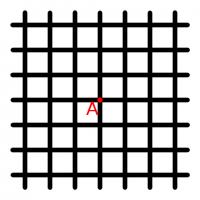
You start at A and are allow to walk left, right, up or down along the grid. The grid continues forever in every direction. After you have walked thirteen units, how many different locations could you be in?
4 December
Pick a three digit number whose digits are all different.
Sort the digits into ascending and descending order to form two new numbers. Find the difference between these numbers.
Repeat this process until the number stops changing. The final result is today's number.
3 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10. Today's number is the product of the numbers in the red boxes.
| + | + | = 17 | |||
| + | ÷ | × | |||
| ÷ | - | = 1 | |||
| - | × | ÷ | |||
| ÷ | - | = 0 | |||
| = 4 | = 12 | = 27 |
2 December
There are three cards; one number is written on each card. You are told that the sums of pairs of cards are 99, 83 and 102.
What is the sum of all three cards?
1 December
Today's number is the smallest three digit number such that the sum of its digits is equal to the product of its digits.