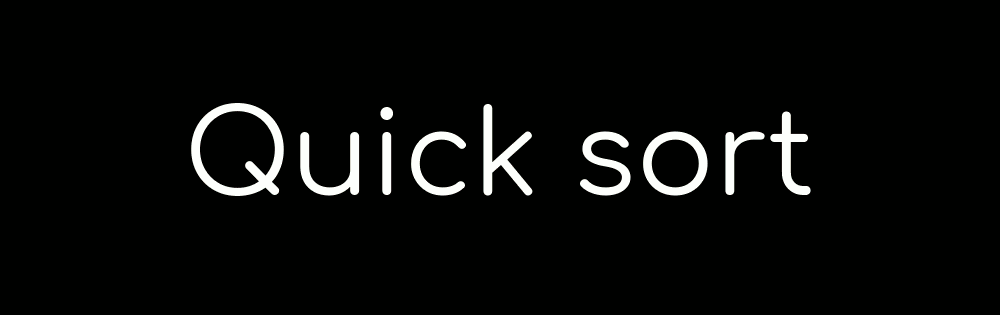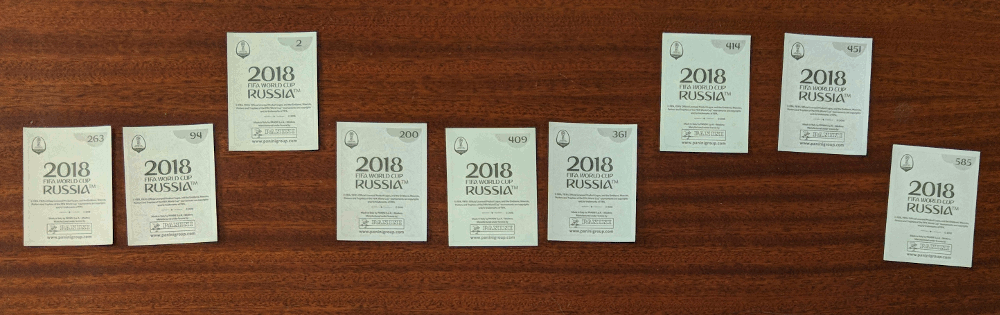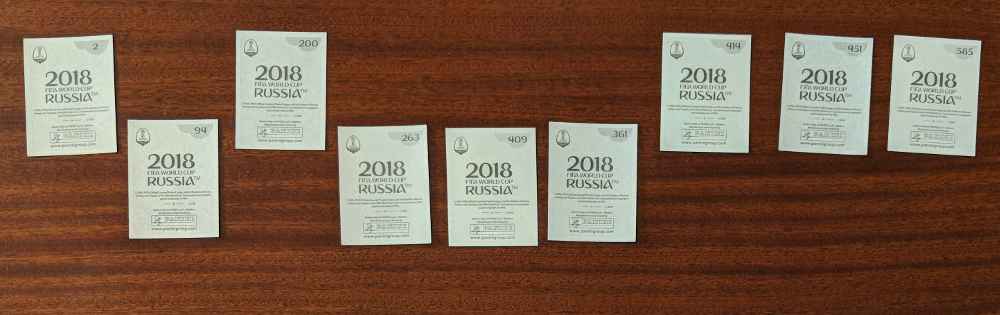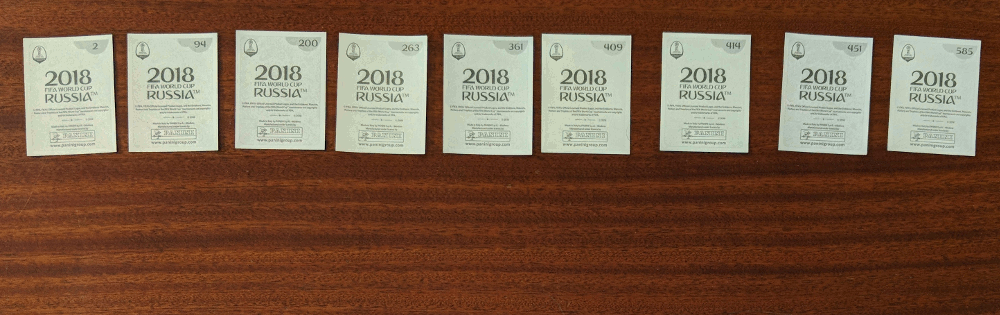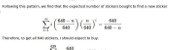Blog
2019-07-03
This year's Big Internet Math-Off
is now underway with 15 completely new contestants (plus one returning contender). As I'm not the returning contestant, I haven't been spending
my time preparing my pitches. Instead, I've spent my time making an
unofficial Big Internet Math-Off sticker book.
To complete the sticker book, you will need to collect 162 different stickers. Every day, you will be given a pack of 5 stickers; there are
also some bonus packs available if you can find them (Hint: keep reading).
How many stickers will I need?
Using the same method as I did for last year's World Cup sticker book,
you can work out that the expected number of stickers needed to finish the sticker book:
If you have already stuck \(n\) stickers into your album, then the probability that the next sticker you get is new is
$$\frac{162-n}{162}.$$
The probability that the second sticker you get is the next new sticker is
$$\mathbb{P}(\text{next sticker is not new})\times\mathbb{P}(\text{sticker after next is new})$$
$$=\frac{n}{162}\times\frac{162-n}{162}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next new sticker is
$$\left(\frac{n}{162}\right)^{i-1}\times\frac{162-n}{162}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find a new one:
$$\sum_{i=1}^{\infty}i \left(\frac{162-n}{162}\right) \left(\frac{n}{162}\right)^{i-1} = \frac{162}{162-n}$$
Therefore, to get all 162 stickers, you should expect to buy
$$\sum_{n=0}^{161}\frac{162}{162-n} = 918 \text{ stickers}.$$
Using just your daily packs, it will take you until the end of the year to collect this many stickers.
Of course, you'll only need to collect this many if you don't swap your duplicate stickers.
How many stickers will I need if I swap?
To work out the expected number of stickers stickers you'd need if you swap, let's first think about two people who want to complete
their stickerbooks together. If there are \(a\) stickers that both collectors need and \(b\) stickers that one collector has and the other one
needs, then let \(E_{a,b}\) be the expected number of stickers they need to finish their sticker books.
The next sticker they get could be one of three things:
- A sticker they both need (with probability \(\frac{a}{162}\));
- A sticker one of them needs (with probability \(\frac{b}{162}\));
- A sticker they both have (with probability \(\frac{162-a-b}{162}\)).
Therefore, the expected number of stickers they need to complete their sticker books is
$$E_{a,b}=1+\frac{a}{162}E_{a-1,b+1}+\frac{b}{162}E_{a,b-1}+\frac{162-a-b}{162}E_{a,b}.$$
This can be rearranged to give
$$E_{a,b}=
\frac{162}{a+b}+
\frac{a}{a+b}E_{a-1,b+1}
+\frac{b}{a+b}E_{a,b-1}
$$
We know that $E_{0,0}=0$ (as if \(a=0\) and \(b=0\), both collectors have already finished their sticker books). Using this and the
formula above, we can work out that
$$E_{0,1}=162+E_{0,0}=162$$
$$E_{1,0}=162+E_{0,1}=324$$
$$E_{0,2}=\frac{162}2+E_{0,1}=243$$
$$E_{1,1}=\frac{162}2+\frac12E_{0,2}+\frac12E_{1,0}=364.5$$
... and so on until we find that \(E_{162,0}=1269\), and so our collectors should expect to collect 634 stickers each to complete their
sticker books.
For three people, we can work out that if there are \(a\) stickers that all three need, \(b\) stickers that two need, and \(c\) stickers
that one needs, then
$$
E_{a,b,c}
= \frac{162}{a+b+c}+
\frac{a}{a+b+c}E_{a-1,b+1,c}
+\frac{b}{a+b+c}E_{a,b-1,c+1}
+\frac{c}{a+b+c}E_{a,b,c-1}.
$$
In the same way as for two people, we find that \(E_{162,0,0}=1572\), and so our collectors should expect to collect 524 stickers each
to complete their sticker books.
Doing the same thing for four people gives an expected 463 stickers required each.
After four people, however, the Python code I wrote to do these calculations takes too long to run, so instead I approximated the numbers
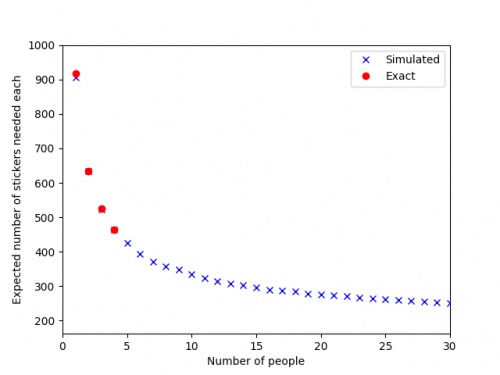
by simulating 500 groups of \(n\) people collecting stickers, and taking the average number of stickers they needed. The results are shown in
the graph below.
![](javascript:showlimage("mathoffstickerplot.png"))
The red dots are the expected values we calculated exactly, and the blue crosses are the simulated values.
It looks like you'll need to collect at least 250 stickers to finish the album: in order to get this many before the end of the Math-Off,
you'll need to find 20 bonus packs...
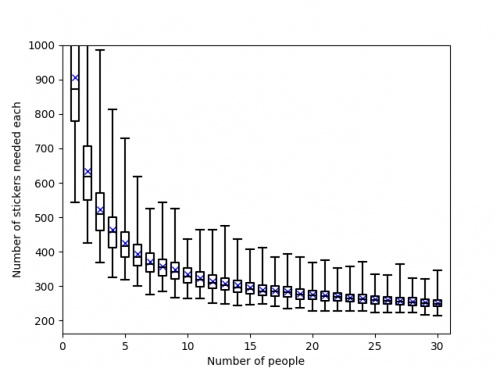
Of course, these are just the mean values and you could get lucky and need fewer stickers. The next graph shows box plots with the
quartiles of the data from the simulations.
![](javascript:showlimage("mathoffstickerboxplot.png"))
So if you're lucky, you could complete the album with fewer stickers or fewer friends.
As a thank you for reading to the end of this blog post, here's a link that
will give you two bonus packs and help you on your way to the 250 expected stickers...
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2019-07-06
@Pat Ashforth: Thanks, fixedMatthew
Link to sticker book, in the first paragraph, does not work. It points to mathoffstickbook.com
Pat Ashforth
minor typo for the 2 collector case
> and so our collectors should expect to collect 364 stickers
should be 634.
> and so our collectors should expect to collect 364 stickers
should be 634.
Road
Add a Comment
2018-07-07
So you've calculated how much you should expect the World Cup sticker book to cost
and recorded how much it actually cost. You might be wondering what else you can do with your sticker book.
If so, look no further: this post contains 5 mathematical things involvolving your sticker book and stickers.
Test the birthday paradox
![](javascript:showlimage("birthdaysbrazil.jpg"))
Stickers 354 and 369: Alisson and Roberto Firmino
In a group of 23 people, there is a more than 50% chance that two of them will share a birthday. This is often called the birthday paradox, as the number 23 is surprisingly small.
Back in 2014 when Alex Bellos suggested testing the birthday paradox on World Cup squads, as there are 23 players in a World Cup squad. I recently discovered that even further back in 2012, James Grime made a video about the birthday paradox in football games, using the players on both teams plus the referee to make 23 people.
In this year's sticker book, each player's date of birth is given above their name, so you can use your sticker book to test it out yourself.
Kaliningrad
![](javascript:showlimage("kaliningrad.jpg"))
Sticker 022: Kaliningrad
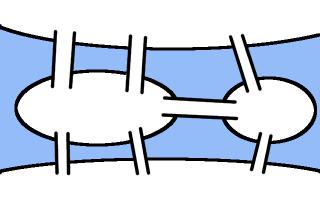
One of the cities in which games are taking place in this World Cup is Kaliningrad. Before 1945, Kaliningrad was called Königsberg. In Königsburg, there were seven bridges connecting four islands. The arrangement of these bridges is shown below.
![](javascript:showlimage("7bridges.png"))
The people of Königsburg would try to walk around the city in a route that crossed each bridge exactly one. If you've not tried this puzzle before, try to find such a route now before reading on...
In 1736, mathematician Leonhard Euler proved that it is in fact impossible to find such a route. He realised that for such a route to exist, you need to be able to pair up the bridges on each island so that you can enter the island on one of each pair and leave on the other. The islands in Königsburg all have an odd number of bridges, so there cannot be a route crossing each bridge only once.
In Kaliningrad, however, there are eight bridges: two of the original bridges were destroyed during World War II, and three more have been built. Because of this, it's now possible to walk around the city crossing each bridge exactly once.
![](javascript:showlimage("kaliningrad-path.png"))
A route around Kaliningrad crossing each bridge exactly once.
I wrote more about this puzzle, and using similar ideas to find the shortest possible route to complete a level of Pac-Man, in this blog post.
Sorting algorithms
If you didn't convince many of your friends to join you in collecting stickers, you'll have lots of swaps. You can use these to practice performing your favourite sorting algorithms.
Bubble sort
In the bubble sort, you work from left to right comparing pairs of stickers. If the stickers are in the wrong order, you swap them. After a few passes along the line of stickers, they will be in order.
![](javascript:showlimage("bubble-sort-stickers.gif"))
Bubble sort
Insertion sort
In the insertion sort, you take the next sticker in the line and insert it into its correct position in the list.
![](javascript:showlimage("insertion-sort-stickers.gif"))
Insertion sort
Quick sort
In the quick sort, you pick the middle sticker of the group and put the other stickers on the correct side of it. You then repeat the process with the smaller groups of stickers you have just formed.
![](javascript:showlimage("quick-sort-stickers.gif"))
Quick sort
The football
![](javascript:showlimage("correct-football.jpg"))
Sticker 007: The official ball
Sticker 007 shows the official tournament ball. If you look closely (click to enlarge), you can see that the ball is made of a mixture of pentagons and hexagons. The ball is not made of only hexagons, as road signs in the UK show.
Stand up mathematician Matt Parker started a petition to get the symbol on the signs changed, but the idea was rejected.
If you have a swap of sticker 007, why not stick it to a letter to your MP about the incorrect signs as an example of what an actual football looks like.
Psychic pets
Speaking of Matt Parker, during this World Cup, he's looking for psychic pets that are able to predict World Cup results. Why not use your swaps to label two pieces of food that your pet can choose between to predict the results of the remaining matches?
![](javascript:showlimage("timber-football1.jpg"))
![](javascript:showlimage("timber-football2.jpg"))
Timber using my swaps to wrongly predict the first match
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@Matthew: Thank you for the calculations. Good job I ordered the stickers I wanted #IRN. 2453 stickers - that's more than the number you bought (1781) to collect all stickers!
Milad
@Matthew: Here is how I calculated it:
You want a specific set of 20 stickers. Imagine you have already \(n\) of these. The probability that the next sticker you buy is one that you want is
$$\frac{20-n}{682}.$$
The probability that the second sticker you buy is the next new sticker is
$$\mathbb{P}(\text{next sticker is not wanted})\times\mathbb{P}(\text{sticker after next is wanted})$$
$$=\frac{662+n}{682}\times\frac{20-n}{682}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next wanted sticker is
$$\left(\frac{662+n}{682}\right)^{i-1}\times\frac{20-n}{682}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find the next wanted one:
$$\sum_{i=1}^{\infty}i \left(\frac{20-n}{682}\right) \left(\frac{662+n}{682}\right)^{i-1} = \frac{682}{20-n}$$
Therefore, to get all 682 stickers, you should expect to buy
$$\sum_{n=0}^{19}\frac{682}{20-n} = 2453 \text{ stickers}.$$
You want a specific set of 20 stickers. Imagine you have already \(n\) of these. The probability that the next sticker you buy is one that you want is
$$\frac{20-n}{682}.$$
The probability that the second sticker you buy is the next new sticker is
$$\mathbb{P}(\text{next sticker is not wanted})\times\mathbb{P}(\text{sticker after next is wanted})$$
$$=\frac{662+n}{682}\times\frac{20-n}{682}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next wanted sticker is
$$\left(\frac{662+n}{682}\right)^{i-1}\times\frac{20-n}{682}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find the next wanted one:
$$\sum_{i=1}^{\infty}i \left(\frac{20-n}{682}\right) \left(\frac{662+n}{682}\right)^{i-1} = \frac{682}{20-n}$$
Therefore, to get all 682 stickers, you should expect to buy
$$\sum_{n=0}^{19}\frac{682}{20-n} = 2453 \text{ stickers}.$$
Matthew
@Matthew: Yes, I would like to know how you work it out please. I believe I have left my email address in my comment. It seems like a lot of stickers if you are just interested in one team.
Milad
@Milad: Following a similiar method to this blog post, I reckon you'd expect to buy 2453 stickers (491 packs) to get a fixed set of 20 stickers. Drop me an email if you want me to explain how I worked this out.
Matthew
Thanks for the maths, but I have one probability question. How many packs would I have to buy, on average, to obtain a fixed set of 20 stickers?
Milad
Add a Comment
2018-06-16
This year, like every World Cup year, I've been collecting stickers to fill the official Panini World Cup sticker album.
Back in March, I calculated that I should expect it to cost £268.99 to fill this year's album (if I order the last 50 stickers).
As of 6pm yesterday, I need 47 stickers to complete the album (and have placed an order on the Panini website for these).
So... How much did it cost?
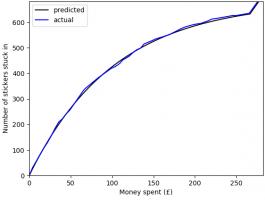
In total, I have bought 1781 stickers (including the 47 I ordered) at a cost of £275.93. The plot below shows
the money spent against the number of stickers stuck in, compared with the what I predicted in March.
![](javascript:showlimage("panini2018plot1.png"))
To create this plot, I've been keeping track of exactly which stickers were in each pack I bought. Using this data, we can
look for a few more things. If you want to play with the data yourself, there's a link at the bottom to download it.
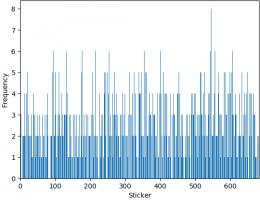
Swaps
The bar chart below shows the number of copies of each sticker I got (excluding the 47 that I ordered). Unsurprisingly, it looks a lot like
random noise.
![](javascript:showlimage("panini2018plot3.png"))
The sticker I got most copies of was sticker 545, showing Panana player Armando Cooper.
![](javascript:showlimage("sticker545.jpg"))
Armando Cooper on sticker 545
I got swaps of 513 different stickers, meaning I'm only 169 stickers short of filling a second album.
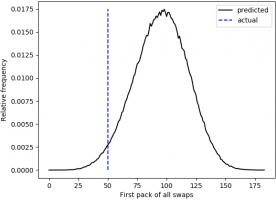
First pack of all swaps
Everyone who has every done a sticker book will remember the awful feeling you get when you first get a pack of all swaps.
For me, the first time this happened was the 50th pack. The plot below shows when the first pack of all swaps occurred in 500,000 simulations.
![](javascript:showlimage("panini2018plot2.png"))
Looks like I was really quite unlucky to get a pack of all swaps so soon.
Duplicates in a pack
In all the 345 packs that I bought, there wasn't a single pack that contained two copies of the same sticker.
In fact, I don't remember ever getting two of the same sticker in a pack. For a while I've been wondering if this is because Panini
ensure that packs don't contain duplicates, or if it's simply very unlikely that they do.
If it was down to unlikeliness, the probability of having no duplicates in one pack would be:
\begin{align}
\mathbb{P}(\text{no duplicates in a pack}) &= 1 \times\frac{681}{682}\times\frac{680}{682}\times\frac{679}{682}\times\frac{678}{682}\\
&= 0.985
\end{align}
and the probability of none of my 345 containing a duplicate would be:
\begin{align}
\mathbb{P}(\text{no duplicates in 345 packs})
&= 0.985^{345}\\
&= 0.00628
\end{align}
This is very very small, so it's safe to conclude that Panini do indeed ensure that packs do not contain duplicates.
The data
If you'd like to have a play with the data yourself, you can download it here. Let me know if
you do anything with it...
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-05-02
Every morning just before 7am, one of the Today Programme's presenters reads out a puzzle. Yesterday, it was this puzzle:
In a given month, the probability of a certain daily paper either running a story about inappropriate behaviour at a party conference or running one about somebody's pet being retrieved from a domestic appliance is exactly half the probability of the same paper containing a photo of a Tory MP jogging. The probability of no such photo appearing is the same as that of there being a story about inappropriate behaviour at a party conference. The probability of the paper running a story about somebody's pet being retrieved from a domestic appliance is a quarter that of its containing a photo of a Tory MP jogging. What are the probabilities the paper will (a) run the conference story, (b) run the pet story, (c) contain the jogging photo?
I'm not the only one to notice that some of Radio 4's daily puzzles are not great.
I think this puzzle is a great example of a terrible puzzle. You can already see the first problem with it: it's long and words and very hard to follow on the radio.
But maybe this isn't so important, as you can
read it here after it's been read out.
Once you've done this, you can re-write the puzzle as follows:
there are three news stories (\(A\), \(B\) and \(C\)) that the newspaper might publish in a month. We are given the following information:
$$\mathbb{P}(A\text{ or }B)=\tfrac12\mathbb{P}(C)$$
$$1-\mathbb{P}(C)=\mathbb{P}(A)$$
$$\mathbb{P}(B)=\tfrac14\mathbb{P}(C)$$
To solve this puzzle, we need use the formula \(\mathbb{P}(A\text{ or }B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\text{ and }B)\).
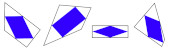
These Venn diagrams justify this formula:
![](javascript:showlimage("venn-probab.png"))
Venn diagrams showing that \(\mathbb{P}(A\text{ or }B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\text{ and }B)\).
Using the information we were given in the question, we get:
\begin{align}
\tfrac12\mathbb{P}(C)&=\mathbb{P}(A\text{ or }B)\\
&=1-\mathbb{P}(C)+\tfrac14\mathbb{P}(C)-\mathbb{P}(A\text{ and }B)\\
\mathbb{P}(C)&=\tfrac45(1-\mathbb{P}(A\text{ and }B)).
\end{align}
At this point we have reached the second problem with this puzzle: there's no answer unless we make some extra assumptions, and the question doesn't make it clear what we can assume.
But let's give the puzzle the benefit of the doubt and try some assumptions.
Assumption 1: The events are mutually exclusive
If we assume that the events \(A\) and \(B\) are mutually exclusive—or, in other words, only one of these two articles can be published,
perhaps due to a lack of space—then we can use the fact that
$$\mathbb{P}(A\text{ and }B)=0.$$
This means that
\(\mathbb{P}(C)=\tfrac45\),
\(\mathbb{P}(A)=\tfrac15\), and
\(\mathbb{P}(B)=\tfrac15\). There's a problem with this answer, though: the three probabilities add up to more than 1.
This wouldn't be a problem, except we assumed that only one of the articles \(A\) and \(B\) could be published.
The probabilities adding up to more than 1 means that either \(A\) and \(C\) are not mutually exclusive or \(A\) and \(B\) are not mutually exclusive,
so \(C\) could be published alongside \(A\) or \(B\). There seems to be nothing special about the three news stories to mean that only some combinations
could be published together, so at this point I figured that this assumption was wrong and moved on.
Today, however, the answer was posted, and
this answer was given (without an working out). So we have a third problem with this puzzle: the answer that was given is wrong, or at the very best
is based on questionable assumptions.
Assumption 2: The events are independent
If we assume that the events are independent—so one article being published doesn't affect whether or not another is published—then
we may use the fact that
$$\mathbb{P}(A\text{ and }B)=\mathbb{P}(A)\mathbb{P}(B).$$
If we let \(c=\mathbb{P}(C)\), then we get:
\begin{align}
\tfrac12c&=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\text{ and }B)\\
&=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A)\mathbb{P}(B)\\
&=1-c+\tfrac14c-\tfrac14(1-c)c\\
\tfrac14c^2-\tfrac32c+1&=0.
\end{align}
You can use your favourite formula to solve this to find that \(c=3-\sqrt5\), and therefore
\(\mathbb{P}(A)=\sqrt5-2\) and
\(\mathbb{P}(B)=\tfrac34-\tfrac{\sqrt5}4\).
In this case, our assumption appears to be more reasonable—as over the course of a month the stories published by a paper probably don't have
much of an effect on each other—but we have the fourth, and probably biggest problem with the puzzle: the question and answer are not interesting or surprising, and
the method is a bit tedious.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@Stefan: It's possible that that was intended but it's not completely clear. If that was the intention, I stick to my point that it's odd that the other story can be published alongside these two.
Matthew
Doesn’t the word ‘either’ in the opening phrase make A and B explicity exclusive?
Stefan
Add a Comment
2018-03-23
This morning, I heard about Arnie Ellis on the Today programme. Arnie is the first baby boy to be born in his family in five generations, following ten girls. According to John Humphrys, there is a 20,000-to-1 chance of this happening. Pretty quickly, I started wondering where this number came from.
After a quick Google, I found that this news story had appeared in many of today's papers, including the Sun and the Daily Mail. They all featured this 20,000-to-1 figure, which according to The Sun originally came from Ladbrokes.
What is the chance of this happening?
If someone is having a child, the probability of it being a girl is 0.5. The probability of it being a boy is also 0.5. So the probaility of having ten girls followed by a boy is
$$\left(\tfrac12\right)^{10}\times\tfrac12=\frac1{2048}.$$
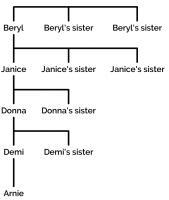
If all 11 children were siblings, then this would be the chance of this happening—and it's a long way off the 20,000-to-1. But in Arnie's case, the situation is different. Luckily in the Daily Mail article, there is an outline of Arnie's family tree.
![](javascript:showlimage("familytree.png"))
Here, you can see that the ten girls are spread over five generations. So the question becomes: given a baby, what is the probability that the child is male and his most recently born ten relatives on their mother's side are all female?
Four of the ten relatives are certainly female—Arnie's mother, grandmother, great grandmother and great great grandmother are all definitely female. This only leaves six more relatives, so the probability of a baby being in Arnie's position is
$$\left(\tfrac12\right)^{6}\times\tfrac12=\frac1{128}.$$
This is now an awful lot lower than the 20,000-to-1 we were told. In fact, with around 700,000 births in the UK each year, we'd expect over 5,000 babies to be born in this situation every year. Maybe Arnie's not so rare after all.
This number is based on the assumption that the baby's last ten relatives are spread across five generations. But the probability will be different if the relatives are spread over a different number of generations. Calculating the probability for a baby with any arrangement of ancestors would require knowing the likelihood of each arrangement of relatives, which would require a lot of data that probably doesn't exist. But the actual anwer is probably not too far from 127-to-1.
Where did 20,000-to-1 come from?
This morning, I emailed Ladbrokes to see if they could shed any light on the 20,000-to-1 figure. They haven't got back to me yet. (Although they did accidentally CC me when sending the query on to someone who might know the answer, so I'm hopeful.) I'll update this post with an explanaation if I do hear back.
Until then, there is one possible explanation for the figure: we have looked at the probability that a baby will be in this situation, but we could instead have started at the top of the family tree and looked at the probability that Beryl's next ten decendents were girls followed by a boy. The probability of this happening will be lower, as there is a reasonable chance that Beryl could have no female children, or no children at all. Looking at the problem this way, there are more ways for the situation to not happen, so the probability of it happening is lower.
But working the actually probability out in this way would again require data about how many children are likely in each generation, and would be a complicated calculation. It seems unlikely that this is what Ladbrokes did. Let's hope they shed some light on it...
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment