Blog

As a child, I was a huge fan of Captain Scarlet and the Mysterons, Gerry Anderson's puppet-starring sci-fi series. As an adult, I am still a huge fan of Captain Scarlet and the Mysterons. Set in 2068, the series follows Captain Scarlet and the other members of Spectrum as they attempt to protect Earth from the Mysterons. One of my favourite episodes of the series is the third: Big Ben Strikes Again.

In this episode, the Mysterons threaten to destroy London. They do this by hijacking a vehicle carrying a nuclear device, and driving it to a car park. In the car park, the driver of the vehicle wakes up and turns the radio on. Then something weird happens: Big Ben strikes thirteen!

Following this, the driver is knocked out again and wakes up in a side road somewhere. After hearing his story, Captain Blue works out that the car park must be 1500 yards away from Big Ben. Using this information, Captains Blue and Scarlet manage to track down the nuclear device and save the day.

After rewatching the episode recently, I realised that it would be possible to recreate this scene and hear Big Ben striking thirteen.

At the end of the episode, Captain Blue explains to Captain Scarlet that the effect was due to light travelling faster than sound: as the driver had the radio on, he could hear Ben's bongs both from the tower and through the radio. As radio waves travel faster than sound, the bongs over the radio can be heard earlier than the sound waves travelling through the air. Further from the tower, the gap between when the two bongs are heard is longer; and at just the right distance, the second bong on the radio will be heard at the same time as the first bong from the tower. This leads to the appearance of thirteen bongs: the first bong is just from the radio, the next eleven are both radio and from the tower, and the final bong is only from the tower.

Big Ben's bongs are approximately 4.2s apart, sound travels at 343m/s, and light travels at 3×10⁸m/s (this is so fast that it could be assumed that the radio waves arrive instantly without changing the answer). Using these, we perform the following calculation:

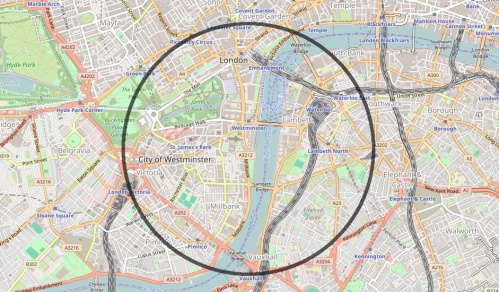
This is close to Captain Blue's calculation of 1500 yards (and to be fair to the Captain, he had to calculate it in his head in a few seconds). Plotting a circle of this radius centred at Big Ben gives the points where it may be possible to hear 13 bongs.

Again, the makers of Captain Scarlet got this right: their circle shown earlier is a very similar size to this one. To demonstrate that this does work (and with a little help from TD and her camera), I made the following video yesterday near Vauxhall station. I recommend using earphones to watch it as the later bongs are quite faint.

After my talk at Electromagnetic Field 2014, I was sent a copy of MC Escher Kaleidocycles by Doris Schattschneider and Wallace Walker (thanks Bob!). A kaleidocycle is a bit like a 3D flexagon: it can be flexed to reveal different parts of itself.

In this blog post, I will tell you how to make a kaleidocycle from tube maps.

First, fold the cover of a tube map over. This will allow you to have the tube map (and not just its cover) on the faces of your shape.

With the side you want to see facing down, fold the map so that two opposite corners touch.

For this step, there is a choice of which two corners to connect: leading to a right-handed and a left-handed piece. You should make 6 of each type for your kaleidocycle.

Finally, fold the overhanding bits over to complete your module.

The folds you made when connecting opposite corners will need to fold both ways when you flex your shape, so it is worth folding them both ways a few times now before continuing.

Once you have made 12 modules (with 6 of each handedness), you are ready to put the kaleidocycle together.

Take two tube maps of each handedness and tuck them together in a line. Each map is tucked into one of the opposite handedness.

The four triangles across the middle form a net of a tetrahedron. Complete the tetrahedron by putting the last tab into the first triangle. Glue these together.

Take two more tube maps of the opposite handedness to those at the top of the tetrahedron. Fit them into the two triangles poking out of the top of the tetrahedron to make a second tetrahedron.

Repeat this until you have five connected tetrahedra. Finally, connect the triangles poking out of the top and the bottom to make your kaleidocycle.

A while ago, I made this (a stellated rhombicuboctahedron):

Here are some hastily typed instructions for Matt Parker, who is making one at this month's Maths Jam. Other people are welcome to follow these instructions too.

First, take a tube map and fold the cover over. This will ensure that your shape will have tube (map and not index) on the outside and you will have pages to tuck your tabs between later.

Now fold one corner diagonally across to another corner. It does not matter which diagonal you chose for the first piece but after this all following pieces must be the same as the first.

Now fold the overlapping bit back over the top.

Turn it over and fold this overlap over too.

You have made one module.

You will need 48 of these and some glue.

By slotting three or four of these modules together, you can make a pyramid with a triangle or square as its base.

A stellated rhombicuboctahedron is a rhombicuboctahedron with a pyramid, or stellation on each face. In other words, you now need to build a rhombicuboctahedron with the bases of pyramids like these. A rhombicuboctahedron looks like this:

More usefully, its net looks like this:

To build a stellated rhombicuboctahedron, make this net, but with each shape as the base of a pyramid. This is what it will look like 6/48 tube maps in:

If you make on of these, please tweet me a photo so I can see it!

In 2012, I folded all the Platonic solids from tube maps. The dodecahedron I made was a little dissapointing:

After my talk at Electromegnetic Field 2014, I was shown the following better method to fold a dodecahedron.

First, take a tube map, cut apart all the pages and cut each page in half.

Next, take one of the parts and fold it into four

then lay it flat.

Next, fold the bottom left corner upwards

and the top right corner downwards.

Finally, fold along the line shown below.

You have now made a module which will make up one edge of the dodecahedron. You will need 30 of these to make the full solid.

Once many modules have been made, then can be put together. To do this, tuck one of the corners you folded over into the final fold of another module.

Three of the modules attached like this will make a vertex of the dodecahedron.

By continuing to attach modules, you will get the shell of a dodecahedron.

To make the dodecahedron look more complete, fold some more almost-squares of tube map to be just larger than the holes and tuck them into the modules.

Following my previous post, I did a little more folding.

The post was linked to on Going Underground's Blog where it received this comment:

In response to which I made this from 48 tube maps:

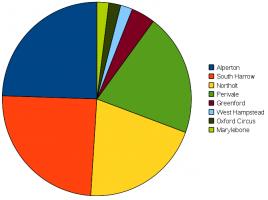
Also since the last post, I left 49 tetrahedrons at tube stations in a period of just over two weeks. Here's a pie chart showing which stations I left them at:

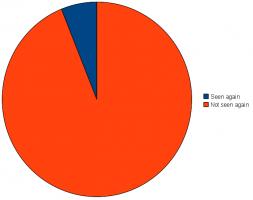
Of these 49, only three were still there the next time I passed through the station:

Due to the very low recapture rate, little more analysis can be done. Although I do wonder where they all ended up. Do you work at one of those stations and threw some away? Or did you pass through a station and pick one up? Or was it aliens and ghosts?

For my next trick, I want to gather a team of people, pick a day, and leave one at every station that day. If you want to join me, comment on this post, tweet me or comment on reddit and we can formulate a plan. Including your nearest station(s) in your message will help us sort out who takes which stations...