Blog
Christmas (2017) is over
2018-01-02
It's 2018, and the Advent calendar has disappeared, so it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, Santa was able to work out which present each child wanted, and get their presents to them just in time:
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar.
4 December
Pick a three digit number whose digits are all different.
Sort the digits into ascending and descending order to form two new numbers. Find the difference between these numbers.
Repeat this process until the number stops changing. The final result is today's number.
This puzzle revealed the surprising fact that repeatedly sorting the digits of a three digit number
into ascending and descending order then finding the difference will always give the same answer (as long as the digits of the starting number are all different).
This process is known as the Kaprekar mapping.
If four digit starting numbers are chosen, then all starting numbers that do not have three equal digits will eventually lead to 6174.
It's not as simple for five digit numbers, but I'll leave you to investigate this...
Ruben pointed something interesting out to me about this question: if you remove the constraint
that the answer must be a three digit number, then you see that the numbers 47, 497, 4997, 49997, and in fact any number of the form 49...97
will have this property.
20 December
What is the largest number that cannot be written in the form \(10a+27b\), where \(a\) and \(b\) are nonnegative integers (ie \(a\) and \(b\) can be 0, 1, 2, 3, ...)?
If you didn't manage to solve this one, I recommend trying replacing the 10 and 27 with smaller numbers (eg 3 and 4)
and solving the easier puzzle you get first, then trying to generalise the problem.
You can find my write up of this solution here.
Pedro Freitas (@pj_freitas) sent me a different way to approach this problem (related to solving the same question with different numbers on this year's Christmas card). To see his method, click "Show Answer & Extension" in the puzzle box above.
24 December
Today's number is the smallest number with exactly 28 factors (including 1 and the number itself as factors).
I really like the method I used to solve this one. To see it, click "Show Answer" above.
Solving all 24 puzzles lead to the following final logic puzzle:
Advent 2017 logic puzzle
2017's Advent calendar ended with a logic puzzle: It's nearly Christmas and something terrible has happened: Santa and his two elves have been cursed! The curse has led Santa to forget which present three children—Alex, Ben and Carol—want and where they live.
The elves can still remember everything about Alex, Ben and Carol, but the curse is causing them to lie. One of the elves will lie on even numbered days and tell the truth on odd numbered days; the other elf will lie on odd numbered days and tell the truth on even numbered days. As is common in elf culture, each elf wears the same coloured clothes every day.
Each child lives in a different place and wants a different present. (But a present may be equal to a home.) The homes and presents are each represented by a number from 1 to 9.
Here are the clues:
21
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
White shirt says: "Yesterday's elf lied: Carol wants 4, 9 or 6."
10
Orange hat says: "249 is my favourite number."
Orange hat says: "249 is my favourite number."
5
Red shoes says: "Alex lives at 1, 9 or 6."
Red shoes says: "Alex lives at 1, 9 or 6."
16
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
Blue shoes says: "I'm the same elf as yesterday. Ben wants 5, 7 or 0."
23
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
Red shoes says: "Carol wants a factor of 120. I am yesterday's elf."
4
Blue shoes says: "495 is my favourite number."
Blue shoes says: "495 is my favourite number."
15
Blue shoes says: "Carol lives at 9, 6 or 8."
Blue shoes says: "Carol lives at 9, 6 or 8."
22
Purple trousers says: "Carol wants a factor of 294."
Purple trousers says: "Carol wants a factor of 294."
11
White shirt says: "497 is my favourite number."
White shirt says: "497 is my favourite number."
6
Pink shirt says: "Ben does not live at the last digit of 106."
Pink shirt says: "Ben does not live at the last digit of 106."
9
Blue shoes says: "Ben lives at 5, 1 or 2."
Blue shoes says: "Ben lives at 5, 1 or 2."
20
Orange hat says: "Carol wants the first digit of 233."
Orange hat says: "Carol wants the first digit of 233."
1
Red shoes says: "Alex wants 1, 2 or 3."
Red shoes says: "Alex wants 1, 2 or 3."
24
Green hat says: "The product of the six final presents and homes is 960."
Green hat says: "The product of the six final presents and homes is 960."
17
Grey trousers says: "Alex wants the first digit of 194."
Grey trousers says: "Alex wants the first digit of 194."
14
Pink shirt says: "One child lives at the first digit of 819."
Pink shirt says: "One child lives at the first digit of 819."
3
White shirt says: "Alex lives at 2, 1 or 6."
White shirt says: "Alex lives at 2, 1 or 6."
18
Green hat says: "Ben wants 1, 5 or 4."
Green hat says: "Ben wants 1, 5 or 4."
7
Green hat says: "Ben lives at 3, 4 or 3."
Green hat says: "Ben lives at 3, 4 or 3."
12
Grey trousers says: "Alex lives at 3, 1 or 5."
Grey trousers says: "Alex lives at 3, 1 or 5."
19
Purple trousers says: "Carol lives at 2, 6 or 8."
Purple trousers says: "Carol lives at 2, 6 or 8."
8
Red shoes says: "The digits of 529 are the toys the children want."
Red shoes says: "The digits of 529 are the toys the children want."
13
Green hat says: "One child lives at the first digit of 755."
Green hat says: "One child lives at the first digit of 755."
2
Red shoes says: "Alex wants 1, 4 or 2."
Red shoes says: "Alex wants 1, 4 or 2."
Together the clues reveal what each elf was wearing:

Drawn by Alison Clarke

Drawn by Adam Townsend
and allow you to work out where each child lives and what they wanted. Thanks Adam and Alison for drawing the elves for me.
I had a lot of fun finding place names with numbers in them to use as answers in the final puzzle. For the presents, I used the items from The 12 Days of Christmas:
| # | Location | Present |
| 1 | Maidstone, Kent | a partridge |
| 2 | Burcot, Worcestershire | turtle doves |
| 3 | Three Holes, Norfolk | French hens |
| 4 | Balfour, Orkney | calling birds |
| 5 | Fivehead, Somerset | gold rings |
| 6 | Sixpenny Handley, Dorset | geese |
| 7 | Sevenhampton, Glos | swans |
| 8 | Leighton Buzzard, Beds | maids |
| 9 | Nine Elms, Wiltshire | ladies |
I also snuck a small Easter egg into the calendar: the doors were arranged in a knight's tour, as shown below.
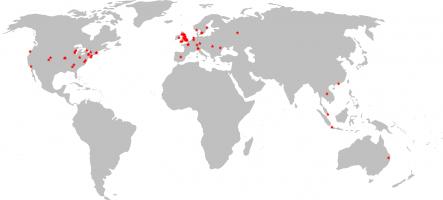
And finally (and maybe most importantly), on to the winners: 84 people submitted answers to the final logic puzzle. Their (very) approximate locations are shown on this map:
From the correct answers, the following 10 winners were selected:
| 1 | M Oostrom |
| 2 | Rosie Paterson |
| 3 | Jonathan Winfield |
| 4 | Lewis Dyer |
| 5 | Merrilyn |
| 6 | Sam Hartburn |
| 7 | Hannah Charman |
| 8 | David |
| 9 | Thomas Smith |
| 10 | Jessica Marsh |
Congratulations! Your prizes will be on their way shortly. Additionally, well done to Alan Buck, Alessandra Zhang, Alex Burlton, Alex Hartz, Alex Lam, Alexander, Alexander Bolton, Alexandra Seceleanu, Arturo, Brennan Dolson,
Carmen Günther, Connie, Dan Whitman, David Fox, David Kendel, Ed, Elijah Kuhn, Eva, Evan Louis Robinson, Felix Breton,
Fred Verheul, Henry Hung, Joakim Cronvall, Joe Gage, Jon Palin, Kai Lam, Keith Sutherland, Kelsey, Kenson Li, Koo Zhengqun,
Kristen Koenigs, Lance Nathan, Louis de Mendonca, Mark Stambaugh, Martin Harris, Martine Vijn Nome, Matt Hutton, Matthew Schulz, Max Nilsson, Michael DeLyser,
Michael Smith, Michael Ye, Mihai Zsisku, Mike Walters, Mikko, Naomi Bowler, Pattanun Wattana, Pietro Alessandro Murru, Raj, Rick,
Roni, Ross Milne, Ruben, Ryan Howerter, Samantha Duong, Sarah Brook, Shivanshi, Steve Paget, Steven Peplow, Steven Spence,
Tony Mann, Valentin Vălciu, Virgile Andreani, and Yasha Asley, who all also submitted the correct answer but were too unlucky to win prizes
this time.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment






I particularly liked the riddle on the 5th of December (with walking 13 units) - it was quite tricky at first, but then I solved it by seeing that you can't end up on a square an even distance away from the centre, so the possible areas are in "circles" from the center with odd side lengths . It was quite reminiscent of showing you can't cover a chessboard with dominoes when two opposite corners are removed .