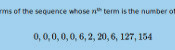Blog
2017-11-14
A few weeks ago, I took the copy of MENACE that I built to Manchester Science Festival, where it played around 300 games against the public while learning to play Noughts and Crosses. The group of us operating MENACE for the weekend included Matt Parker, who made two videos about it. Special thanks go to Matt, plus
Katie Steckles,
Alison Clarke,
Andrew Taylor,
Ashley Frankland,
David Williams,
Paul Taylor,
Sam Headleand,
Trent Burton, and
Zoe Griffiths for helping to operate MENACE for the weekend.
As my original post about MENACE explains in more detail, MENACE is a machine built from 304 matchboxes that learns to play Noughts and Crosses. Each box displays a possible position that the machine can face and contains coloured beads that correspond to the moves it could make. At the end of each game, beads are added or removed depending on the outcome to teach MENACE to play better.
Saturday
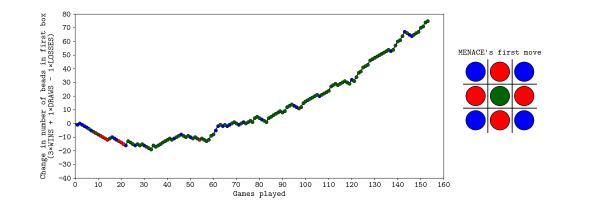
On Saturday, MENACE was set up with 8 beads of each colour in the first move box; 3 of each colour in the second move boxes; 2 of each colour in third move boxes; and 1 of each colour in the fourth move boxes. I had only included one copy of moves that are the same due to symmetry.
The plot below shows the number of beads in MENACE's first box as the day progressed.
![](javascript:showlimage("sat-same-axes.png"))
Sunday
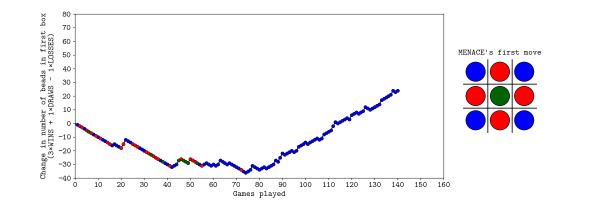
Originally, we were planning to let MENACE learn over the course of both days, but it learned more quickly than we had expected on Saturday, so we reset is on Sunday, but set it up slightly differently. On Sunday, MENACE was set up with 4 beads of each colour in the first move box; 3 of each colour in the second move boxes; 2 of each colour in third move boxes; and 1 of each colour in the fourth move boxes. This time, we left all the beads in the boxes and didn't remove any due to symmetry.
The plot below shows the number of beads in MENACE's first box as the day progressed.
![](javascript:showlimage("sun-same-axes.png"))
The data
You can download the full set of data that we collected over the weekend here. This includes the first two moves and outcomes of all the games over the two days, plus the number of beads in each box at the end of each day. If you do something interesting (or non-interesting) with the data, let me know!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2018-11-16
WRT the comment 2017-11-17, and exactly one year later, I had the same thing happen whilst running MENACE in a 'Resign' loop for a few hours, unattended. When I returned, the orange overlay had appeared, making the screen quite difficult to read on an iPad.g0mrb
On the JavaScript version, MENACE2 (a second version of MENACE which learns in the same way, to play against the original) keeps setting the 6th move as NaN, meaning it cannot function. Is there a fix for this?
Lambert
what would happen if you loaded the boxes slightly differently. if you started with one bead corresponding to each move in each box. if the bead caused the machine to lose you remove only that bead. if the game draws you leave the bead in play if the bead causes a win you put an extra bead in each of the boxes that led to the win. if the box becomes empty you remove the bead that lead to that result from the box before
Ian
Hi, I was playing with MENACE, and after a while the page redrew with a Dragon Curves design over the top. MENACE was still working alright but it was difficult to see what I was doing due to the overlay. I did a screen capture of it if you want to see it.
Russ
Add a Comment
2016-10-08
During my Electromagnetic Field talk this year, I spoke about @mathslogicbot, my Twitter bot that is working its way through the tautologies in propositional calculus. My talk included my conjecture that the number of tautologies of length \(n\) is an increasing sequence (except when \(n=8\)). After my talk, Henry Segerman suggested that I also look at the number of contradictions of length \(n\) to look for insights.
A contradiction is the opposite of a tautology: it is a formula that is False for every assignment of truth values to the variables. For example, here are a few contradictions:
$$\neg(a\leftrightarrow a)$$
$$\neg(a\rightarrow a)$$
$$(\neg a\wedge a)$$
$$(\neg a\leftrightarrow a)$$
The first eleven terms of the sequence whose \(n\)th term is the number of contradictions of length \(n\) are:
$$0, 0, 0, 0, 0, 6, 2, 20, 6, 127, 154$$
This sequence is A277275 on OEIS. A list of contractions can be found here.
For the same reasons as the sequence of tautologies, I would expect this sequence to be increasing. Surprisingly, it is not increasing for small values of \(n\), but I again conjecture that it is increasing after a certain point.
Properties of the sequences
There are some properties of the two sequences that we can show. Let \(a(n)\) be the number of tautolgies of length \(n\) and let \(b(n)\) be the number of contradictions of length \(n\).
First, the number of tautologies and contradictions, \(a(n)+b(n)\), (A277276) is an increasing sequence. This is due to the facts that \(a(n+1)\geq b(n)\) and \(b(n+1)\geq a(n)\), as every tautology of length \(n\) becomes a contraction of length \(n+1\) by appending a \(\neg\) to be start and vice versa.
This implies that for each \(n\), at most one of \(a\) and \(b\) can be decreasing at \(n\), as if both were decreasing, then \(a+b\) would be decreasing. Sadly, this doesn't seem to give us a way to prove the conjectures, but it is a small amount of progress towards them.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-06-05
The Game of Life is a cellular automaton invented by John Conway in 1970,
and popularised by Martin Gardner.
In Life, cells on a square grid are either alive or dead. It begins
at generation 0 with some cells alive and some dead. The cells' aliveness in
the following generations are defined by the following rules:
- Any live cell with four or more live neighbours dies of overcrowding.
- Any live cell with one or fewer live neighbours dies of loneliness.
- Any dead cell with exactly three live neighbours comes to life.
Starting positions can be found which lead to all kinds of behaviour:
from making gliders
to generating prime numbers.
The following starting position is one of my favourites:
![](javascript:showlimage("mslife1.png"))
It looks boring enough, but in the next generation, it will look like this:
![](javascript:showlimage("mslife2.png"))
If you want to confirm that I'm not lying, I recommend the free Game of Life Software Golly.
Going backwards
You may be wondering how I designed the starting pattern above. A first, it looks like a difficult task: each cell can be dead or alive,
so I need to check every possible combination until I find one. The number of combinations will be \(2^\text{number of cells}\). This will
be a very large number.
There are simplifications that can be made, however. Each of the letters above (ignoring the gs) is in a 3×3 block, surrounded
by dead cells. Only the cells in the 5×5 block around this can affect the letter. These 5×5 blocks do no overlap, so can be
calculated seperately. I doesn't take too long to try all the possibilities for these 5×5 blocks. The gs were then made by starting with an o and trying adding cells below.
Can I make my name?
Yes, you can make your name.
I continued the search and found a 5×5 block for each letter. Simply Enter your name in the box below and
these will be combined to make a pattern leading to your name!
×12 ×13 ×11 ×12 ×12(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2015-08-29
A few weeks ago, I made OEISbot, a Reddit bot which posts information whenever an OEIS sequence is mentioned.
This post explains how OEISbot works. The full code can be found on GitHub.
Getting started
OEISbot is made in Python using PRAW (Python Reddit Api Wrapper). PRAW can be installed with:
bash
pip install prawBefore making a bot, you will need to make a Reddit account for your bot, create a Reddit app and obtain API keys. This python script can be used to obtain the necessary keys.
Once you have your API keys saved in your praw.ini file, you are ready to make a bot.
Writing the bot
First, the necessary imports are made, and test mode is activated if the script is run with test as an argument. We also define an exception that will be used later to kill the script once it makes a comment.
python
import prawimport re
import urllib
import json
from praw.objects import MoreComments
import sys
test = False
if len(sys.argv) > 1 and sys.argv[1] == "test":
test = True
print("TEST MODE")
class FoundOne(BaseException):
pass
To prevent OEISbot from posting multiple links to the same sequence in a thread, lists of sequences linked to in each thread can be loaded and saved using the following functions.
python
def save_list(seen, _id):print(seen)
with open("/home/pi/OEISbot/seen/"+_id, "w") as f:
return json.dump(seen, f)
def open_list(_id):
try:
with open("/home/pi/OEISbot/seen/" + _id) as f:
return json.load(f)
except:
return []
The following function will search a post for a mention of an OEIS sequence number.
python
def look_for_A(id_, text, url, comment):seen = open_list(id_)
re_s = re.findall("A([0-9]{6})", text)
re_s += re.findall("oeis\.org/A([0-9]{6})", url)
if test:
print(re_s)
post_me = []
for seq_n in re_s:
if seq_n not in seen:
post_me.append(markup(seq_n))
seen.append(seq_n)
if len(post_me) > 0:
post_me.append(me())
comment(joiner().join(post_me))
save_list(seen, id_)
raise FoundOne
The following function will search a post for a comma-separated list of numbers, then search for it on the OEIS. If there are 14 sequences or less found, it will reply. If it finds a list with no matches on the OEIS, it will message /u/PeteOK, as he likes hearing about possibly new sequences.
python
def look_for_ls(id_, text, comment, link, message):seen = open_list(id_)
if test:
print(text)
re_s = re.findall("([0-9]+\, *(?:[0-9]+\, *)+[0-9]+)", text)
if len(re_s) > 0:
for terms in ["".join(i.split(" ")) for i in re_s]:
if test:
print(terms)
if terms not in seen:
seen.append(terms)
first10, total = load_search(terms)
if test:
print(first10)
if len(first10)>0 and total <= 14:
if total == 1:
intro = "Your sequence (" + terms \
+ ") looks like the following OEIS sequence."
else:
intro = "Your sequence (" + terms + \
+ ") may be one of the following OEIS sequences."
if total > 4:
intro += " Or, it may be one of the " + str(total-4) \
+ " other sequences listed [here]" \
"(http://oeis.org/search?q=" + terms + ")."
post_me = [intro]
if test:
print(first10)
for seq_n in first10[:4]:
post_me.append(markup(seq_n))
seen.append(seq_n)
post_me.append(me())
comment(joiner().join(post_me))
save_list(seen, id_)
raise FoundOne
elif len(first10) == 0:
post_me = ["I couldn't find your sequence (" + terms \
+ ") in the [OEIS](http://oeis.org). "
"You should add it!"]
message("PeteOK",
"Sequence not in OEIS",
"Hi Peter, I've just found a new sequence (" \
+ terms + ") in [this thread](link). " \
"Please shout at /u/mscroggs to turn the " \
"feature off if its spamming you!")
post_me.append(me())
comment(joiner().join(post_me))
save_list(seen, id_)
raise FoundOne
def load_search(terms):
src = urllib.urlopen("http://oeis.org/search?fmt=data&q="+terms).read()
ls = re.findall("href=(?:'|\")/A([0-9]{6})(?:'|\")", src)
try:
tot = int(re.findall("of ([0-9]+) results found", src)[0])
except:
tot = 0
return ls, tot
The markup function loads the necessary information from OEIS and formats it. Each comment will end with the output of the me function. The ouput of joiner will be used between sequences which are mentioned.
python
def markup(seq_n):pattern = re.compile("%N (.*?)<", re.DOTALL|re.M)
desc = urllib.urlopen("http://oeis.org/A" + seq_n + "/internal").read()
desc = pattern.findall(desc)[0].strip("\n")
pattern = re.compile("%S (.*?)<", re.DOTALL|re.M)
seq = urllib.urlopen("http://oeis.org/A" + seq_n + "/internal").read()
seq = pattern.findall(seq)[0].strip("\n")
new_com = "[A" + seq_n + "](http://oeis.org/A" + seq_n + "/): "
new_com += desc + "\n\n"
new_com += seq + "..."
return new_com
def me():
return "I am OEISbot. I was programmed by /u/mscroggs. " \
"[How I work](http://mscroggs.co.uk/blog/20). " \
"You can test me and suggest new features at /r/TestingOEISbot/."
def joiner():
return "\n\n- - - -\n\n"
Next, OEISbot logs into Reddit.
python
r = praw.Reddit("OEIS link and description poster by /u/mscroggs.")access_i = r.refresh_access_information(refresh_token=r.refresh_token)
r.set_access_credentials(**access_i)
auth = r.get_me()
The subs which OEISbot will search through are listed. I have used all the math(s) subs which I know about, as these will be the ones mentioning sequences.
python
subs = ["TestingOEISbot","math","mathpuzzles","casualmath","theydidthemath","learnmath","mathbooks","cheatatmathhomework","matheducation",
"puremathematics","mathpics","mathriddles","askmath",
"recreationalmath","OEIS","mathclubs","maths"]
if test:
subs = ["TestingOEISbot"]
For each sub OEISbot is monitoring, the hottest 10 posts are searched through for mentions of sequences. If a mention is found, a reply is generated and posted, then the FoundOne exception will be raised to end the code.
python
try:for sub in subs:
print(sub)
subreddit = r.get_subreddit(sub)
for submission in subreddit.get_hot(limit = 10):
if test:
print(submission.title)
look_for_A(submission.id,
submission.title + "|" + submission.selftext,
submission.url,
submission.add_comment)
look_for_ls(submission.id,
submission.title + "|" + submission.selftext,
submission.add_comment,
submission.url,
r.send_message)
flat_comments = praw.helpers.flatten_tree(submission.comments)
for comment in flat_comments:
if ( not isinstance(comment, MoreComments)
and comment.author is not None
and comment.author.name != "OEISbot" ):
look_for_A(submission.id,
re.sub("\[[^\]]*\]\([^\)*]\)","",comment.body),
comment.body,
comment.reply)
look_for_ls(submission.id,
re.sub("\[[^\]]*\]\([^\)*]\)","",comment.body),
comment.reply,
submission.url,
r.send_message)
except FoundOne:
pass
Running the code
I put this script on a Raspberry Pi which runs it every 10 minutes (to prevent OEISbot from getting refusals for posting too often). This is achieved with a cron job.
bash
*/10 * * * * python /path/to/bot.pyMaking your own bot
The full OEISbot code is available on GitHub. Feel free to use it as a starting point to make your own bot! If your bot is successful, let me know about it in the comments below or on Twitter.
Edit: Updated to describe the latest version of OEISbot.
×3 ×4 ×3 ×3 ×3(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2015-08-27
In 1961, Donald Michie built MENACE (Machine Educable Noughts And Crosses Engine), a machine capable of learning to be a better player of Noughts and Crosses (or Tic-Tac-Toe if you're American). As computers were less widely available at the time, MENACE was built from from 304 matchboxes.
![](javascript:showlimage("menace.jpg"))
Taken from Trial and error by Donald Michie [2]
The original MENACE.
To save you from the long task of building a copy of MENACE, I have written a JavaScript version of MENACE, which you can play against here.
How to play against MENACE
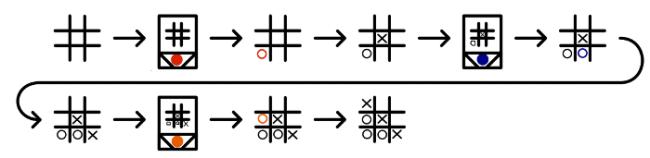
To reduce the number of matchboxes required to build it, MENACE always plays first. Each possible game position which MENACE could face is drawn on a matchbox. A range of coloured beads are placed in each box. Each colour corresponds to a possible move which MENACE could make from that position.
To make a move using MENACE, the box with the current board position must be found. The operator then shakes the box and opens it. MENACE plays in the position corresponding to the colour of the bead at the front of the box.
For example, in this game, the first matchbox is opened to reveal a red bead at its front. This means that MENACE (O) plays in the corner. The human player (X) then plays in the centre. To make its next move, MENACE's operator finds the matchbox with the current position on, then opens it. This time it gives a blue bead which means MENACE plays in the bottom middle.
![](javascript:showlimage("menace-example.png"))
The human player then plays bottom right. Again MENACE's operator finds the box for the current position, it gives an orange bead and MENACE plays in the left middle. Finally the human player wins by playing top right.
MENACE has been beaten, but all is not lost. MENACE can now learn from its mistakes to stop the happening again.
How MENACE learns
MENACE lost the game above, so the beads that were chosen are removed from the boxes. This means that MENACE will be less likely to pick the same colours again and has learned. If MENACE had won, three beads of the chosen colour would have been added to each box, encouraging MENACE to do the same again. If a game is a draw, one bead is added to each box.
Initially, MENACE begins with four beads of each colour in the first move box, three in the third move boxes, two in the fifth move boxes and one in the final move boxes. Removing one bead from each box on losing means that later moves are more heavily discouraged. This helps MENACE learn more quickly, as the later moves are more likely to have led to the loss.
After a few games have been played, it is possible that some boxes may end up empty. If one of these boxes is to be used, then MENACE resigns. When playing against skilled players, it is possible that the first move box runs out of beads. In this case, MENACE should be reset with more beads in the earlier boxes to give it more time to learn before it starts resigning.
How MENACE performs
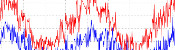
In Donald Michie's original tournament against MENACE, which lasted 220 games and 16 hours, MENACE drew consistently after 20 games.
![](javascript:showlimage("menace-graph.jpg"))
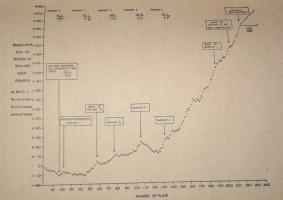
Taken from Trial and error by Donald Michie [2]
![](javascript:showlimage("michie-copy-annot.png"))
Graph showing MENACE's performance in the original tournament. Edit: Added the redrawn graph on the left.
After a while, Michie tried playing some more unusual games. For a while he was able to defeat MENACE, but MENACE quickly learnt to stop losing. You can read more about the original MENACE in A matchbox game learning-machine by Martin Gardner [1] and Trial and error by Donald Michie [2].
You may like to experiment with different tactics against MENACE yourself.
Play against MENACE
I have written a JavaScript implemenation of MENACE for you to play against. The source code for this implementation is available on GitHub.
When playing this version of MENACE, the contents of the matchboxes are shown on the right hand side of the page. The numbers shown on the boxes show how many beads corresponding to that move remain in the box. The red numbers show which beads have been picked in the current game.
The initial numbers of beads in the boxes and the incentives can be adjusted by clicking Adjust MENACE's settings above the matchboxes. My version of MENACE starts with more beads in each box than the original MENACE to prevent the early boxes from running out of beads, causing MENACE to resign.
Additionally, next to the board, you can set MENACE to play against random, or a player 2 version of MENACE.
Edit: After hearing me do a lightning talk about MENACE at CCC, Oliver Child built a copy of MENACE. Here are some pictures he sent me:
![](javascript:showlimage("menace1s.jpg"))
![](javascript:showlimage("menace3s.jpg"))
![](javascript:showlimage("menace4s.jpg"))
Edit: Oliver has written about MENACE and the version he built in issue 03 of Chalkdust Magazine.
Edit: Inspired by Oliver, I have built my own MENACE. I took it to the MathsJam Conference 2016. It looks like this:
![](javascript:showlimage("my_menace.jpg"))
References
[2] Trial and error by Donald Michie. Penguin Science Survey, 1961.
×30 ×28 ×26 ×22 ×24(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
This is very neat. I wonder how long it would take to use that many matches to get all those match boxes.×14 ×13 ×6 ×3 ×3
Duke Nukem
×14 ×13 ×6 ×3 ×3 "When playing against skilled players, it is possible that the first move box runs out of beads. In this case, MENACE should be reset with more beads in the earlier boxes to give it more time to learn before it starts resigning."
If someone were doing this, you could do this automatically to avoid the perception or temptation of the operator to help it along. Instead of "oh, it's dead, let's repopulate the boxes", you could just make it part of the inter-game cleanup, like a garbage collection routine. After all the bead deleting/adding whatever, but before the next game starts, look at all the boxes, make sure that each box contains at least one of each color. Now this weakens the learning algorithm moderately, but it guarantees that it will never get stuck.×3 ×7 ×3 ×4 ×4
If someone were doing this, you could do this automatically to avoid the perception or temptation of the operator to help it along. Instead of "oh, it's dead, let's repopulate the boxes", you could just make it part of the inter-game cleanup, like a garbage collection routine. After all the bead deleting/adding whatever, but before the next game starts, look at all the boxes, make sure that each box contains at least one of each color. Now this weakens the learning algorithm moderately, but it guarantees that it will never get stuck.
(anonymous)
×3 ×7 ×3 ×4 ×4 @Matthew: Thank you for such a quick response. Just to let you know that that link did not work after .../tree/master/output, but I managed to search around for the right files :). In these files MENACE plays the Nought right? and the user plays the Cross?
×2 ×2 ×2 ×2 ×2
(anonymous)
×2 ×2 ×2 ×2 ×2 @Finlay: You can find them at https://github.com/mscroggs/MENACE-pdf.... The files boxes0.pdf to boxes3.pdf are the boxes for a MENACE that plays first.×2 ×4 ×3 ×2 ×3
Matthew
×2 ×4 ×3 ×2 ×3 Add a Comment