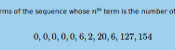Blog
2015-03-15
A few months ago, I set
@mathslogicbot (and @logicbot@mathstodon.xyz and @logicbot.bsky.social) going on the
long task of tweeting all the tautologies (containing 140 characters or less)
in propositional calculus with the symbols \(\neg\) (not), \(\rightarrow\)
(implies), \(\leftrightarrow\) (if and only if), \(\wedge\) (and) and \(\vee\)
(or). My first post on logic bot contains a full
explanation of propositional calculus, formulae and tautologies.
An alternative method
Since writing the original post, I have written an alternative script to
generate all the tautologies.
In this new method, I run through all possible strings of length 1 made
with character in the logical language, then strings of length 2, 3 and so on.
The script then checks if they are valid formulae and, if so, if they are
tautologies.
In the new script, only formulae where the first appearances of variables
are in alphabetical order are considered. This means that duplicate tautologies
are removed. For example, \((b\rightarrow(b\wedge a))\) will now be counted as
it is the same as \((a\rightarrow(a\wedge b))\).
You can view or download this alternative code on
github.
All the terms of the sequence that I have calculated so far can be viewed
here and the tautologies for these terms are
here.
Sequence
One advantage of this method is that it generates the tautologies sorted by
the number of symbols they contain, meaning we can generate the sequence whose
\(n\)th term is the number of tautologies of length \(n\).
The first ten terms of this sequence are
$$0, 0, 0, 0, 2, 2, 12, 6, 57, 88$$
as there are no tautologies of length less than 5; and, for example two
tautologies of length 6 (\((\neg a\vee a)\) and \((a\vee \neg a)\)).
This sequence is listed as
A256120 on OEIS.
Properties
There are a few properties of this sequence that can easily be shown.
Throughout this section I will use \(a_n\) to represent the \(n\)th
term of the sequence.
Firstly, \(a_{n+2}\geq a_n\). This can be explained as follows: let \(A\)
be a tautology of length \(n\). \(\neg\neg A\) will be of length \(n+2\) and
is logically equivalent to \(A\).
Another property is \(a_{n+4}\geq 2a_n\): given a tautology \(A\) of length
\(n\), both \((a\vee A)\) and \((A\vee a)\) will be tautologies of length
\(n+4\). Similar properties could be shown for \(\rightarrow\),
\(\leftrightarrow\) and \(\wedge\).
Given properties like this, one might predict that the sequence will be
increasing (\(a_{n+1}\geq a_n\)). However this is not true as \(a_7\) is 12
and \(a_8\) is only 6. It would be interesting to know at how many points in
the sequence there is a term that is less than the previous one. Given the
properties above it is reasonable to conjecture that this is the only one.
Edit: The sequence has been published on OEIS!
Edit: Added Mastodon and Bluesky links
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2023-02-09) ⭐
Great project! Would be interesting to have a version of this for the sheffer stroke.om
Add a Comment
2014-11-26
Last week, @mathslogicbot (also now on Mastodon (@logicbot@mathstodon.xyz) and Bluesky (@logicbot.bsky.social)) started the long task of tweeting every tautology in propositional calculus. This post explains what this means and how I did it.
What is propositional calculus?
Propositional calculus is a form of mathematical logic, in which the formulae (the logical 'sentences') are made up of the following symbols:
- Variables (a to z and \(\alpha\) to \(\lambda\)) (Variables are usually written as \(p_1\), \(p_2\), etc. but as Twitter cannot display subscripts, I chose to use letters instead.)
- Not (\(\neg\))
- Implies (\(\rightarrow\))
- If and only if (\(\leftrightarrow\))
- And (\(\wedge\))
- Or (\(\vee\))
- Brackets (\(()\))
Formulae
Formulae are defined recursively using the following rules:
- Every variable is a formula.
- If \(A\) is a formula, then \(\neg A\) is a formula.
- If \(A\) and \(B\) are formulae then \((A\rightarrow B)\), \((A\leftrightarrow B)\), \((A\wedge B)\) and \((A\vee B)\) are all formulae.
For example, \((a\vee b)\), \(\neg f\) and \(((a\vee b)\rightarrow\neg f)\) are formulae.
Each of the variables is assigned a value of either "true" or "false", which leads to each formula being either true or false:
- \(\neg a\) is true if \(a\) is false (and false otherwise).
- \((a\wedge b)\) is true if \(a\) and \(b\) are both true (and false otherwise).
- \((a\vee b)\) is true if \(a\) or \(b\) is true (or both are true) (and false otherwise).
- \((a\leftrightarrow b)\) is true if \(a\) and \(b\) are either both true or both false (and false otherwise).
- (\(a \rightarrow\ b)\) is true if \(a\) and \(b\) are both true or \(a\) is false (and false otherwise).
Tautologies
A tautology is a formula that is true for any assigment of truth values to the variables. For example:
\((a\vee \neg a)\) is a tautology because: if \(a\) is true then \(a\) or \(\neg a\) is true; and if \(a\) is false, then \(\neg a\) is true, so \(a\) or \(\neg a\) is true.
\((a\leftrightarrow a)\) is a tautology because: if \(a\) is true then \(a\) and \(a\) are both true; and if \(a\) is false then \(a\) and \(a\) are both false.
\((a\wedge b)\) is not a tautology because if \(a\) is true and \(b\) is false, then it is false.
The following are a few more tautologies. Can you explain why they are always true?
- \((a\leftrightarrow a)\)
- \(((a\vee\neg a)\vee a)\)
- \(\neg(a\wedge\neg a)\)
- \((a\vee(a\rightarrow b))\)
Python
If you want to play with the Logic Bot code, you can download it here.
In order to find all tautologies less than 140 characters long, one method is to first generate all formulae less than 140 characters then check to see if they are tautologies. (This is almost certainly not the fastest way to do this, but as long as it generates tautolgies faster than I want to tweet them, it doesn't matter how fast it runs.) I am doing this on a Raspberry Pi using Python in the following way.
All formulae
The following code is writing all the formulae that are less than 140 characters to a file called formulae.
python
from os.path import joinpath = "/home/pi/logic"
First import any modules needed and set the path where the file will be saved.
python
def candidate(formula):global formulae
if len(formula) <= 140 and formula not in formulae:
formulae.append(formula)
print formula
f = open(join(path,"formulae"),"a")
f.write(formula + "\n")
f.close()
This function checks that a formula is not already in my list of formulae and shorter than 140 characters, then adds it to the list and writes it into the file.
python
variables = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j","k", "l", "m", "n", "o", "p", "q", "r", "s", "t",
"u", "v", "w", "x", "y", "z", "@", "#", "2", "3",
"4", "5", "6", "7", "8", "9"]
This line says which characters are going to be used as variables. It is impossible to write a formula in less that 140 characters with more than 36 different variables so these will be sufficient. I haven't used 0 and 1 as these are used to represent false and true later.
python
f = open(join(path,"formulae"))formulae = f.readlines()
for i in range(0,len(formulae)):
formulae[i] = formulae[i].strip("\n")
f.close()
These lines load the formulae already found from the file. This is needed if I have to stop the code then want to continue.
python
oldlen = 0newlen = 26
while oldlen != newlen:
for f in formulae + variables:
candidate("-" + f)
for f in formulae + variables:
for g in formulae:
for star in ["I", "F", "N", "U"]:
candidate("(" + f + star + g + ")")
oldlen = newlen
newlen = len(formulae)
The code inside the while loop goes through every formula already found and puts "-" in front of it, then takes every pair of formulae already found and puts "I", "F", "N" or "U" between them. These characters are used instead of the logical symbols as using the unicode characters leads to numerous python errors. The candidate function as defined above then adds them to the list (if they are suitable). This continues until the loop does not make the list of formulae longer as this will occur when all formulae are found.
python
f = open(join(path,"formulae"),"a")f.write("#FINISHED#")
f.close()
Once the loop has finished this will add the string "#FINISHED#" to the file. This will tell the truth-checking code when the it has checked all the formulae (opposed to having checked all those generated so far).
Tautologies
Now that the above code is finding all formulae, I need to test which of these are tautologies. This can be done by checking whether every assignment of truth values to the variables will lead to the statement being true.
python
from os.path import joinpath = "/home/pi/logic"
First import any modules needed and set the path where the file will be saved.
python
def next(ar,i=0):global cont
if i < len(ar):
if ar[i] == "0":
ar[i] = "1"
else:
ar[i] = "0"
ar = next(ar, i + 1)
else:
cont = False
return ar
Given an assignment of truth values, this function will return the next assignment, setting cont to False if all the assignments have been tried.
python
def solve(lo):lo = lo.replace("-0", "1")
lo = lo.replace("-1", "0")
lo = lo.replace("(0I0)", "1")
lo = lo.replace("(0I1)", "1")
lo = lo.replace("(1I0)", "0")
lo = lo.replace("(1I1)", "1")
lo = lo.replace("(0F0)", "1")
lo = lo.replace("(0F1)", "0")
lo = lo.replace("(1F0)", "0")
lo = lo.replace("(1F1)", "1")
lo = lo.replace("(0N0)", "0")
lo = lo.replace("(0N1)", "0")
lo = lo.replace("(1N0)", "0")
lo = lo.replace("(1N1)", "1")
lo = lo.replace("(0U0)", "0")
lo = lo.replace("(0U1)", "1")
lo = lo.replace("(1U0)", "1")
lo = lo.replace("(1U1)", "1")
return lo
This function will replace all instances of "NOT TRUE" with "FALSE" and so on. It will be called repeatedly until a formula is reduced to true or false.
python
f = open(join(path,"formulae"))formulae = f.readlines()
f.close()
f = open(join(path,"donet"))
i = int(f.read())
f.close()
variables = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j",
"k", "l", "m", "n", "o", "p", "q", "r", "s", "t",
"u", "v", "w", "x", "y", "z", "@", "#", "2", "3",
"4", "5", "6", "7", "8", "9"]
These lines read the formulae from the file they are saved in and load how many have been checked if this script has been restarted. The the variables are set.
python
while formulae[-1] != "#FINISHED#" or i < len(formulae) - 1:if i < len(formulae):
formula = formulae[i].strip("\n")
These lines will loop through all formulae until "#FINISHED#" is reached.
python
insofar = TrueinA = []
fail = False
for a in variables:
if a not in formula:
insofar = False
elif not insofar:
fail = True
break
else:
inA.append(a)
Here, the code checks that if a variable is in the formula, then all the previous variables are in the formula. This will prevent the Twitter bot from repeating many tautologies that are the same except for the variable a being replaced by b (although there will still be some repeats like this. Can you work out what these will be?).
python
if not fail:valA = ["0"]*len(inA)
cont = True
taut = True
while cont and taut:
feval = formula
for j in range(0,len(inA)):
feval = feval.replace(inA[j],valA[j])
while feval not in ["0", "1"]:
feval = solve(feval)
if feval != "1":
taut = False
valA = next(valA)
if taut:
f = open(join(path,"true"),"a")
f.write(str(formula) + "\n")
f.close()
i += 1
f = open(join(path,"donet"),"w")
f.write(str(i))
f.close()
Now, the formula is tested to see if it is true for every assignment of truth values. If it is, it is added to the file containing tautologies. Then the number of formulae that have been checked is written to a file (in case the script is stopped then resumed).
python
else:f = open(join(path,"formulae"))
formulae = f.readlines()
f.close()
If the end of the formulae file is reached, then the file is re-loaded to include all the formulae found while this code was running.
Tweeting
Finally, I wrote a code that tweets the next item in the file full of tautologies every three hours (after replacing the characters with the correct unicode characters).
How long will it take?
Now that the bot is running, it is natural to ask how long it will take to tweet all the tautologies.
While it is possible to calculate the number of formulae with 140 characters or less, there is no way to predict how many of these will be tautologies without checking. However, the bot currently has over 13 years of tweets lines up. And all the tautologies so far are under 30 characters so there are a lot more to come...
Edit: Updated time left to tweet.
Edit: Added Mastodon and Bluesky links
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
In part two you say a_{n+4} >= 2*a_n, and you have 13 years worth of tweets of length (say) 15-30. so there are 26 years worth length 19-34 characters, 13*2^n years worth of tweets of length between (15 + 4n) and (30 + 4n). In particular, setting n = 27, we have 13*2^{27} = 1744830464 years worth of tweets of length 123-138. I hope you have nice sturdy hardware!
Christian
Add a Comment
2013-07-11
On 19 June, the USB temperature sensor I ordered from Amazon arrived. This sensor is now hooked up to my Raspberry Pi, which is taking the temperature every 10 minutes, drawing graphs, then uploading them here. Here is a brief outline of how I set this up:
Reading the temperature
I found this code and adapted it to write the date, time and temperature to a text file. I then set cron to run this every 10 minutes. It writes the data to a text file (/var/www/temperature2) in this format:
2013 06 20 03 50,16.445019
2013 06 20 04 00,16.187843
2013 06 20 04 10,16.187843
2013 06 20 04 20,16.187843
2013 06 20 04 00,16.187843
2013 06 20 04 10,16.187843
2013 06 20 04 20,16.187843
Plotting the graphs
I found a guide somewhere on the internet about how to draw graphs with Python using Pylab/Matplotlib. If you have any idea where this could be, comment below and I'll put a link here.
In the end my code looked like this:
python
import timeimport matplotlib as mpl
mpl.use("Agg")
import matplotlib.pylab as plt
import matplotlib.dates as mdates
ts = time.time()
import datetime
now = datetime.datetime.fromtimestamp(ts)
st = mdates.date2num(datetime.datetime(int(float(now.strftime("%Y"))),
int(float(now.strftime("%m"))),
int(float(now.strftime("%d"))),
0, 0, 0))
weekst = st - int(float(datetime.datetime.fromtimestamp(ts).strftime("%w")))
f = file("/var/www/temperature2","r")
t = []
s = []
tt = []
ss = []
u = []
v = []
g = []
h = []
i = []
weekt = []
weektt = []
weeks = []
weekss = []
mini = 1000
maxi = 0
cur = -1
datC = 0
for line in f:
fL = line.split(",")
fL[0] = fL[0].split(" ")
if cur == -1:
cur = mdates.date2num(datetime.datetime(int(float(fL[0][0])),
int(float(fL[0][1])),
int(float(fL[0][2])),
0,0,0))
datC = mdates.date2num(datetime.datetime(int(float(fL[0][0])),
int(float(fL[0][1])),
int(float(fL[0][2])),
int(float(fL[0][3])),
int(float(fL[0][4])),
0))
u.append(datC)
v.append(fL[1])
if datC >= st and datC <= st + 1:
t.append(datC)
s.append(fL[1])
if datC >= st - 1 and datC <= st:
tt.append(datC + 1)
ss.append(fL[1])
if datC >= weekst and datC <= weekst + 7:
weekt.append(datC)
weeks.append(fL[1])
if datC >= weekst - 7 and datC <= weekst:
weektt.append(datC + 7)
weekss.append(fL[1])
if datC > cur + 1:
g.append(cur)
h.append(mini)
i.append(maxi)
mini = 1000
maxi = 0
cur = mdates.date2num(datetime.datetime(int(float(fL[0][0])),
int(float(fL[0][1])),
int(float(fL[0][2])),
0,0,0))
mini = min(float(fL[1]),mini)
maxi = max(float(fL[1]),maxi)
g.append(cur)
h.append(mini)
i.append(maxi)
plt.plot_date(x=t,y=s,fmt="r-")
plt.plot_date(x=tt,y=ss,fmt="g-")
plt.xlabel("Time")
plt.ylabel("Temperature (#^\circ#C)")
plt.title("Daily")
plt.legend(["today","yesterday"], loc="upper left",prop={"size":8})
plt.grid(True)
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter("%H:%M"))
plt.gcf().subplots_adjust(bottom=0.15,right=0.99)
labels = plt.gca().get_xticklabels()
plt.setp(labels,rotation=90,fontsize=10)
plt.xlim(st,st + 1)
plt.savefig("/var/www/tempr/tg1p.png")
plt.clf()
plt.plot_date(x=weekt,y=weeks,fmt="r-")
plt.plot_date(x=weektt,y=weekss,fmt="g-")
plt.xlabel("Day")
plt.ylabel("Temperature (#^\circ#C)")
plt.title("Weekly")
plt.legend(["this week","last week"], loc="upper left",prop={"size":8})
plt.grid(True)
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter(" %A"))
plt.gcf().subplots_adjust(bottom=0.15,right=0.99)
labels = plt.gca().get_xticklabels()
plt.setp(labels,rotation=0,fontsize=10)
plt.xlim(weekst,weekst + 7)
plt.savefig("/var/www/tempr/tg2p.png")
plt.clf()
plt.plot_date(x=u,y=v,fmt="r-")
plt.xlabel("Date & Time")
plt.ylabel("Temperature (#^\circ#C)")
plt.title("Forever")
plt.grid(True)
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter("%d/%m/%y %H:%M"))
plt.gcf().subplots_adjust(bottom=0.25,right=0.99)
labels = plt.gca().get_xticklabels()
plt.setp(labels,rotation=90,fontsize=8)
plt.savefig("/var/www/tempr/tg4p.png")
plt.clf()
plt.plot_date(x=g,y=h,fmt="b-")
plt.plot_date(x=g,y=i,fmt="r-")
plt.xlabel("Date")
plt.ylabel("Temperature (#^\circ#C)")
plt.title("Forever")
plt.legend(["minimum","maximum"], loc="upper left",prop={"size":8})
plt.grid(True)
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter("%d %b"))
plt.gcf().subplots_adjust(bottom=0.15,right=0.99)
labels = plt.gca().get_xticklabels()
plt.setp(labels,rotation=90,fontsize=8)
plt.savefig("/var/www/tempr/tg3p.png")
If there's anything in there you don't understand, comment below and I'll try to fill in the gaps.
Uploading the graphs
Finally, I upload the graphs to mscroggs.co.uk/weather.
To do this, I set up pre-shared keys on the Raspberry Pi and this server and added
the following as a cron job:
bash
0 * * * * scp /var/www/tempr/tg*p.png username@mscroggs.co.uk:/path/to/folder
I hope this was vaguely interesting/useful. I'll try to add more details and updates over time. If you are building something similar, please let me know in the comments; I'd love to see what everyone else is up to.
Edit: Updated to reflect graphs now appearing on mscroggs.co.uk not catsindrag.co.uk.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment