Blog
2024-01-07
Welcome to 2024 everyone! Now that the Advent calendar has disappeared, it's time to reveal the answers and announce the winners.
But first, some good news: with your help, the machine was fixed in time for Santa to deliver presents and Christmas was saved!







Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar and a couple of other interesting bits and pieces.
Highlights
My first highlight is the puzzle from 4 December. I like this puzzle, because at first it looks really difficult, and the size of the factorial involved is impossibly large,
but the way of solving it that I used essentially just ignores the factorial leading to a much easier question.
4 December
If \(n\) is 1, 2, 4, or 6 then \((n!-3)/(n-3)\) is an integer. The largest of these numbers is 6.
What is the largest possible value of \(n\) for which \((n!-123)/(n-123)\) is an integer?
My next pair of highlights are the puzzles from 6 and 7 December. I always enjoy a surprise appearance of the Fibonacci sequence, and a double enjoyed a
double appearance in two contexts that at first look completely different.
6 December
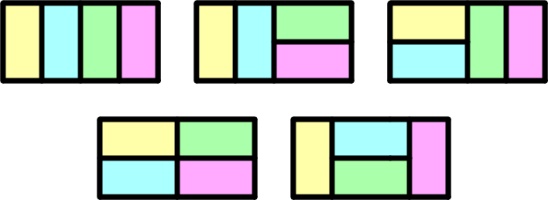
There are 5 ways to tile a 4×2 rectangle with 2×1 pieces:
How many ways are there to tile a 12×2 rectangle with 2×1 pieces?
7 December
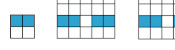
There are 8 sets (including the empty set) that contain numbers from 1 to 4 that don't include any consecutive integers:
How many sets (including the empty set) are there that contain numbers from 1 to 14 that don't include any consecutive integers?
My next highlight is the puzzle from 13 December. I love a good crossnumber, and had a lot of fun making this small one up. (If you enjoyed this one, you should check out the
crossnumbers I write for Chalkdust.)
13 December
Today's number is given in this crossnumber. No number in the completed grid starts with 0.
|
|
| |||||||||||||||||||||||||||||||||
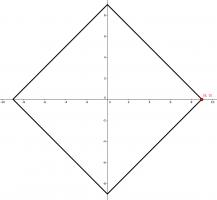
My final highlight is the puzzle from 22 December. I enjoy that you can use one of the circle theorems to solve this, despite there being no circles directly involved in the question.
22 December
There are 4 ways to pick three vertices of a regular quadrilateral so that they form a right-angled triangle:
In another regular polygon with \(n\) sides, there are 14620 ways to pick three vertices so that they form a right-angled triangle. What is \(n\)?
Hardest and easiest puzzles
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
It looks like the hardest puzzles were on
23 and
12 December;
and the easiest puzzles were on
1,
3,
5, and
11 December.
Fixing the machine
To finish the Advent calendar, you were tasked with fixing the machine. The answers to all the puzzles were required to
be certain of which combination of parts were needed to fix the machine, but it was possible to reduce the number of options
to a small number and get lucky when trying these options. This graph shows how many people fixed the machine on each day:
| 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Day | |||||||||||||||
The winners
And finally (and maybe most importantly), on to the winners: 180 people managed to fix the machine. That's slightly fewer than last year:
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Year | ||||||||
From the correct answers, the following 10 winners were selected:
- Matt Thomson
- Matthieu
- Steve Paget
- Millie
- Eleanor
- Alex Bolton
- Brennan Dolson
- UsrBinPRL
- Daniel Low
- Erik
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2023 Advent calendar T-shirts. If you didn't win one, but would like one of these, I've made them available to buy at merch.mscroggs.co.uk alongside the T-shirts from previous years.
Additionally, well done to
100118220919, Aaron, Adam NH, Aidan Dodgson, AirWrek, Alan Buck, Alejandro Villarreal, Alek2ander, Alex, Alex Hartz, Allan Taylor, Andrew Roy, Andrew Thomson, Andrew Turner, Andy Ennaco, Ashley Jarvis, Austin Antoniou, Becky Russell, Ben, Ben Boxall, Ben Reiniger, Ben Tozer, Ben Weiss, Bill Russ, Bill Varcho, Blake, Bogdan, Brian Wellington, Carl Westerlund, Carmen, Carnes Family, Cathy Hooper, Chris Eagle, Chris Hellings, Colin Brockley, Connors of York, Corbin Groothuis, Dan Colestock, Dan May, Dan Rubery, Dan Swenson, Dan Whitman, Daphne, David and Ivy Walbert, David Ault, David Berardo, David Fox, David Kendel, David Mitchell, Deborah Tayler, Diane, Donald Anderson, Duncan S, Dylan Madisetti, Ean, Elise Raphael, Emelie, Emily Troyer, Emma, Eric, Eric Kolbusz, Ewan, Frank Kasell, Fred Verheul, Gabriella Pinter, Gareth McCaughan, Gary M, Gary M. Gerken, George Witty, Gert-Jan, Grant Mullins, Gregory Wheeler, Guillermo Heras Prieto, Heerpal Sahota, Helen, Herschel, Iris Lasthofer, Ivan Molotkov, Jack, Jack H, Jacob Y, James Chapman, Jan Z, Jay N, Jean-Sébastien Turcotte, Jen Sparks, Jenny Forsythe, Jessica Marsh, Jim Ashworth, Joe Gage, Johan, Jon Palin, Jonathan Chaffer, Jonathan Thiele, Jorge del Castillo Tierz, K Brooks, Kai, Karen Climis, Kevin Docherty, Kevin Fray, Kirsty Fish, Kristen Koenigs, lacop, Lazar Ilic, Lewis Dyer, Lisa Stambaugh, Lise Andreasen, Lizzie McLean, Louis, Magnus Eklund, Marco van der Park, Mark Fisher, Mark Stambaugh, Martijn O., Martin Harris, Martin Holtham, Mary Cave, Matthew Schulz, Max, Merrilyn, Mihai Zsisku, Mike Hands, Miles Lunger, Mr J Winfield, Nadine Chaurand, Naomi Bowler, Nathan Whiteoak, Nick C, Nick Keith, Niji Ranger, Pamela Docherty, Pierce R, Qaysed, Rashi, Ray Arndorfer, rea, Reuben Cheung, Riccardo Lani, Richard O, Rob Reynolds, Robby Brady, Roger Lipsett, Roni, Rosie Paterson, RunOnFoot, Ruth Franklin, Ryan Wise, Sage Robinson, Sam Dreilinger, Sarah, Scott, Sean Henderson, Seth Cohen, Shivanshi, Shreevatsa, Stephen Cappella, Steve Blay, TAS, Tehnuka, The Johnston Family, Tina, Tony Mann, Trent Marsh, tripleboleo, Valentin VĂLCIU, Vinny R, William Huang, Yasha, and Yuliya Nesterova,
who all also completed the Advent calendar but were too unlucky to win prizes this time or chose to not enter the prize draw.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2024-01-07) ⭐
In your solution for the 12th, I think there's still a little work to do: to check that the answer is the smallest integer that works. For that, because 241 is prime, you only have a handful of values to check.Ben Reiniger
(you've left the "drones" in at the beginning of the Winners section)
Ben Reiniger
On the 6th and 7th, there's also a direct bijection: in the tiling, horizontal tiles must occur in aligned pairs (else they split left/right into odd number of 1x1 blocks). Encode a tiling with the set of horizontal locations of the left ends of the horizontal-tile-pairs.
Ben Reiniger
Add a Comment
2023-12-08
In November, I spent some time (with help from TD) designing this year's Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 10 puzzles. By colouring in the answers to the puzzles on the front of the card in the colours given (each answer appears four time),
you will reveal a Christmas themed picture.
If you're in the UK and want some copies of the card to send to your maths-loving friends, you can order them at mscroggs.co.uk/cards.
If you want to try the card yourself, you can download this printable A4 pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will automatically be found and coloured in...
Green | ||
| 1. | What is the largest value of \(n\) such that \((n!-1)/(n-1)\) is an integer? | Answer |
| 2. | What is the largest value of \(n\) such that \((n!-44)/(n-44)\) is an integer? | Answer |
Red/blue | ||
| 3. | Holly adds up the first 7 even numbers, then adds on half of the next even number. What total does she get? | Answer |
| 4. | Holly adds up the first \(n\) even numbers, then adds on half of the next even number. Her total was 9025. What is \(n\)? | Answer |
Brown | ||
| 5. | What is the area of the quadrilateral with the largest area that will fit inside a circle with area 20π? | Answer |
| 6. | What is the area of the dodecagon with the largest area that will fit inside a circle with area 20π? | Answer |
| 7. | How many 3-digit positive integers are there whose digits are all 1, 2, 3, 4, or 5 with exactly two digits that are ones? | Answer |
| 8. | Eve works out that there are 300 \(n\)-digit positive integers whose digits are all 1, 2, 3, 4, or 5 with exactly \(n-1\) digits that are ones. What is \(n\)? | Answer |
| 9. | What are the last two digits of \(7^3\)? | Answer |
| 10. | What are the last two digits of \(7^{9876543210}\)? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Incorrect answers are treated is correct.
Looking at the JavaScript code, I found that any value that is a key in the array "regions" is treated as correct for all puzzles.
Looking at the JavaScript code, I found that any value that is a key in the array "regions" is treated as correct for all puzzles.
Lars Nordenström
My visual abilities fail me - managed to solve the puzzles but cannot see what the picture shows
Gantonian
@nochum: It can't, so the answer to that one probably isn't 88.
Matthew
how can a dodecagon with an area of 88 fit inside anything with an area of 62.83~?
nochum
Add a Comment
2023-11-22
This year, the front page of mscroggs.co.uk will once again feature an Advent calendar, just like
in each of the last eight years.
Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a logic puzzle:
It's nearly Christmas and something terrible has happened: a machine in Santa's toy factory has malfunctioned, and is unable to finish building all
the presents that Santa needs.
You need to help Santa work out how to fix the broken machine so that he can build the presents and deliver them before Christmas is ruined for everyone.
Inside the broken machine, there were five toy production units (TPUs) installed at sockets labelled A to E. During the malfunction, these TPUs were
so heavily damaged that Santa is unable to identify which TPU they were when trying to fix the machine. The company that supplies TPUs builds 10 different units, numbered from 0 to 9.
You need to work out which of the 10 TPUs needs to be installed in each of the machine's sockets, so that Santa can fix the machine. It may be that two or more of the TPUs are the same.
Behind each day (except Christmas Day), there is a puzzle with a three-digit answer. Each of these answers forms part of a clue about the machine's TPUs.
You must use these clues to work out which TPU to install in each socket.
You can use this page to plug in five TPUs and test the machine. It takes a significant amount of Santa's time to test the machine, so you
can only run a very small number of tests each day.
Ten randomly selected people who solve all the puzzles, fix the machine, and fill in the entry form behind the door on the 25th will win prizes!
The prizes will include an mscroggs.co.uk Advent 2023 T-shirt. If you'd like one of the T-shirts from a previous Advent, they are available to order at merch.mscroggs.co.uk.
The winners will be randomly chosen from all those who submit the entry form before the end of 2023. Each day's puzzle (and the entry form on Christmas Day) will be available from 5:00am GMT. But as the winners will be selected randomly,
there's no need to get up at 5am on Christmas Day to enter!
As you solve the puzzles, your answers will be stored. To share your stored answers between multiple devices, enter your email address below the calendar and you will be emailed a magic link to visit on your other devices.
To win a prize, you must submit your entry before the end of 2023. Only one entry will be accepted per person. If you have any questions, ask them in the comments below,
on Twitter,
or on Mastodon.
So once December is here, get solving! Good luck and have a very merry Christmas!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Thank you Matthew. 23rd was my favourite puzzle as the cuisenaire rods helped me and I worked with my son to get a final answer. Happy New Year.
Jenny
I really like 22, and will be using it with my top set Year 10s when I do circle theorems next term :)
Artie Smith
I love doing your puzzles, your advent ones as well as the Chalkdust Crossnumbers - thank you!
Merrilyn
Add a Comment
2023-01-08
Welcome to 2023 everyone! Now that the Advent calendar has disappeared, it's time to reveal the answers and announce the winners.
But first, some good news: with your help, the drones were all destroyed in time for Santa to deliver presents and Christmas was saved!
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar and a couple of other interesting bits and pieces.
Highlights
My first highlight is the puzzle from 1 December. I like this puzzle, because the lines of symmetry of a rectangle that you might expect—although it's not too hard to
see what the lines of symmetry are, so this makes a nice gentle first puzzle.
1 December
One of the vertices of a rectangle is at the point \((9, 0)\). The \(x\)-axis and \(y\)-axis are both lines of symmetry of the rectangle.
What is the area of the rectangle?
My next hightlight is the puzzle from 11 December. I always enjoy a surprise appearance of the Fibonacci sequence.
11 December
There are five 3-digit numbers whose digits are all either 1 or 2 and who do not contain
two 2s in a row: 111, 112, 121, 211, and 212.
How many 14-digit numbers are there whose digits are all either 1 or 2 and who do not contain
two 2s in a row?
My next highlight is the puzzle from 13 December. I love a good crossnumber, and had a lot of fun making this small one up. (If you enjoyed this one, you should check out the
crossnumbers I write for Chalkdust.)
13 December
Today's number is given in this crossnumber. The across clues are given as normal, but the down clues are given in a random order: you must work out
which clue goes with each down entry and solve the crossnumber to find today's number.
No number in the completed grid starts with 0.
|
|
| |||||||||||||||||||||||||
My final highlight is the puzzle from 24 December. You could solve this by doing a lot of expanding, but there's a neat shortcut that makes it almost trivial to solve.
24 December
The expression \((3x-1)^2\) can be expanded to give \(9x^2-6x+1\). The
sum of the coefficients in this expansion is \(9-6+1=4\).
What is the sum of the coefficients in the expansion of \((3x-1)^7\)?
Hardest and easiest puzzles
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
11,
18 and
19 December;
and the easiest puzzle was on
8 December.
The winners
And finally (and maybe most importantly), on to the winners: 192 people managed to destroy all three drones. That's more people than last year:
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
| Year | |||||||
From the correct answers, the following 10 winners were selected:
- Claire Metcalfe
- Shivanshi
- Gary M
- Katharine Velleman
- James Dolengewicz
- Cathy Hooper
- Alan Buck
- Yurie Ito
- Kai
- Nicholas Jackson
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2022 Advent calendar T-shirts. If you didn't win one, but would like one of these, I've made them available to buy at merch.mscroggs.co.uk alongside the T-shirts from previous years.
Additionally, well done to
Aaron Johnson, Aaron Stiff, Aidan Dodgson, Alejandro Villarreal, Alek2ander, Alex Bolton, Alex Davis, Alex Hartz, Andrew Brady, Andrew Brodie, Andrew Ennaco, Andrew Roy, Andrew Turner, Artie Smith, Ashton Lewis, Austin Antoniou, Becky Russell, Ben Baker, Ben Boxall, Ben Reiniger, Ben Tozer, Ben Weiss, Beth Jensen, Blake, Brennan Dolson, Brian Carnes, Brian Wellington, Carl Westerlund, Carmen, Charleston W, Chris Eagle, Chris Hellings, Colin Beveridge, Colin Brockley, Connie, Corbin Groothuis, CreativeCrocheter, Dan Colestock, Dan DiMillo, Dan May, Dan Swenson, Dan Whitman, Daniel Cuneo, David and Ivy Walbert, David Ault, David Berardo, David Fox, David Kendel, David Mitchell, Deborah Tayler, Deborah Tayler, Derek Perrin, Dominik Niemand, Don Anderson, Dr Lizzie, Duncan Schaafsma, Dylan Richard, Eleanor, Elizabeth Blackwell, Elizabeth Madisetti, Emilie Heidenreich, Emily Troyer, Emma, Eoin Davey, Eric Kolbusz, Eric Scotti, Erik Eklund, Fionn Woodcock, Frances, Frank Kasell, Fred Verheul, Freddie Mao, Félix Breton, Gabriella Pinter, Gary M. Gerken, Gerry, Gert-Jan, Greg W., Gregory Loges, Greta, Han Whiteoak, Hannah Charman, Heerpal Sahota, Helen F, Herschel, Iris, Jack, Jacob, Jacob Loader, James Chapman, James Cunnane, Jarvis9, Jean-Noël Monette, Jean-Sébastien Turcotte, Jen Sparks, Jessica Marsh, Jim Ashworth, Jon Palin, Jonathan Chaffer, Jonathan Thiele, Jorge del Castillo Tierz, Joseph Gage, Joseph Wagner, Joshua Park, Karen Climis, Kevin Docherty, Kirsty Fish, Kristen Koenigs, Kyle Allen, Lazar Ilic, Lewis Dyer, Lise Andreasen, Louis, LycanFayn, Lyra, Magnus Eklund, Marco van der Park, Mark Stambaugh, Martin Harris, Martin Holtham, Mathryn, Matt Thomson, Mels, Merrilyn, Michael DeLyser, Mihai Zsisku, Mike L, Mike R, Millie, Mr J Winfield, Nadine Chaurand, Nancy Walker, Naomi Bowler, Naomi C, Nick Keith, Niji Ranger, Pamela Docherty, Patrick, Philip Corradi, Priyesh, Pup, Qaysed, Qaysed, Rashi, Ray Arndorfer, Reid, Reuben, Riccardo Lani, Rob Dixon, Robert Brady, Roger Lipsett, Roni Malek, Rosie Paterson, Russ Collins, Ruth Franklin, Sage Robinson, Sam Drei, Sarah Brook, Scott, Sean Henderson, Seth Cohen, shadorfff, Simon English, Stephen Cappella, Stephen Jasina, Sumaya Felic, Tamara Brenner, Tarim, The Connors of York, The Steelblade, Tom Fryers, Tony Mann, tripleboleo, Tyler St Clare, UsrBinPRL, Valentin VĂLCIU, Vinayak, Vinny R, vortex, Yasha, Yuliya N., and Zoran Morrissey-Ralevic.
who all also completed the Advent calendar but were too unlucky to win prizes this time or chose to not enter the prize draw.
See you all next December, when the Advent calendar will return.
Edit: Removed myself (and a second copy of myself) from the list of solvers.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
You didn't mention the rate limiting you put in for the bots!
Sorry about that
Sorry about that
(anonymous)
I fought very hard to solve the middle "here are the 6 answers, construct the 6 small problems", but I just couldn't. Hints about that one and the genre in general would be great.
Lise Andreasen
@Valentin V?LCIU: Oops, forgot to remove my testing that everything works from the list of people! (Removing it now)
Matthew
Add a Comment
2022-12-04
In November, I spent some time (with help from TD) designing this year's Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 11 puzzles. By colouring in the answers to the puzzles on the front of the card in black (each answer appears twice), then colouring remaining squares
containing 0s red, and regions containing a star brown,
you will reveal a Christmas themed picture.
If you want to try the card yourself, you can download this printable A4 pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will automatically be found and coloured in black, and appropriate squares and regions will be coloured red and brown...
The puzzles | ||
| 1. | What is the only prime number that is both two more than a prime number and two less than a prime number? | Answer |
| 2. | Holly adds up the first 7 odd numbers. What total does she get? | Answer |
| 3. | Holly next adds up the first \(n\) odd numbers to get a total of 1089. What is \(n\)? | Answer |
| 4. | Ivy starts with 0 then adds or subtracts some multiples of 4 or 7. What is the smallest positive integer that she could have ended with? | Answer |
| 5. | Ivy again starts with 0, but this time she adds or subtracts some multiples of 240 or 400. What is the smallest positive integer that she could have ended with? | Answer |
| 6. | How many 4-digit integers are there whose digits are all non-zero and whose digits add up to 7? | Answer |
| 7. | How many positive integers are there whose digits are all non-zero and whose digits add up to 7? | Answer |
| 8. | Eve wrote down a four-digit number. Eve then removed one of the digits of her number to make a three-digit number. The sum of her two numbers is 3119. What was her four-digit number? | Answer |
| 9. | Eve wrote down a five-digit number. Eve then removed one of the digits of her number to make a four-digit number. The sum of her two numbers is 96158. What is the largest number that her five-digit number could have been? | Answer |
| 10. | Noel drew 12 points on the circumference of a circle, then drew a straight line connecting every pair of points. How many lines did he draw? | Answer |
| 11. | Noel drew some points on the circumference of a circle, then drew a straight line connecting every pair of points. He drew 2926 lines. How many points did he draw? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Great fun thanks. At first they seem impossible but then a way through appears! How do I get the answers / check if I’m right?
Graeme Johnston
Add a Comment