Blog
2022-10-27
It's a while since I've put a new blog post here. This is partly because I've been busy working on other exciting maths projects. One of these exciting projects
is happening tomorrow: the 24 Hour Maths Game Show.
Two years ago, I helped run the 24 Hour Maths Magic Show. Two years on, we've decided to do it again, but this time
the show will feature 24 hours of content about games, including mathematical game shows, game theory, board games, and video games. The full schedule for the show is
at 24hourmaths.com/gameshow, and you can watch it for free on YouTube.
If for some reason you want to just watch the bits featuring me, I'll be on the show doing the following (all times in BST/UTC+1):
- From 7pm on Friday, I'll be on the stream with the rest of the team opening the show
- From 7:30pm on Friday, I'll be chatting to James Grime about adventure game books
- From 1:30am on Saturday, I'll be talking with Katie Steckles about Pac-Man
- From 10:30am on Saturday, I'll be hosting The Unbelievable Proof, a panel game where the contestant present two-minute lectures that are entirely false except for five hidden truths, while the other contestants try to spot the truths
- From 5pm on Saturday, I'll be hosting Jeopardy! with Adam Townsend
- From 6pm on Saturday, I'll be reacting to tasks people have been attempting during the Taskmathster segment
I'd recommend watching as much of the show as you can; the whole thing is going to be amazing. A recording of the whole thing will be available afterwards if you can't stay away for the whole lot.
The show is raising money for four excellent charities, so throw some money their way if you enjoy the show.
After you've watched the show, keep an eye out for the next issue of Chalkdust, which is due out in the next few weeks. And it's not long until there'll be a post here about this year's Advent calendar...
Edit: Added links to watch recordings of each segment.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2022-03-14
A few weekends ago, I visited Houghton-le-Spring
to spend two days helping with an attempt to compute the first 100 decimal places of π by hand. You can watch Matt Parker's video about our
calculation to find out about our method and how many correct decimal places we achieved.
Spending two days computing an approximation of π led me to wonder how accurate
calculations using various approximations of π would be.
One nice way to visualise this is to ask: what is the largest circle
whose area can be correctly computed to the nearest mm² when using a chosen approximation of π? In this
blog post, I'll answer this question for a range of approximations of π.
3
First up, how about the least accurate approximation we could possibly use: π = 3.
Using this approximation, the areas of circles with a radius of up to 1.88mm could be calculated
correctly to the nearest mm². That's a circle about the size of an ant.
Today is Pi Day, as in the date format M.DD, today's date is the first three digits of π.
Using this approximation, circles with a radius of up to 17.7mm or 1.77cm can be calculated correctly
to the nearest mm². That's a circle about the size of my thumb.
In the date format DD/M, 22 July gives an approximation of π that is more accurate than 3.14.
Using this approximation, circles with a radius of up to 19.8mm or 1.98cm can be calculated correctly
to the nearest mm². That's a slightly bigger circle that's still about the size of my thumb.
In Houghton-le-Spring, our final computed value was 3.1415926535886829815214...
The first 11 decimal places of this are correct.
Using this approximation, circles with a radius of up to \(6.71\times10^5\)mm or 671m can be calculated correctly
to the nearest mm². That's a circle about the size of Regent's park.
The 100 decimal places we were aiming for
If we'd avoided any mistakes in Hougton-le-Spring, we would've obtained the first 100 decimal places
of π. Using the first 100 decimal places of π, circles with a radius of up to \(7.8\times10^9\)mm
or 7800km can be calculated correctly
to the nearest mm². That's a circle just bigger than the Earth.
In 1873, William Shanks computed 707 decimal places of π in Houghton-le-Spring. His first 527
decimal places were correct. Using his approximation, circles with a radius of up to approximately
\(10^{263}\)mm
or \(10^{244}\) light years can be calculated correctly
to the nearest mm². The observable universe is only around \(10^{10}\) light years wide.
That's a quite big circle.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
I wonder if energy can be put into motion with pi, so that would be a lot of theoretical energy
Willem
Add a Comment
2022-02-26
Surprisingly often, people ask me how they can build their own copy of MENACE. If you've been thinking that you'd love your own matchbox-powered machine learning computer but haven't got round to asking me about it yet, then this blog post is just what you're looking for.
Matchboxes
Before building MENACE, you'll need to get hold of 304 matchboxes (plus a few spares in case one gets lost or falls apart). I used these craft matchboxes: they don't have the best build quality, but they're good enough.
304 positions
The positions you need to glue onto the front of the matchboxes can be downloaded from this GitHub repository (first move boxes, third move boxes, fifth move boxes, seventh move boxes). These are sized to fit on matchboxes that have 15mm by 35mm fronts.
I printed each pdf on differently coloured paper to make it easier to sort the matchboxes after getting them out of their box.
If you get differently sized matchboxes, the code used the generate the PDFs is in the same GitHub repository (you'll need to modify these lines). Alternatively, feel free to drop me an email and I will happily adjust the sizes for you and send you the updated PDFs.
Glue
I used PVA glue to stick the positions onto the matchboxes. The printable PDFs have extra tabs of paper above and below the postions that can be glued in to the bottom and inside of the matchbox tray to hold it more securely.
Gluing the positions onto the matchboxes was the most time consuming part of building my copy of MENACE, largely due to having to wait for the glue to dry on a set of matchboxes before I had space for the next batch of them to dry.
Beads
Once you've glued pictures of noughts and crosses positions to 304 matchboxes, you'll need to put coloured beads into each matchbox. For this, I used a large tub of Hama beads (that tub contained orders of magnitude more beads than I needed).
A nice side effect of using Hama beads is that they're designed to be ironed together so making a key to show which colour corresponds to each position is very easy.
I typically start the boxes off with 8 beads of each colour in the first move box, 4 of each colour in the third move boxes, 2 of each in the fifth move boxes, and one of each in the seventh move boxes.
Once you've filled all your matchboxes with the correct number of beads, you're ready to play yout first game against MENACE. I'd love to hear how you get on.
And once you're bored of playing noughts and crosses against your matchboxes, why not build a machine that learns to play Hexapawn, Connect 4, Chess or Go? Or one that plays Nim?
Edit: Added link to the printable pdfs of the positions needed for Hexapawn, made by Dan Whitman.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Interesting.
Could try a same kind of thing using playing card deck(s)? A(=1)-2-3 4-5-6 7-8-9 maybe 3 decks with different colours on their backs.
Could try a same kind of thing using playing card deck(s)? A(=1)-2-3 4-5-6 7-8-9 maybe 3 decks with different colours on their backs.
Willem
I also read the Martin Gardner article way back when and had two matchbox machines (actually with envelopes instead of matchboxes) play Nim against each other. I don't remember all the details now, except that it got to the point where one would make the first move and the other would immediately resign.
Tim Lewis
I made a matchbox machine that learns to play 3x3 Nim almost 50 years ago. I still have it. (Based on Martin Gardner's article)
Tony
Add a Comment
2022-01-08
Welcome to 2022 everyone! Now that the Advent calendar has disappeared, it's time to reveal the answers and annouce the winners.
But first, some good news: with your help, a successful test flight was made and Christmas was saved!
Now that the competition is over, the questions and all the answers can be found here.
Before announcing the winners, I'm going to go through some of my favourite puzzles from the calendar, reveal the solution and a couple of other interesting bits and pieces.
Highlights
My first highlight is the puzzle from 2 December. I like this puzzle, as it's very difficult (maybe impossible) to work out by
brute force (as \(n\) is a huge number), and the solution method I used was satisfying.
2 December
The number \(7n\) has 37 factors (including 1 and the number itself). How many factors does \(8n\) have?
There was a typo in this puzzle. It originally read "38 factors" when it was meant to say "37 factors".
My next hightlight is the puzzle from 5 December. It's difficult to find many triangles with
perimeter 50 and an integer area, but there's a neat way to solve this without needing to find any.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
My next highlight is the puzzle from 14 December. This is closely related to the puzzle
from 12 December but this time movements to the left are allowed.
I enjoyed a nice "aha!" moment when designing this puzzle.
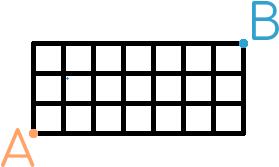
14 December
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right, upwards, or to the left along the black lines, but you cannot pass along the same line segment more than once.
Today's number is the total number of possible routes to get from A to B.
My final highlight is the puzzle from 16 December. If you enjoyed this one, you'll
probably also enjoy the crossnumber I wrote for Chalkdust issue 13.
16 December
Each clue in this crossnumber is formed of two parts connected by a logical connective:
and means that both parts are true;
nand means that at most one part is true;
or means that at least one part is true;
nor means that neither part is true;
xor means that exactly one part is true;
xnor means that either both parts are false or both parts are true.
No number starts with 0.
|
1A is a palindrome xnor 1D is a palindrome.
1A is greater than 350 nor 1D is less than 150.
3D is odd nand 4A and 2D are equal.
3D is prime xor 5A is odd.
4A is a cube and 2D is a cube.
The sum of the digits of 3D is 2 or the sum of the digits of 5A is 5.
Today's number is 1D.
|
Hardest and easiest puzzles
Once you've entered 24 answers, the calendar checks these and tells you how many are correct. I logged the answers that were sent
for checking and have looked at these to see which puzzles were the most and least commonly incorrect. The bar chart below shows the total number
of incorrect attempts at each question.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Day | |||||||||||||||||||||||
You can see that the most difficult puzzles were those on
5 and
14 December;
and the easiest puzzles were on
6,
8, and
9 December.
An Easter egg
The numbers on the doors of the Advent calendar formed a magic square: the numbers in each row, each
column, and on the two major diagonals all add up to the same total.
This was spotted by
both Colin Beveridge (@icecolbeveridge)
and Alex on 15 December.
The winners
And finally (and maybe most importantly), on to the winners: 150 people solved all the puzzles and made a successful test flight. That's down on last year but up on two years ago:
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 |
| Year | ||||||
From the correct answers, the following 10 winners were selected:
- Shivanshi
- LycanFayn
- Colin Beveridge
- Katharine Velleman
- Gregory Wheeler
- Alex Bolton
- Don Anderson
- Dan Colestock
- Pamela Docherty
- Annabel
Congratulations! Your prizes will be on their way shortly.
The prizes this year include 2021 Advent calendar T-shirts. If you didn't win one, but would like one of these, I've made them available to buy at merch.mscroggs.co.uk alongside the T-shirts from previous years.
Additionally, well done to
Aaron Stiff, Alan Buck, Alanis, Alek2ander, Alex, Alex Davis, Andrew Brady, Andrew Roy, Andrew Turner, Austin,
B Moreland, Becky Russell, Ben Baker, Ben Boxall, Ben Jones, Ben Reiniger, Ben Tozer, Berl Steiner, Brennan Dolson, Brian Carnes, Brian Wellington,
Carl Westerlund, Carmen, Cathy Hooper, Chris Hellings, Christopher Adams, Christy Hales, Connie, Corbin Groothuis, CreativeCrocheter,
Dan DiMillo, Dan Whitman, Daniel Chiverton, Daniel Low, Dave Budd, David Ault, David Berardo, David Fox, David Kendel, David Mitchell, David P, David and Ivy Walbert, Deborah Tayler, Dylan Madisetti,
Elijah Kuhn, Emily Troyer, Eric, Eric Kolbusz, Erik Eklund,
Frank Kasell, Franklin Ta, Fred Verheul,
Gabriella Pinter, Gary M. Gerken, Gert-Jan de Vries, Gregory Loges, Gwendolenn,
Hannah , Harry Allen, Heerpal Sahota, Helen, Helen Bradley, Håkon Balteskard,
Iris,
Jacob Y, James Chapman, Jarvis, Jay Miller, Jean-Noël Monette, Jean-Sébastien Turcotte, Joe Gage, John Alasdair Warwicker, Jon Palin, Jonathan Chaffer, Jonathan Winfield, Jorge del Castillo, Joseph Wagner,
Kai, Karen Climis, Kim Brooks, Kristen Koenigs,
Lauren Woolsey, Lemminkäinen, Lewis Dyer, Liz Madisetti, Louis, Luke S,
Maggie Orr, Magnus Eklund, Marco van der Park, Maria, Mark Stambaugh, Martin Harris, Martin Holtham, Matt Askins, Matthew, Matthew Schulz, Mels, Michael DeLyser, Mihai Zsisku, Mike Hands, Millie,
NIck C, Nadine Chaurand, Naomi Bowler, Nick Keith, Niji, Nikos I., Noah Overcash,
Oscar, Friend of Rudolph,
patrick fussell,
Ray Arndorfer, Rea, Reuben Cheung, Riccardo Lani, Rick Simineo, Robert Brady, Roger Lipsett, Rosie Paterson, Russ Collins, Ruth, Ryan W,
Scott, Sean Carmody, Sean Henderson, Seth Cohen, SherlockSage, Simon Schneider,
Tamara Brenner, Tarim, Tom Fryers, Tony Mann, tripleboleo, Tristan S,
UsrBinPRL,
Valentin VĂLCIU, Vinayak,
Yasha, Yuliya Nesterova, and Yurie Ito,
who all also completed the Advent calendar but were too unlucky to win prizes this time or chose to not enter the prize draw.
See you all next December, when the Advent calendar will return.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
I feel compelled to admit that something over a hundred of the checks on day 14 were me after I gave up all hope of figuring out the elegant solution and just started counting up from what I had come up with as a lower limit. I really, really wanted a go at the logic puzzle.
At least my failed attempt to figure that one made me realize that I needed to change my answer to day 12.
At least my failed attempt to figure that one made me realize that I needed to change my answer to day 12.
Kim
Damn, missed out again! But had a lot of fun (again). I'd guess the reason for there being fewer successful entries this year was the final puzzle being much harder than previous years, rather than a drop in participation. I got worried I still hadn't solved it on the 30th and had to get my whole family involved!
Louis
Thanks for the advert calendar this year.
By the way, in the "Hardest and easiest puzzles" section, 4 out of the 5 links to the puzzles are to the 2020 puzzles instead of the 2021 puzzles
By the way, in the "Hardest and easiest puzzles" section, 4 out of the 5 links to the puzzles are to the 2020 puzzles instead of the 2021 puzzles
Alex
My son and I really enjoyed solving the puzzles each day. As a mom whose son is thousands of miles away, it was a great way to connect each day of Advent. This is our second year and I will definitely order a tee shirt. Keep up the great work!
Liz
Add a Comment
2021-12-04
In November, I spent some time designing this year's Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 14 puzzles. By writing the answers to the puzzles in the triangles on the front of the card, then colouring triangles containing 1s, 2s, 5s or 6s in the right colour, you will reveal a Christmas themed picture.
If you want to try the card yourself, you can download this printable A4 pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will automatically be written in the triangles, and the triangles will be coloured...
The puzzles | ||
| 1. | What is the sum of all the odd integers between 0 and 30? | Answer |
| 2. | What is the sum of all the odd integers between 0 and 5668? | Answer |
| 3. | What is the smallest integer with a digital sum of 28 and a digital product of 10000? | Answer |
| 4. | What is the smallest integer with a digital sum of 41 and a digital product of 432000? | Answer |
| 5. | What is the area of the largest area dodecagon that will fit inside a circle with area \(111185\pi\)? | Answer |
| 6. | What is the area of the largest area heptagon that will fit inside a semicircle with area \(115185\pi\)? | Answer |
| 7. | How many terms are there in the (simplified) expansion of \((x+y+z)^{2}\)? | Answer |
| 8. | How many terms are there in the (simplified) expansion of \((x+y+z)^{41172}\)? | Answer |
| 9. | What is the largest integer that cannot be written as \(4a+5b\) for non-negative integers \(a\) and \(b\)? | Answer |
| 10. | What is the largest integer that cannot be written as \(83409a+66608b\) for non-negative integers \(a\) and \(b\)? | Answer |
| 11. | How many positive integers are there below 100 whose digits are all non-zero and different? | Answer |
| 12. | How many positive integers are there whose digits are all non-zero and different? | Answer |
| 13. | What is the only integer for which taking the geometric mean of all its factors (including 1 and the number itself) gives 2? | Answer |
| 14. | What is the only integer for which taking the geometric mean of all its factors (including 1 and the number itself) gives 25? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@HJ: the smallest one does have 6, and Q4 is correct too. I bought the cards and had good fun solving it myself. I’m glad to find this here though to check my answers as when I did the shading it looked like the picture wasn’t quite right. Thanks for the cards Matthew, I look forward to next year’s - no pressure!
Alec
The only one I'm stuck on is #6. I thought I was doing it right but I'm getting a non-integer answer. I'm assuming the heptagon in question is aligned so one of its sides sits on the diameter of the semicircle, and the opposite vertex sits on the curved edge of the semicircle. Is this wrong?
Seth C
The version of the card on this page doesn't check if your answers are correct, so it will colour in any number you enter as long as it has the right number of digits.
Matthew
Wonky solution for #9? On a blank start page, answering "16" gives you red and white puzzle completions, yet we _know_ that 16 is an incorrect answer. Strange?
Attika
Add a Comment