Advent calendar 2021
Advent 2021 logic puzzle
It's nearly Christmas and something terrible has happened: a saboteur has infiltrated the stables where Santa's reindeer are kept, and has caused all three of Santa's test flights to be unsuccessful.
You need to help Santa have a successful test flight so that he can deliver presents before Christmas is ruined for everyone.
In order to have enough magical power to fly with the sleigh, all nine of Santa's reindeer must be fed their favourite food. The saboteur gave one or more reindeer the wrong food before each of
the three test flights, causing the reindeer to be unable to take off.
In each clue, "before test flight n" means "immediately before test flight n". Before each test flight, each reindeer was fed exactly one
food, and two or more reindeer may have been fed the same food. Two or more reindeer may have the same favourite food. You must use these clues to work out what each reindeer's favourite food is, then complete a test flight by feeding each reindeer the correct food.
11
Before test flight 2, reindeer 9 was given food 5.
18
Before test flight 2, reindeer 8 was given food 2
2
Before test flight 1, reindeer 2 was given food 4.
9
Before test flight 1, 2 reindeer were given the wrong food.
10
Before test flight 1, reindeer 9 was given food 6
12
Before test flight 3, reindeer 9 was given food 1
19
Before test flight 3, reindeer 5 was not given food 7
21
Before test flight 3, reindeer 7 was given food that is a factor of 148
3
Before test flight 2, reindeer 2 was given food 4.
4
Before test flight 3, reindeer 2 was given food 6.
6
Reindeer 4's favourite food is a factor of 607
13
Before test flight 2, reindeer 4 was not given food 9
20
Before test flight 3, 3 reindeer had the food equal to their number
22
Before test flight 3, reindeer 7 was not given food 1
23
Before test flight 3, no reindeer was given food 2
5
Before test flight 3, 4 reindeer were given the wrong food.
7
Reindeer 4 was given the same food before all three test flights.
14
Before test flight 2, 2 reindeer were given the wrong food
16
Before test flight 2, all the reindeer were given different foods
17
Before test flight 1, reindeer 7 was not given food 7
24
Before test flight 1, reindeer 7 was not given food 9
1
Reindeer 2's favourite food is 4
8
Before test flight 1, reindeer 8 was given food 3.
15
Reindeer 1 was given food 1 before all three test flights
You can attempt a test flight here.
24 December
The digital product of a number is computed by multiplying together all of its digits.
For example, the digital product of 1522 is 20.
How many 12-digit numbers are there whose digital product is 20?
23 December
I draw the parabola \(y=x^2\) and mark points on the parabola at \(x=17\) and \(x=-6\).
I then draw a straight line connecting these two points.
At which value of \(y\) does this line intercept the \(y\)-axis?
22 December
There are 12 ways of placing 2 tokens on a 2×4 grid so that no two tokens are next to each other horizontally, vertically or diagonally:
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Today's number is the number of ways of placing 2 tokens on a 2×21 grid so that no two tokens are next to each other horizontally, vertically or diagonally.
21 December
Arrange the digits 1–9 (using each digit exactly once) so that the three digit number in:
the middle row is a prime number;
the bottom row is a square number;
the left column is a cube number;
the middle column is an odd number;
the right column is a multiple of 11.
The 3-digit number in the first row is today's number.
| today's number | |||
| prime | |||
| square | |||
| cube | odd | multiple of 11 |
20 December
What is the area of the largest area triangle that has one side of length 32 and one side of length 19?
19 December
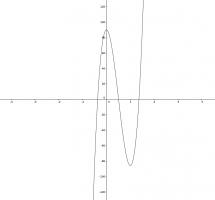
The equation \(352x^3-528x^2+90=0\) has three distinct real-valued solutions.
Today's number is the number of integers \(a\) such that the equation
\(352x^3-528x^2+a=0\) has three distinct real-valued solutions.
18 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | + | = 11 | |||
| + | × | × | |||
| + | + | = 17 | |||
| × | - | + | |||
| + | + | = 17 | |||
| = 11 | = 17 | = 17 |
17 December
The digital product of a number is computed by multiplying together all of its digits.
For example, the digital product of 6273 is 252.
Today's number is the smallest number whose digital product is 252.
16 December
Each clue in this crossnumber is formed of two parts connected by a logical connective:
and means that both parts are true;
nand means that at most one part is true;
or means that at least one part is true;
nor means that neither part is true;
xor means that exactly one part is true;
xnor means that either both parts are false or both parts are true.
No number starts with 0.
|
1A is a palindrome xnor 1D is a palindrome.
1A is greater than 350 nor 1D is less than 150.
3D is odd nand 4A and 2D are equal.
3D is prime xor 5A is odd.
4A is a cube and 2D is a cube.
The sum of the digits of 3D is 2 or the sum of the digits of 5A is 5.
Today's number is 1D.
|
15 December
The odd numbers are written in a pyramid.
| (row 1) | 1 | ||||
| (row 2) | 3 | 5 | |||
| (row 3) | 7 | 9 | 11 | ||
| etc. | |||||
What is the mean of the numbers in the 19th row?
14 December
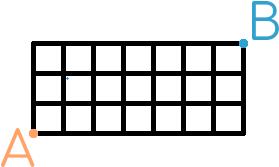
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right, upwards, or to the left along the black lines, but you cannot pass along the same line segment more than once.
Today's number is the total number of possible routes to get from A to B.
13 December
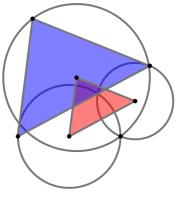
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
12 December
You start at the point marked A in the picture below. You want to get to the point marked B. You may travel to the right or upwards along the black lines.
Today's number is the total number of possible routes to get from A to B.
11 December
The integers are written in a triangle as shown below:
| 1 | ||||||
| 2 | 3 | 4 | ||||
| 5 | 6 | 7 | 8 | 9 | ||
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| etc. | ||||||
Today's number appears directly above the number 750 in the triangle of integers.
10 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct.
Today's number is the largest number you can make using the digits in the red boxes.
| + | + | = 20 | |||
| + | + | + | |||
| + | + | = 10 | |||
| + | + | + | |||
| + | + | = 15 | |||
| = 7 | = 23 | = 15 |
9 December
Eve writes down a sequence of consecutive positive integers (she writes more than one number). The sum of the numbers Eve has written down is 844.
Today's number is the smallest integer that Eve has written down.
8 December
The sum of three integers is 51. The product of the same three integers is 836. What is the product of largest integer and the second-largest integer?
7 December
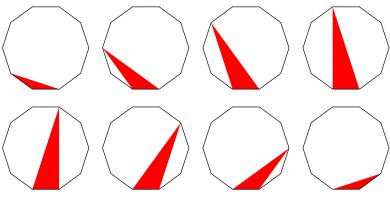
The picture below shows eight regular decagons. In each decagon, a red triangle has been drawn with vertices at three of the vertices of the decagon.
The area of each decagon is 240. What is the total area of all the red triangles?
6 December
When 12345 is divided by today's number, the remainder is 205. When 6789 is divided by today's number, the remainder is 112.
5 December
How many different isosceles triangles are there whose perimeter is 50 units, and whose area is an integer number of square-units?
(Two triangles that are rotations, reflections and translations of each other are counted as the same triangle. Triangles with an area of 0 should not be counted.)
4 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| + | - | = 5 | |||
| ÷ | × | × | |||
| + | - | = 5 | |||
| - | ÷ | ÷ | |||
| + | × | = 10 | |||
| = -6 | = 18 | = 35 |
3 December
If you write out the numbers from 1 to 1000 (inclusive), how many times will you write the digit 0?
2 December
The number \(7n\) has 37 factors (including 1 and the number itself). How many factors does \(8n\) have?
There was a typo in this puzzle. It originally read "38 factors" when it was meant to say "37 factors".
1 December
The geometric mean of a set of \(n\) numbers can be computed by multiplying together all the numbers then computing the \(n\)th root of the result.
The factors of 4 are 1, 2 and 4. The geometric mean of these is 2.
The factors of 6 are 1, 2, 3, and 6. The geometric mean of these is \(\sqrt{6}\).
The geometric mean of all the factors of today's number is 22.