Blog
2018-03-22
Back in 2014, I worked out the cost of filling an official Panini World Cup 2014 sticker book. Today, the 2018 sticker book was relased: compared to four years ago, there are more stickers to collect and the prices have all changed. So how much should we expect it to cost us to fill the album this time round?
How many stickers will I need?
There are 682 stickers to collect. Imagine you have already stuck \(n\) stickers into your album. The probability that the next sticker you buy is new is
$$\frac{682-n}{682}.$$
The probability that the second sticker you buy is the next new sticker is
$$\mathbb{P}(\text{next sticker is not new})\times\mathbb{P}(\text{sticker after next is new})$$
$$=\frac{n}{682}\times\frac{682-n}{682}.$$
Following the same method, we can see that the probability that the \(i\)th sticker you buy is the next new sticker is
$$\left(\frac{n}{682}\right)^{i-1}\times\frac{682-n}{682}.$$
Using this, we can calculate the expected number of stickers you will need to buy until you find a new one:
$$\sum_{i=1}^{\infty}i \left(\frac{682-n}{682}\right) \left(\frac{n}{682}\right)^{i-1} = \frac{682}{682-n}$$
Therefore, to get all 682 stickers, you should expect to buy
$$\sum_{n=0}^{681}\frac{682}{682-n} = 4844 \text{ stickers}.$$
How much will this cost?
You can buy the following [source]:
- Starter pack (an album and 31 stickers) for £3.99
- Sticker packs (5 stickers) for 80p
- Sticker multipacks (30 stickers) for £4.50
First of all you'll need to buy the starter pack, as you need an album to stick everything in. This comes with 31 stickers; we should expect to buy 4813 more stickers after this.
The cheapest way to buy these stickers is to buy them in multipacks for 15p per sticker. This gives a total expected cost of filling the sticker album of £725.94. (Although if your local newsagent doesn't stock the multipacks, buying 80p packs to get these stickers will cost you £774.07.)
What if I order the last 50 stickers?
If you'd like to spend a bit less on the sticker book, Panini lets you order the last 50 stickers to complete your album. This is very helpful as these last 50 stickers are the most expensive.
You can order missing stickers from the Panini website for 22p per sticker's sticker ordering service for the 2018 World Cup doesn't appear to be online yet; but based on other recent collections, it looks like ordered stickers will cost 16p each, with £1 postage per order.
Ordering the last 50 stickers reduces the expected number of other stickers you need to buy to
$$\sum_{n=0}^{631}\frac{682}{682-n} = 1775 \text{ stickers}.$$
This reduces the expected overall cost to £291.03. So I've just saved you £434.91.
What if I order more stickers?
Of course, if you're willing to completely give up on your morals, you could order more than one batch of 50 stickers from Panini. This raises the question: how many should you order to minimise the expected cost.
If you order the last \(a\) stickers, then you should expect to pay:
- £3.99 for the album and first 31 stickers
- £\(\displaystyle0.15\left(\sum_{n=1}^{681-a}\frac{682}{682-n}-31\right)\) for other stickers you need
- £\(\displaystyle \left(0.16a+\left\lceil \frac{a}{50}\right\rceil\right)\) to order the last \(a\) stickers
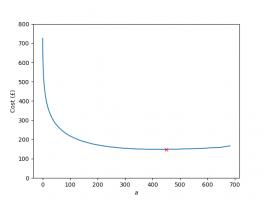
The total expected cost of filling your album for different values of \(a\) is shown in the graph below.
The red cross shows the point at which the album is cheapest: this is when the last 550 stickers are ordered, giving a total expected cost of £120.18. That's another £170.85 I've saved you. You're welcome.
Still, ordering nearly all stickers to minimise the cost doesn't sound like the most fun way to complete the sticker book, so you probably need to order a few less than this to maximise your fun.
What about swaps?
Of course, you can also get the cost of filling the book down by swapping your spare stickers with friends. In 2016, I had a go at simulating filling a sticker book with swapping and came to the possibly obvious conclusion that the more friends you have to swap with, the cheaper filling the book will become.
My best advice for you, therefore, is to get out there right now and start convinding your friends to join you in collecting stickers.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Helpful article!! My head always go into a spine with probability, but does the fact that you would not get a double within a pack affect the overall strategy or cost? My head says this is an another advantage of buying 30 packs over the 5.
RM
Add a Comment
2015-10-08
This post also appeared on the Chalkdust Magazine blog. You can read the excellent second issue of Chalkdust here, including the £100 prize crossnumber which I set.
From today, the National Lottery's Lotto draw has 59 balls instead of 49. You may be thinking that this means there is now much less chance of winning. You would be right, except the prizes are also changing.
Camelot, who run the lottery, are saying that you are now "more likely to win a prize" and "more likely to become a millionaire". But what do these changes actually mean?
The changes
Until yesterday, Lotto had 49 balls. From today, there are 59 balls. Each ticket still has six numbers on it and six numbers, plus a bonus ball, are still chosen by the lottery machine. The old prizes were as follows:
| Requirement | Estimated Prize |
| Match all 6 normal balls | £2,000,000 |
| Match 5 normal balls and the bonus ball | £50,000 |
| Match 5 normal balls | £1,000 |
| Match 4 normal balls | £100 |
| Match 3 normal balls | £25 |
| 50 randomly picked tickets | £20,000 |
The prizes have changed to:
| Requirement | Estimated Prize |
| Match all 6 normal balls | £2,000,000 |
| Match 5 normal balls and the bonus ball | £50,000 |
| Match 5 normal balls | £1,000 |
| Match 4 normal balls | £100 |
| Match 3 normal balls | £25 |
| Match 2 normal balls | Free lucky dip entry in next Lotto draw |
| One randomly picked ticket | £1,000,000 |
| 20 other randomly picked tickets | £20,000 |
Probability of Winning a Prize
The probability of winning each of these prizes can be calculated. For example, the probability of matching all 6 balls in the new lotto is $$\mathbb{P}(\mathrm{matching\ ball\ 1})\times \mathbb{P}(\mathrm{matching\ ball\ 2})\times...\times\mathbb{P}(\mathrm{matching\ ball\ 6})$$ $$=\frac{6}{59}\times\frac{5}{58}\times\frac{4}{57}\times\frac{3}{56}\times\frac{2}{55}\times\frac{1}{54}$$ $$=\frac{1}{45057474},$$ and the probability of matching 4 balls in the new lotto is $$(\mathrm{number\ of\ different\ ways\ of\ picking\ four\ balls\ out\ of\ six})\times\mathbb{P}(\mathrm{matching\ ball\ 1})\times\\...\times\mathbb{P}(\mathrm{matching\ ball\ 4})\times\mathbb{P}(\mathrm{not\ matching\ ball\ 5})\times\mathbb{P}(\mathrm{not\ matching\ ball\ 6})$$ $$=15\times\frac{6}{59}\times\frac{5}{58}\times\frac{4}{57}\times\frac{3}{56}\times\frac{53}{55}\times\frac{52}{54}$$ $$=\frac{3445}{7509579}.$$ In the second calculation, it is important to include the probabilities of not matching the other balls to prevent double counting the cases when more than 4 balls are matched.
Calculating a probability for every prize and then adding them up gives the probability of winning a prize. In the old draw, the probability of winning a prize was \(0.0186\). In the new draw, it is \(0.1083\). So Camelot are correct in claiming that you are now more likely to win a prize.
But not all prizes are equal: these probabilities do not take into account the values of the prizes. To analyse the actual winnings, we're going to have to look at the expected amount of money you will win. But first, let's look at Camelot's other claim: that under the new rules you are more likely to become a millionaire.
Probability of winning £1,000,000
In the old draw, the only way to win a million pounds was to match all six balls. The probability of this happening was \(0.00000007151\) or \(7.151\times 10^{-8}\).
In the new lottery, a million pounds can be won either by matching all six balls or by winning the millionaire raffle. This will lead to different probabilities of winning on Wednesdays and Saturdays due to different numbers of people buying tickets. Based on expected sales of 16.5 million tickets on Saturdays and 8.5 million tickets on Wednesdays, the chances of becoming a millionaire on a Wednesday or Saturday are \(0.0000001398\) (\(1.398\times 10^{-7}\)) and \(0.00000008280\) (\(8.280\times 10^{-8}\)) respectively.
These are both higher than the probability of winning a million in the old draw, so again Camelot are correct: you are now more likely to become a millionaire...
But the new chances of becoming a millionaire are actually even higher. The probabilities given above are the chances of winning a million in a given draw. But if two balls are matched, you win a lucky dip: you could win a million in the next draw without buying another ticket. We should include this in the probability calculated above, as you are still becoming a millionaire due to the original ticket you bought.
In order to count this, let \(A_W\) and \(A_S\) be the probabilities of winning a million in a given draw (as given above) on a Wednesday or a Saturday, let \(B_W\) and \(B_S\) be the probabilities of winning a million in this draw or due to future lucky dip tickets on a Wednesday or a Saturday (the values we want to find) and let \(p\) be the probability of matching two balls. We can write $$B_W=A_W+pB_S$$ and $$B_S=A_S+pB_W$$ since the probability of winning a million is the probability of winning in this draw (\(A\)) plus the probability of winning a lucky dip ticket and winning in the next draw (\(pB\)). Substituting and rearranging, we get $$B_W=\frac{A_W+pA_S}{1-p^2}$$ and $$B_W=\frac{A_S+pA_W}{1-p^2}.$$
Using this (and the values of \(A_S\) and \(A_W\) calculated earlier) gives us probabilities of \(0.0000001493\) (\(1.493\times 10^{-7}\)) and \(0.00000009736\) (\(9.736\times 10^{-8}\)) of becoming a millionaire on a Wednesday and a Saturday respectively. These are both significantly higher than the probability of becoming a millionaire in the old draw (\(7.151\times 10^{-8}\)).
Camelot's two claims—that you are more likely to win a prize and you are more likely to become a millionaire—are both correct. It sounds like the new lottery is a great deal, but so far we have not taken into account the size of the prizes you will win and have only shown that a very rare event will become slightly less rare. Probably the best way to measure how good a lottery is is by working out the amount of money you should expect to win, so let's now look at that.
Expected prize money
To find the expected prize money, we must multiply the value of each prize by the probability of winning that prize and then add them up, or, in other words,
$$\sum_\mathrm{prizes}\mathrm{value\ of\ prize}\times\mathbb{P}(\mathrm{winning\ prize}).$$
Once this has been calculated, the chance of winning due to a free lucky dip entry must be taken into account as above.
In the old draw, after buying a ticket for £2, you could expect to win 78p or 83p on a Wednesday or Saturday respectively. In the new draw, the expected winnings have changed to 58p and 50p (Wednesday and Saturday respectively). Expressed in this way, it can be seen that although the headline changes look good, the overall value for money of the lottery has significantly decreased.
Looking on the bright side, this does mean that the lottery will make even more money that it can put towards charitable causes: the lottery remains an excellent way to donate your money to worthy charities!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2014-04-11
As well as letters games, the contestants on Countdown also take part in numbers games. Six numbers are chosen from the large numbers (25,50,75,100) and small numbers (1-10, two cards for each number) and a total between 101 and 999 (inclusive) is chosen by CECIL. The contestants then use the six numbers, with multiplication, addition, subtraction and division, to get as close to the target number as possible.
The best way to win the numbers game is to get the target exactly. This got me wondering: is there a combination of numbers which allows you to get every total between 101 and 999? And which combination of large and small numbers should be picked to give the highest chance of being able to get the target?
To work this out, I got my computer to go through every possible combination of numbers, trying every combination of operations. (I had to leave this running overnight as there are a lot of combinations!)
Getting every total
There are 61 combinations of numbers which allow every total to be obtained. These include the following (click to see how each total can be made):
- 5 6 8 9 10 100
- 5 6 7 8 10 100
- 4 6 7 8 9 100
- 3 6 7 8 10 100
- 3 5 7 8 9 100
- 2 5 6 8 9 100
- 2 6 7 8 9 100
- 5 6 8 9 75 100
- 3 6 8 10 75 100
- 2 6 9 10 75 100
By contrast, the following combination allows no totals between 101 and 999 to be reached:
- 1 1 2 2 3 3
The number of attainable targets for each set of numbers can be found here.
Probability of being able to reach the target
Some combinations of numbers are more likely than others. For example, 1 2 25 50 75 100 is four times as likely as 1 1 25 50 75 100, as (ignoring re-orderings) in the first combination, there are two choices for the 1 tile and 2 tile, but in the second combination there is only one choice for each 1 tile. Different ordering of tiles can be ignored as each combination with the same number of large tiles will have the same number of orderings.
By taking into account the relative probability of each combination, the following probabilities can be found:
| Number of large numbers | Probability of being able to reach target |
| 0 | 0.964463439 |
| 1 | 0.983830962 |
| 2 | 0.993277819 |
| 3 | 0.985770510 |
| 4 | 0.859709475 |
So, in order to maximise the probability of being able to reach the target, two large numbers should be chosen.
However, as this will mean that your opponent will also be able to reach the target, a better strategy might be to pick no large numbers or four large numbers and get closer to the target than your opponent, especially if you have practised pulling off answers like this.
Edit: Numbers corrected.
Edit: The code used to calculate the numbers in this post can now be found here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@Francis Galiegue: I've pushed a version of the code to https://github.com/mscroggs/countdown-...
Matthew
@Francis Galiegue: Sadly, I lost the code I used when I had laptop problems. However, I can remember what it did, so I shall recreate it and put it on GitHub.
Matthew
If you could, I'd love to have the code you used to do this exhaustive search?
I'm a fan of the game myself (but then I'm French, so to me it's the original, "Des chiffres et des lettres"), but for the numbers game, this is pretty much irrelevant to the language and country :)
I'm a fan of the game myself (but then I'm French, so to me it's the original, "Des chiffres et des lettres"), but for the numbers game, this is pretty much irrelevant to the language and country :)
Francis Galiegue
Add a Comment
2014-04-06
On Countdown, contestants have to make words from nine letters. The contestants take turns to choose how many vowels and consonants they would like. This got me wondering which was the best combination to pick in order to get a nine letter word.
Assuming the letters in countdown are still distributed like this, the probability of getting combinations of letters can be calculated. As the probability throughout the game is dependent on which letters have been picked, I have worked out the probability of getting a nine letter word on the first letters game.
The probability of YODELLING
YODELLING has three vowels and six consonants. There are 6 (3!) ways in which the vowels could be ordered and 720 (6!) ways in which the consonants can be ordered, although each is repeated at there are two Ls, so there are 360 distinct ways to order the consonants. The probability of each of these is:
$$\frac{21\times 13\times 13\times 6\times 3\times 5\times 4\times 8\times 1}{67\times 66\times 65\times 74\times 73\times 72\times 71\times 70\times 69}$$
So the probability of getting YODELLING is:
$$\frac{6\times 360\times 21\times 13\times 13\times 6\times 3\times 5\times 4\times 8\times 1}{67\times 66\times 65\times 74\times 73\times 72\times 71\times 70\times 69} = 0.000000575874154$$
The probability of any nine letter word
I got my computer to find the probability of every nine letter word and found the following probabilities:
| Consonants | Vowels | Probability of nine letter word |
| 0 | 9 | 0 |
| 1 | 8 | 0 |
| 2 | 7 | 0 |
| 3 | 6 | 0.000546 |
| 4 | 5 | 0.019724 |
| 5 | 4 | 0.076895 |
| 6 | 3 | 0.051417 |
| 7 | 2 | 0.005662 |
| 8 | 1 | 0.000033 |
| 9 | 0 | 0 |
So the best way to get a nine letter word in the first letters game is to pick five consonants and four vowels.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2013-12-15
Last week, I was watching Pointless and began wondering how likely it is that a show features four new teams.
On the show, teams are given two chances to get to the final—if they are knocked out before the final round on their first appearance, then they return the following episode. In all the following, I assumed that there was an equal chance of all teams winning.
If there are four new teams on a episode, then one of these will win and not return and the other three will return. Therefore the next episode will have one new team (with probability 1). If there are three new teams on an episode: one of the new teams could win, meaning two teams return and two new teams on the next episode (with probability 3/4); or the returning team could win, meaning that there would only one new team on the next episode. These probabilities, and those for other numbers of teams are shown in the table below:
| No of new teams today | |||||
Noof new teams tomorrow
| 1 | 2 | 3 | 4 | |
| 1 | 0 | 0 | \(\frac{1}{4}\) | 1 | |
| 2 | 0 | \(\frac{1}{2}\) | \(\frac{3}{4}\) | 0 | |
| 3 | \(\frac{3}{4}\) | \(\frac{1}{2}\) | 0 | 0 | |
| 4 | \(\frac{1}{4}\) | 0 | 0 | 0 | |
Call the probability of an episode having one, two, three or four new teams \(P_1\), \(P_2\), \(P_3\) and \(P_4\) respectively. After a few episodes, the following must be satisfied:
$$P_1=\frac{1}{4}P_3+P_4$$
$$P_2=\frac{1}{2}P_2+\frac{3}{4}P_3$$
$$P_3=\frac{3}{4}P_3+\frac{1}{2}P_4$$
$$P_4=\frac{1}{4}P_1$$
And the total probability must be one:
$$P_1+P_2+P_3+P_4=1$$
These simultaneous equations can be solved to find that:
$$P_1=\frac{4}{35}$$
$$P_2=\frac{18}{35}$$
$$P_3=\frac{12}{35}$$
$$P_4=\frac{1}{35}$$
So the probability that all the teams on an episode of Pointless are new is one in 35, meaning that once in every 35 episodes we should expect to see all new teams.
Edit: This blog answered the same question in a slightly different way before I got here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment



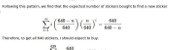




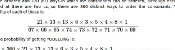
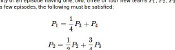


I'm not certain whether they guarantee that there are no duplicates in a pack or just it's very unlikely... Follow up post looking into this coming soon