Blog

A map projection is a way of representing the surface of a sphere, such as the Earth, on a flat surface. There is no way to represent all the features of a sphere on a flat surface, so if you want a map that shows a certain feature of the world, then you map will have to lose some other feature of the world in return.

To show you what different map projections do to a sphere, I have created a version of the game Asteroids on a sphere. I call it Mathsteroids. You can play it here, or follow the links below to play on specific projections.

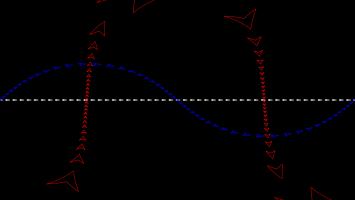
The most commonly used map projection is the Mercator projection, invented by Gerardus Mercator in 1569. The Mercator projection preserves angles: if two straight lines meet at an angle \(\theta\) on a sphere, then they will also meet at an angle \(\theta\) on the map. Keeping the angles the same, however, will cause the straight lines to no longer appear straight on the map, and the size of the same object in two different place to be very different.

The angle preserving property means that lines on a constant bearing (eg 030° from North) will appear straight on the map. These constant bearing lines are not actually straight lines on the sphere, but when your ship is already being buffeted about by the wind, the waves, and the whims of drunken sailors, a reasonably straight line is the best you can expect.

The picture below shows what three ships travelling in straight lines on the sphere look like on a Mercator projection.

To fully experience the Mercator projection, you can play Mathsteroids in Mercator projection mode here. Try flying North to see your spaceship become huge and distorted.

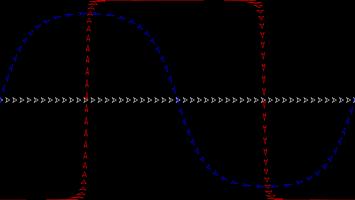
The Gall–Peters projection (named after James Gall and Arno Peters) is an area-preserving projection: objects on the map will have the same area as objects on the sphere, although the shape of the object on the projection can be very different to its shape on the sphere.

The picture below shows what three spaceships travelling in straight lines on a sphere look like on the Gall–Peters projection.

You can play Mathsteroids in Gall–Peters projection mode here. I find this one much harder to play than the Mercator projection, as the direction you're travelling changes in a strange way as you move.

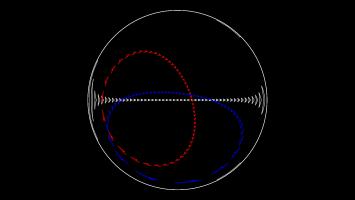
An azimuthal projection makes a map on which the directions from the centre point to other points on the map are the same as the directions on the sphere. A map like this could be useful if, for example, you're a radio operator and need to quickly see which direction you should point your aerial to communicate with other points on the map.

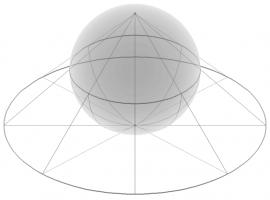
The azimuthal projection I've used in Mathsteroids also preserves distances: the distance from the centre to the another points on the map is proportional to the actual distance on the sphere. This projection is used as the emblem of the UN.

The picture below shows three straight lines on this projection. You can play Mathsteroids in azimuthal mode here.

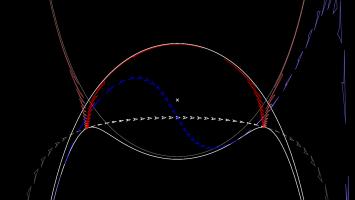
A retroazimuthal projection makes a map on which the directions to the centre point from other points on the map are the same as the directions on the sphere. If you're thinking that this is the same as the azimuthal projection, then you're too used to doing geometry on flat surfaces: on a sphere, the sum of the angles in a triangle depends on the size of the triangle, so the directions from A to B and from B to A aren't as closely related as you would expect.

The Craig retroazimuthal projection was invented by James Ireland Craig in 1909. He used Mecca as his centre point to make a map that shows muslims across the world which direction they should face to pray.

The picture below shows what three spaceships travelling in a straight lines on a sphere looks like on this projection.

You can play Mathsteroids in Craig retroazimuthal mode here to explore the projection yourself. This is perhaps the hardest of all to play, as (a) two different parts of the sphere overlap on the map, and (b) the map is actually infinitely tall, so quite a bit of it is off the edge of the visible game area.

The final projection I'd like to show you is the stereographic projection.

Imagine that a sphere is sitting on a 2D plane. Take a point on the sphere. Imagine a straight line through this point and the point at the top of the sphere. The point where this line meets the 2D plane is stereographic projection of the point on the sphere.

This projection (backwards) can be used to represent the every complex number as a point on a sphere: this is called the Riemann sphere.

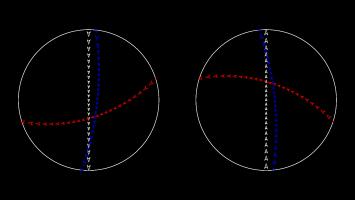
To make Mathseteroids playable after this projection, I split the sphere into 2 hemisphere and projected each seperately to give two circles. You can play Mathsteroids in stereographic projection mode here. Three spaceships travelling in straight lines on this projection are shown below.

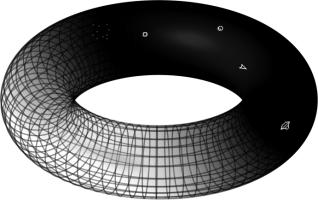
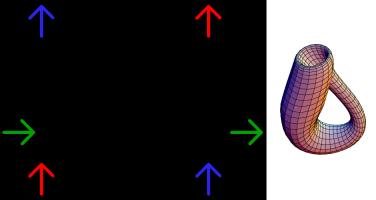
... and if you still don't like map projections, you can still enjoy playing Mathsteroids on an old fashioned torus. Or on a Klein bottle or the real projective plane. Don't forget to take a short break from playing to head over to The Aperiodical and vote (voting now closed).

Two years ago, I built a copy of MENACE (Machine Educable Noughts And Crosses Engine). Since then, it's been to many Royal Institution masterclasses, visted Manchester and met David Attenborough. When I'm not showing them off, the 304 matchboxes that make up my copy of MENACE live in this box:

This box isn't very big, which might lead you to wonder how big MENACE-style machines would be for other games.

In A matchbox game learning-machine by Martin Gardner [1], the game of Hexapawn was introduced. Hexapawn is played on a 3×3 grid, and starts with three pawns facing three pawns.

The pieces move like pawns: they may be either moved one square forwards into an empty square, or take another pawn diagonally (the pawns are not allowed to move forwards two spaces on their first move, as they can in chess). You win if one of your pawns reaches the other end of the board. You lose if none of your pieces can move.

The game was invented by Martin Gardner as a good game for his readers to build a MENACE-like machine to play against, as there are only 19 positions that can face player two, so only 19 matchboxes are needed to make HER (Hexapawn Educable Robot). (HER plays as player two, as if player two plays well they can always win.)

In Nine Men's Morris, two players first take turns to place pieces on the board, before taking turns to move pieces to adjacent spaces. If three pieces are placed in a row, a player may remove one of the opponent's pieces. It's a bit like Noughts and Crosses, but with a bit more chance of it not ending in a draw.

In Solving Nine Men's Morris by Ralph Gasser [2], the number of possible game states in Nine Men's Morris is given as approximately \(10^{10}\). To build MEME (Machine Educable Morris Engine), you would need this many matchboxes. These boxes would form a sphere with radius 41m: that's approximately the length of two tennis courts.

As a nice bonus, if you build MEME, you'll also smash the world record for the largest matchbox collection.

In Symbolic classification of general two-player games by Stefan Edelkamp and Peter Kissmann [3], the number of possible game states in Connect 4 is given as 4,531,985,219,092. The boxes used to make COFFIN (COnnect Four Fighting INstrument) would make a sphere with radius 302m: approximately the height of the Eiffel Tower.

In Solving the game of Checkers by Jonathan Schaeffer and Robert Lake [4], the number of possible game states in Draughts is given as approximately \(5\times10^{20}\). The boxes needed to build DOCILE (Draughts Or Checkers Intelligent Learning Engine) would make a sphere with radius 151km.

If the centre of DOCILE was in London, some of the boxes would be in Sheffield.

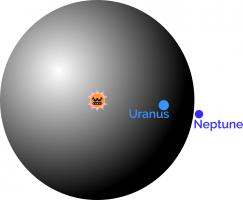
The number of possible board positions in chess is estimated to be around \(10^{43}\). The matchboxes needed to make up CLAWS (Chess Learning And Winning System) would fill a sphere with radius \(4\times10^{12}\)m.

If the Sun was at the centre of CLAWS, you might have to travel past Uranus on your search for the right box.

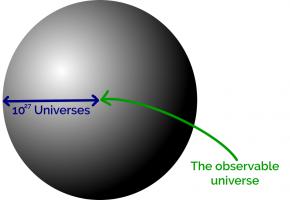
The number of possible positions in Go is estimated to be somewhere near \(10^{170}\). To build MEGA (Machine Educable Go Appliance), you're going to need enough matchboxes to make a sphere with radius \(8\times10^{54}\)m.

The observable universe takes up a tiny space at the centre of this sphere. In fact you could fit around \(10^{27}\) copies of the universe side by side along the radius of this sphere.

It's going to take you a long time to look through all those matchboxes to find the right one...

In 1969, Sid Sackson published his magnum opus: A Gamut of Games, a collection of 38 games that can all be played with pen and paper or a pack of cards.

One of the best games I've tried so far from the book is James Dunnigan's Origins of World War I. The original version from the book gets you to start by drawing a large table to play on, and during play requires a fair bit of flicking backwards and forwards to check the rules. To make playing easier, I made this handy pdf that contains all the information you need to play the game.

Origins of World War I is a game for five players (although it can be played with 3 or 4 people; details at the end). To play you will need a printed copy of the pdf, a pen or pencil, and a 6-sided dice.

Each player picks one of the five nations along the top of the board: Britain, France, Germany, Russia, or Austria–Hungary. Once you've picked your countries, you are ready to begin.

The countries take turns in the order Britain, France, Germany, Russia, or Austria–Hungary: the same order the countries are written across the top and down the side of the board. A player's turn involves two things: (1) adding "political factors"; (2) carrying out a "diplomatic attack".

First the player adds political factors (PFs). On their turn, Britain adds 14 PFs, France adds 12 PFs, Germany adds 16 PFs, Russia adds 10 PFs, and Austria–Hungary adds 10 PFs. These numbers are shown under the names of the countries on the left hand side of the board. A player can add at most 5 PFs to each country per turn, although they may add as many PFs as they like to their own country. The number of PFs a player adds to each country should be written in the boxes in the players column.

For example, Britain may choose to add 5 PFs in Italy, 2 in the Far East and 12 in Britain. This would be added to the board by writing the relevant numbers in the Italy, Far East and Britain rows of the Britain column.

After adding PFs, a player may choose to carry out a diplomatic attack. If so the player chooses one of the other four players to attack, and a country in which this attack takes place. Both players must have some PFs in the country where the attack takes place. The dice is rolled. The outcome of the attack depends on how much the attacker outnumbers the defender and the value rolled: these are shown to the right of the board. The three possible outcomes are: Attacker Eliminated (AE), which causes the attacker's PFs in this country to be reduced to 0; Exchange (EX), which causes both players' PFs in this country to be reduced by the same amount so that one player is left with 0; and Defender Eliminated (DE), wich causes the defender's PFs in this country to be reduced to 0.

For example, Britain may choose to attack Germany in Africa. If Britain and Germany have 10 and 4 PFs in Africa (respectively), then Britain outnumbers Germany 2 to 1. The dice is rolled. If a 1 is rolled, the attacker (Britain) is eliminated, leaving Britain on 0 and Germany on 4. If one of 2-5 is rolled, the players exchange, leaving Britain on 6 and Germany on 0. If a 6 is rolled, the defender (Germany) is eliminated, leaving Britain on 10 and Germany on 0.

The game ends after each play has played 10 turns. The number of turns may be kept track of by crossing out a number in the Turn Counter to the right of the board after each round of 5 turns.

If a player has 10 or more PFs in a country, then they have Treaty Rights (TR) with that country. Each player scores point by achieving TR with other countries. TR are not symmetric: if Russia has TR with Germany, then this does not mean that Germany automatically has TR with Russia.

The number of points scored by a player for obtaining TR with other countries are printed in the boxes on the board. The numbers in brackets are only scored if the TR are exclusive: ie if no other country also has TR with that country. Additionally, points are awarded to Britain, France and Germany if the objectives in the boxes at the foot of their columns are satisfied.

For example, Britain scores 3 points if they have TR with Italy, 1 point if they have TR with Greece, 2 points if they have TR with Turkey. and 4 points if they have exclusive TR with the Far East. Britain also scores 10 points if no other nation has more than 12 points.

During the game, players are encouraged to make deals with other players: for example, Britain may agree to not add PFs in Serbia if Russia agrees to carry diplomatic attacks against Germany in Bulgaria. Deals can of course be broken by either player later in the game.

Two players may also enter into a more formal alliance, leading to their two nations working together for the rest of the game. These alliances may not be broken. If two players are allied, then at the end of the game, their scores are added: if this total is higher than the scores of the other three players combined, then the allies win; if not, then the highest score among the other three wins.

During a game, it is possible for two different alliances to form (these must be between two different pairs of nations: a country cannot form two alliances, and three countries cannot form a three-way alliance). In this case, a pair of allies wins if their combined score is larger than the combined score of the other three players. If neither pair of allies scores this high, the unallied player wins.

Alliances can be used to play Origins of World War I with fewer than 5 players. To play with four players, an alliance can be formed at the start of the game, with one player playing both nations in the alliance. To play with three players, the game can be started with two alliances already in place.

If you've ready this far, then you're now fully prepared to play Origins of World War I, so print the pdf, invite 4 friends over, and have a game...

A few weeks ago, I took the copy of MENACE that I built to Manchester Science Festival, where it played around 300 games against the public while learning to play Noughts and Crosses. The group of us operating MENACE for the weekend included Matt Parker, who made two videos about it. Special thanks go to Matt, plus Katie Steckles, Alison Clarke, Andrew Taylor, Ashley Frankland, David Williams, Paul Taylor, Sam Headleand, Trent Burton, and Zoe Griffiths for helping to operate MENACE for the weekend.

As my original post about MENACE explains in more detail, MENACE is a machine built from 304 matchboxes that learns to play Noughts and Crosses. Each box displays a possible position that the machine can face and contains coloured beads that correspond to the moves it could make. At the end of each game, beads are added or removed depending on the outcome to teach MENACE to play better.

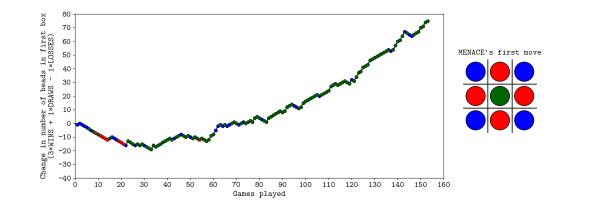
On Saturday, MENACE was set up with 8 beads of each colour in the first move box; 3 of each colour in the second move boxes; 2 of each colour in third move boxes; and 1 of each colour in the fourth move boxes. I had only included one copy of moves that are the same due to symmetry.

The plot below shows the number of beads in MENACE's first box as the day progressed.

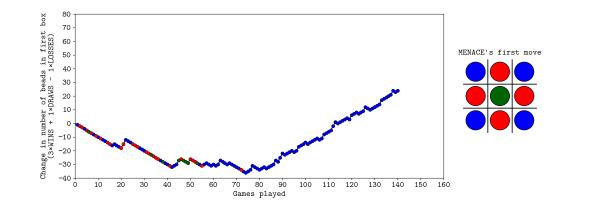
Originally, we were planning to let MENACE learn over the course of both days, but it learned more quickly than we had expected on Saturday, so we reset is on Sunday, but set it up slightly differently. On Sunday, MENACE was set up with 4 beads of each colour in the first move box; 3 of each colour in the second move boxes; 2 of each colour in third move boxes; and 1 of each colour in the fourth move boxes. This time, we left all the beads in the boxes and didn't remove any due to symmetry.

The plot below shows the number of beads in MENACE's first box as the day progressed.

You can download the full set of data that we collected over the weekend here. This includes the first two moves and outcomes of all the games over the two days, plus the number of beads in each box at the end of each day. If you do something interesting (or non-interesting) with the data, let me know!

In many early arcade games, the size of the playable area was limited by the size of the screen. To make this area seem larger, or to make gameplay more interesting, many games used wraparound; allowing the player to leave one side of the screen and return on another. In Pac-Man, for example, the player could leave the left of the screen along the arrow shown and return on the right, or vice versa.

Pac-Man's apparent teleportation from one side of the screen to the other may seem like magic, but it is more easily explained by the shape of Pac-Man's world being a cylinder.

Rather than jumping or teleporting from one side to the other, Pac-Man simply travels round the cylinder.

Bubble Bobble was first released in 1986 and features two dragons, Bub and Bob, who are tasked with rescuing their girlfriends by trapping 100 levels worth of monsters inside bubbles. In these levels, the dragons and monsters may leave the bottom of the screen to return at the top. Just like in Pac-Man, Bub and Bob live on the surface of a cylinder, but this time it's horizontal not vertical.

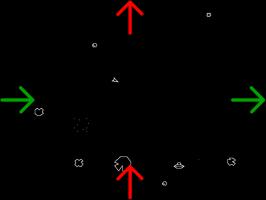
A very large number of arcade games use left-right or top-bottom wrapping and have the same cylindrical shape as Pac-Man or Bubble Bobble. In Asteroids, both left-right and top-bottom wrapping are used.

The ships and asteroids in Asteroids live on the surface of a torus, or doughnut: a cylinder around to make its two ends meet up.

There is, however, a problem with the torus show here. In Asteroids, the ship will take amount of time to get from the left of the screen to the right however high or low on the screen it is. But the ship can get around the inside of the torus shown faster than it can around the outside, as the inside is shorter. This is because the screen of play is completely flat, while the inside and outside halves of the torus are curved.

It is impossible to make a flat torus in three-dimensional space, but it is possible to make one in four-dimensional space. Therefore, while Asteroids seems to be a simple two-dimensional game, it is actually taking place on a four-dimensional surface.

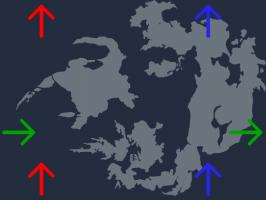
Wrapping doesn't only appear in arcade games. Many games in the excellent Final Fantasy series use wrapping on the world maps, as shown here on the Final Fantasy VIII map.

Just like in Asteroids, this wrapping means that Squall & co. carry out their adventure on the surface of a four-dimensional flat torus. The game designers, however, seem to not have realised this, as shown in this screenshot including a spherical (!) map.

Due to the curvature of a sphere, lines that start off parallel eventually meet. This makes it impossible to map nicely between a flat surface to a sphere (this is why so many different map projections exist), and heavily complicates the task of making a game with a truly spherical map. So I'll let the Final Fantasy VIII game designers off. Especially since the rest of the game is such incredible fun.

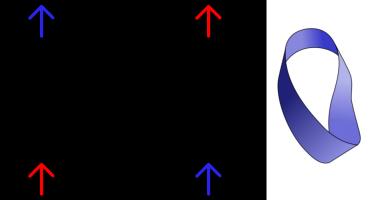
It is sad, however, that there are no games (at leat that I know of) that make use of the great variety of different wrapping rules available. By only slightly adjusting the wrapping rules used in the games in this post, it is possible to make games on a variety of other surfaces, such a Klein bottles or Möbius strips as shown below.

If you know of any games make use of these surfaces, let me know in the comments below!