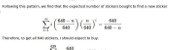Blog
2016-06-29
Since Electromagnetic Field 2014, I have been slowly making
progress on a recreational math problem about braiding. In this blog post, I
will show you the type of braid I am interested in and present the problem.
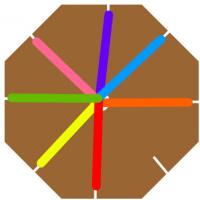
Making an (8,3) braid
To make what I will later refer to as an (8,3) braid, you will need:
- 7 lengths of coloured wool, approx 50cm each
- Cardboard
- Scissors
- A pencil
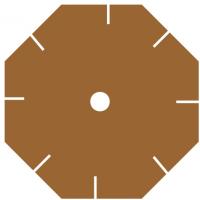
First, cut an octagon from the cardboard. The easiest way to do this is
to start with a rectangle, then cut its corners off.
Next, use the pencil to punch a hole in the middle of your octagon and
cut a small slit in each face of the octagon.
Now, tie the ends of your wool together, and put them through the hole.
pull each strand of wool into one of the slits.
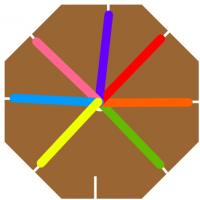
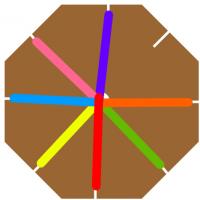
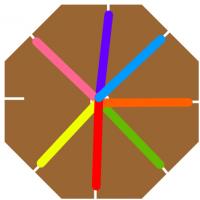
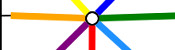
Now you are ready to make a braid. Starting from the empty slit, count around
to the third strand of will. Pull this out of its slit then into the empty slit.
Then repeat this starting at the newly empty slit each time. After a short time,
a braid should form through the hole in the cardboard.
I call the braid you have just made the (8,3) braid, as there are 8 slits and
you move the 3rd strand each time. After I first made on of these braid, I began
to wonder what was special about 8 and 3 to make this braid work, and for what
other numbers \(a\) and \(b\) the (\(a\),\(b\)) would work.
In my next blog post, I will give two conditions on \(a\) and \(b\) that cause
the braid to fail. Before you read that, I recommend having a go at the problem
yourself. To help you on your way, I am compiling a list of braids that are known
to work or fail at mscroggs.co.uk/braiding. Good luck!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2020-04-20
@no: yes, although rectangles work surprisingly wellMatthew
Add a Comment
2016-06-05
The Game of Life is a cellular automaton invented by John Conway in 1970,
and popularised by Martin Gardner.
In Life, cells on a square grid are either alive or dead. It begins
at generation 0 with some cells alive and some dead. The cells' aliveness in
the following generations are defined by the following rules:
- Any live cell with four or more live neighbours dies of overcrowding.
- Any live cell with one or fewer live neighbours dies of loneliness.
- Any dead cell with exactly three live neighbours comes to life.
Starting positions can be found which lead to all kinds of behaviour:
from making gliders
to generating prime numbers.
The following starting position is one of my favourites:
It looks boring enough, but in the next generation, it will look like this:
If you want to confirm that I'm not lying, I recommend the free Game of Life Software Golly.
Going backwards
You may be wondering how I designed the starting pattern above. A first, it looks like a difficult task: each cell can be dead or alive,
so I need to check every possible combination until I find one. The number of combinations will be \(2^\text{number of cells}\). This will
be a very large number.
There are simplifications that can be made, however. Each of the letters above (ignoring the gs) is in a 3×3 block, surrounded
by dead cells. Only the cells in the 5×5 block around this can affect the letter. These 5×5 blocks do no overlap, so can be
calculated seperately. I doesn't take too long to try all the possibilities for these 5×5 blocks. The gs were then made by starting with an o and trying adding cells below.
Can I make my name?
Yes, you can make your name.
I continued the search and found a 5×5 block for each letter. Simply Enter your name in the box below and
these will be combined to make a pattern leading to your name!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-05-04
Back in 2014, I calculated the expected cost of
filling Panini world cup sticker album. I found that you should expect to buy
4505 stickers, or 1285 if you order the last 100 from the Panini website (this
includes the last 100). This would cost £413.24 or £133.99
respectively.
Euro 16 is getting close, so it's sticker time again. For the Euro 16
album there are 680 stickers to collect, 40 more than 2014's 640 stickers.
Using the same calculation method as before,
to fill the Euro 16 album, you should expect to buy 4828
stickers (£442.72), or 1400 (£134.32) if you order the last 100.
This, however, does not tell the whole story. Anyone who has collected
stickers as a child or an adult will know that half the fun comes from
swapping your doubles with friends. Getting stickers this way is not
taken into account in the above numbers.
Simulating a sticker collection
Including swaps makes the situation more complicated: too complicated
to easily calculate the expected cost of a full album. Instead, a different
method is needed. The cost of filling an album can be estimated by
simulating the collection lots of times and taking the average of the cost of
filling the album in each simulation. With enough simulations, this estimate
will be very close the the expected cost.
To get an accurate estimation, simulations are run,
calculating the running average as they go, until the running averages after recent simulations
are close together. (In the examples, I look for the four most recent running averages to be within 0.01.)
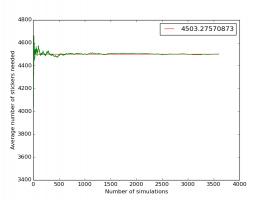
The plot below shows how the running average changes as more simulations are performed.
The simulations estimate the number of stickers needed as 4500. This is
very close to the 4505 I calculated last year.
Now that the simulations are set up, they can be used to see what happens if you have friends to swap with.
What should I do?
The plots below shows how the number of stickers you need to buy each changes based on how many friends you have.
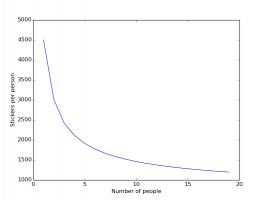
Stickers needed if you and your friends order no stickers.
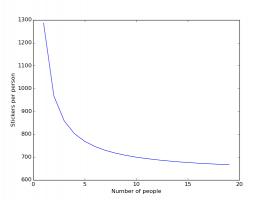
Stickers needed if you and your friends all order the last 100 stickers. The last 100 are not counted.
In both these cases, having friends reduces the number of stickers you need to buy significantly, with your first few friends
making the most difference.
Ordering the last 100 stickers looks to be a better idea than ordering no stickers. But how many stickers should you order to
minimise the cost? When you order stickers, you are guaranteed to get those that you need, but they cost more: ordered stickers cost 14p
each, while stickers in 6 pack multipacks come out at just 9.2p each. The next plot shows how the cost changes based on how many you order.
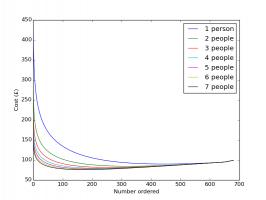
The expected cost of filling an album based on number of people in group and number of stickers ordered.
Each of the coloured curves represents a group of a different size. For each group, ordering no stickers works out the most
expensive—this is expected as so many stickers must be bought to find the last few stickers—and ordering all the stickers also works
out as not the best option. The best number to order
is somewhere in the middle, where the curve reaches its lowest point. The minimum points on each of these curves are summarised in the
next plots:
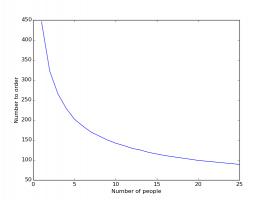
How the number you should order changes with the number of people in the group.
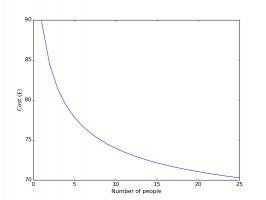
How the cost changes with the number of people in the group.
Again, having friends to swap with dramatically reduces the cost of filling an album. In fact, it will almost definitely pay off in future
swaps if you go out right now and buy starter packs for all your friends...
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-03-31
Pythagoras's Theorem is perhaps the most famous theorem in maths. It is also very old, and for over 2500 years mathematicians have been explaining why it is true.
This has led to hundreds of different proofs of the theorem. Many of them were collected in the 1920s in The pythagorean proposition by Elisha Scott Loomis [1]. Let's have a look at some of them.
Using similar triangles
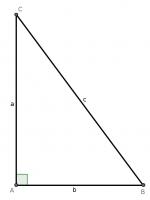
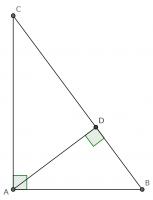
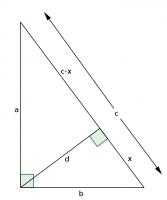
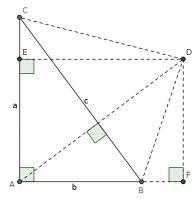
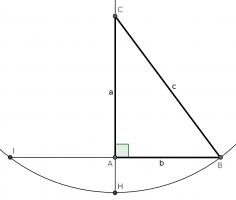
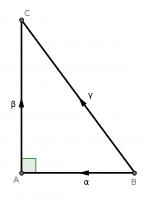
For our first proof, start with a right angled triangle, \(ABC\), with sides of lengths \(a\), \(b\) and \(c\).
Add a point \(D\) on the hypotenuse such that the line \(AD\) is perpendicular to \(BC\). Name the lengths as shown in the second diagram.
\(ABC\) and \(DBA\) are similar triangles, so:
$$\frac{b}{x}=\frac{c}{b}$$
$$b^2=xc$$
\(ABC\) and \(DAC\) are similar triangles, so:
$$\frac{a}{c-x}=\frac{c}{a}$$
$$a^2=c^2-cx$$
Adding the two equations gives:
$$a^2+b^2=c^2$$
Constructing a quadrilateral
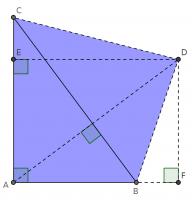
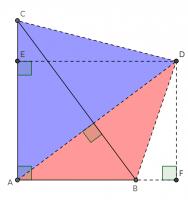
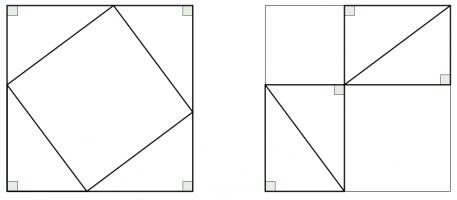
This proof shows the theorem is true by using extra lines and points added to the triangle. Start with \(ABC\) as before then add a point \(D\) such that \(AD\) and \(BC\) are perpendicular and of equal length. Add points \(E\) on \(AC\) and \(F\) on \(AB\) (extended) such that \(DE\) and \(AC\) are perpendicular and \(DF\) and \(AB\) are perpendicular.
By similar triangles, it can be seen that \(DF=b\) and \(DE=a\).
As the two diagonals of \(BACD\) are perpendicular, its area is \(\tfrac12c^2\).
The area of \(BACD\) is also equal to the sum of the areas of \(ABD\) and \(ACD\). The area of \(ABD\) is \(\tfrac12b^2\). The area of \(ACD\) is \(\tfrac12a^2\).
Therefore, \(\tfrac12a^2+\tfrac12b^2=\tfrac12c^2\), which implies that \(a^2+b^2=c^2\).
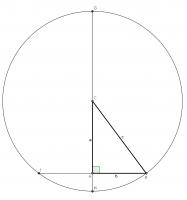
Using a circle
This proof again uses extra stuff: this time using a circle. Draw a circle of radius \(c\) centred at \(C\). Extend \(AC\) to \(G\) and \(H\) and extend \(AB\) to \(I\).
By the intersecting chord theorem, \(AH\times AG = AB\times AI\). Using the facts that \(AI=AB\) and \(CH\) and \(CG\) are radii, the following can be obtained from this:
$$(c-a)\times(c+a)=b\times b$$
$$c^2-a^2=b^2$$
$$a^2+b^2=c^2$$
Rearrangement proofs
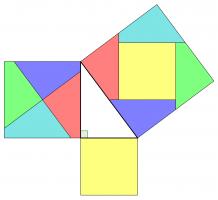
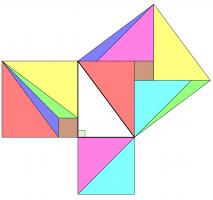
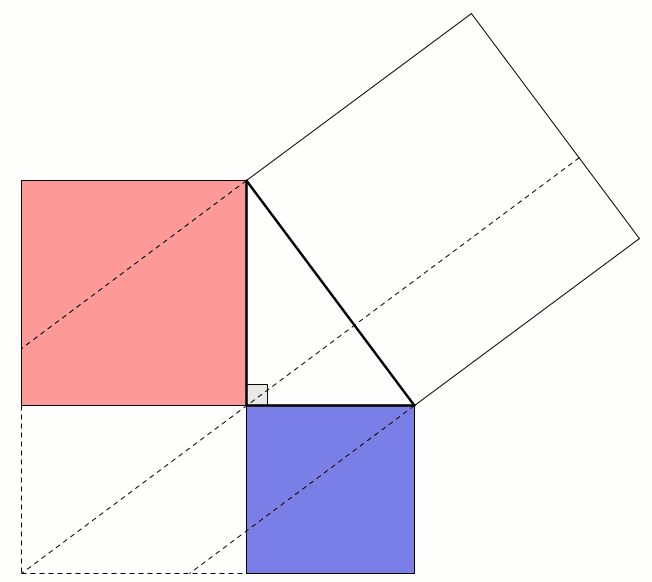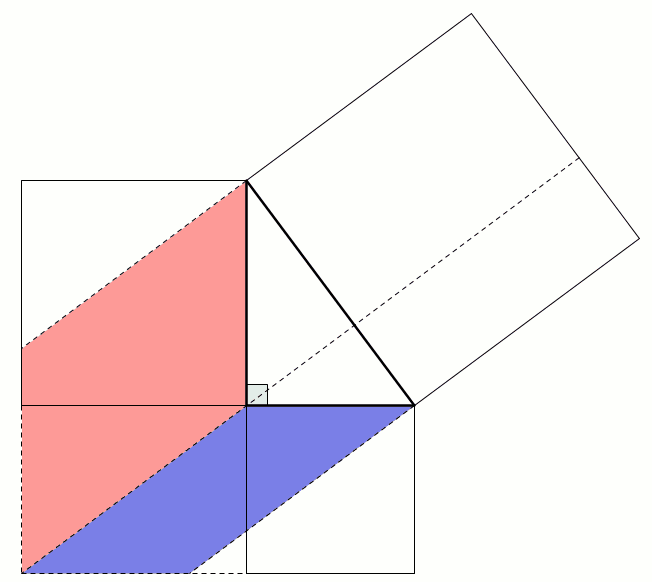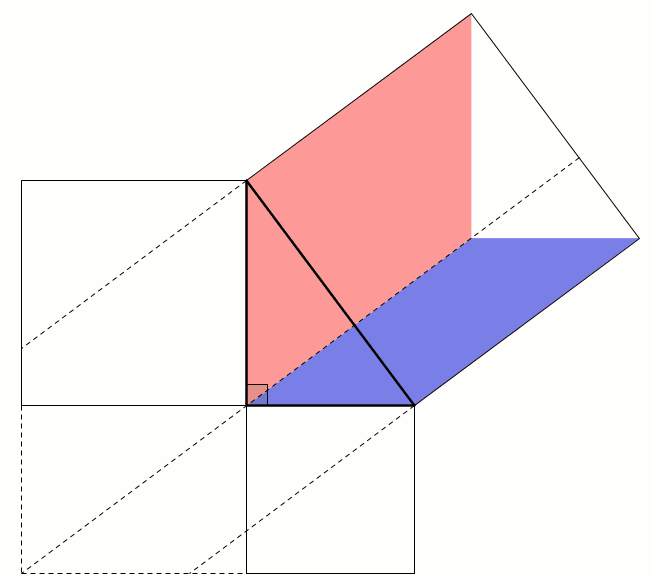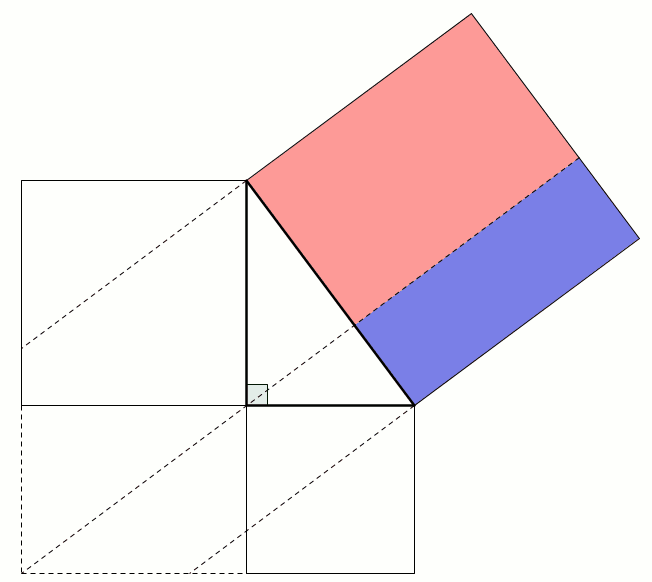
A popular method of proof is dissecting the smaller squares and rearranging the pieces to make the larger square. In both the following, the pieces are coloured to show which are the same:
Alternatively, the theorem could be proved by making copies of the triangle and moving them around. This proof was presented in The pythagorean proposition simply with the caption "LOOK":
This next proof uses the fact that two parallelograms with the same base and height have the same area: sliding the top side horizontally does not change the area. This allows us to move the smaller squares to fill the large square:
For this proof, start by labelling the sides of the triangle as vectors \(\alpha\), \(\beta\) and \(\gamma\).
Clearly, \(\gamma = \alpha+\beta\). Taking the dot product of each side with itself gives:
$$\gamma\cdot\gamma = \alpha\cdot\alpha+2\alpha\cdot\beta+\beta\cdot\beta$$
\(\alpha\) and \(\beta\) are perpendicular, so \(\alpha\cdot\beta=0\); and dotting a vector with itself gives the size of the vector squared, so:
$$|\gamma|^2=|\alpha|^2+|\beta|^2$$
If you don't like any of these proofs, there are of course many, many more. Why don't you tweet me your favourite.
References
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-03-30
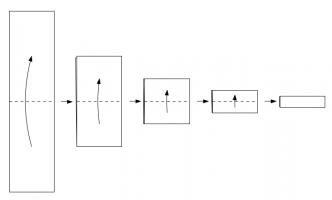
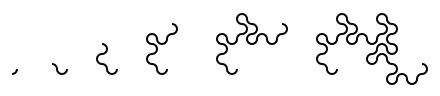
Take a piece of paper. Fold it in half in the same direction many times. Now unfold it. What pattern will the folds make?
I first found this question in one of Martin Gardner's books. At first, you might that the answer will be simple, but if you look at the shapes made for a few folds, you will see otherwise:
The curves formed are called dragon curves as they allegedly look like dragons with smoke rising from their nostrils. I'm not sure I see the resemblance:
As you increase the order of the curve (the number of times the paper was folded), the dragon curve squiggles across more of the plane, while never crossing itself. In fact, if the process was continued forever, an order infinity dragon curve would cover the whole plane, never crossing itself.
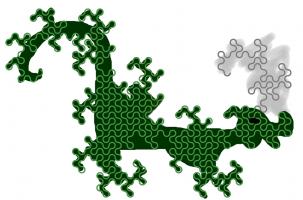
This is not the only way to cover a plane with dragon curves: the curves tessellate.

When tiled, this picture demonstrates how dragon curves tessellate. For a demonstration, try obtaining infinite lives...
Dragon curves of different orders can also fit together:
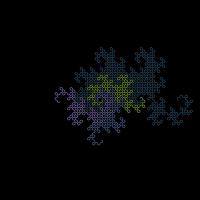
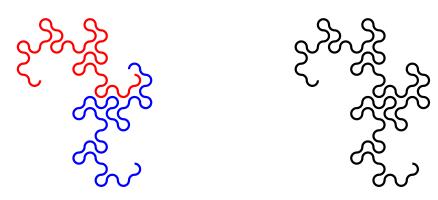
To generate digital dragon curves, first notice that an order \(n\) curve can be made from two order \(n-1\) curves:
This can easily be seen to be true if you consider folding paper: If you fold a strip of paper in half once, then \(n-1\) times, each half of the strip will have made an order \(n-1\) dragon curve. But the whole strip has been folded \(n\) times, so is an order \(n\) dragon curve.
Because of this, higher order dragons can be thought of as lots of lower order dragons tiled together. An the infinite dragon curve is actually equivalent to tiling the plane with a infinite number of dragons.
If you would like to create your own dragon curves, you can download the Python code I used to draw them from GitHub. If you are more of a thinker, then you might like to ponder what difference it would make if the folds used to make the dragon were in different directions.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment