Blog
2018-12-23
Recently, I made myself a new Christmas decoration:
Loyal readers may recognise the Platonic solid presents from last year's Christmas card, last year's
Advent calendar medals, or this year's Advent calendar medals.
If you'd like to make your own Platonic solids Christmas cross stitch, you can find the instructions below. I'm also currently putting together
some prototype Platonic solids cross stitch kits (that may be available to buy at some point in the future),
and will be adding these to the piles of prizes for this year's Advent calendar.
You will need
- A cross stitch needle
- Red cross stitch thread (for the ribbon)
- Black cross stitch thread (for the outlines)
- Non-red cross stitch thread (for the wrapping paper: I chose a different colour for each solid)
- Cross stitch aida
Instructions
Cross stitch thread is made up of 6 strands twisted together. When doing your cross stitch, it's best to use two strands at a time:
so start by cutting a sensible length of thread and splitting this into pairs of strands. Thread one pair of strands into the needle.
Following the patterns below, cross stitch rows of red and non-red crosses. To stitch a row, first go along the row sewing diagonals in one direction,
then go back along the row sewing the other diagonals. When you've finished the row, move the the row above and repeat. This is shown in the
animation below.
When doing the first row, make sure the stiches on the back cover the loose end of thread to hold it in place. Looking at the back of the
aida, it should look something like this:
When you are running out of thread, or you have finished a colour, finish a stitch so the needle is at the back.
Then pass the needle through some of the stitches on the back so that the loose end will be held in place.
The patterns for each solid are shown below. For each shape, the left pattern shows which colours you should cross in each square
(/ means red, o means non-red); and the right pattern shows where to add black lines after the crosses are all done.

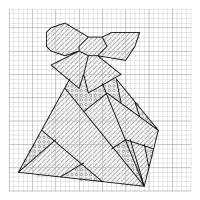
Pattern for a tetrahedron (click to enlarge)

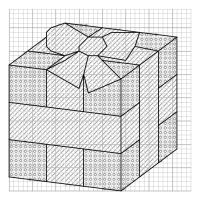
Pattern for a cube (click to enlarge)

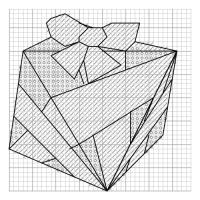
Pattern for a octahedron (click to enlarge)

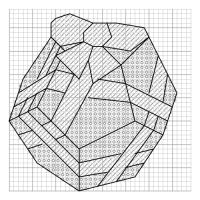
Pattern for a dodecahedron (click to enlarge)

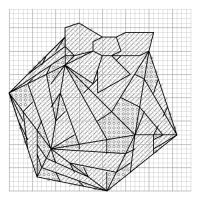
Pattern for a icosahedron (click to enlarge)
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-12-16
By now, you've probably noticed that I like teaching matchboxes to play noughts and crosses.
Thanks to comments on Hacker News, I discovered that I'm not the only one:
MENACE has appeared in, or inspired, a few works of fiction.
The Adolescence of P-1
The Adolescence of P-1 by Thomas J Ryan [1] is the story of Gregory Burgess, a computer programmer who writes a computer program that becomes sentient.
P-1, the program in question, then gets a bit murdery as it tries to prevent humans from deactivating it.
The first hint of MENACE in this book comes early on, in chapter 2, when Gregory's friend Mike says to him:
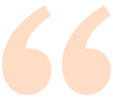
"Because I'm a veritable fount of information. From me you could learn such wonders as the gestation period of an elephant or how to teach a matchbox to win at tic-tac-toe."Taken from The Adolescence of P-1 by Thomas J Ryan [1], page 27

A few years later, in chapter 4, Gregory is talking to Mike again. Gregory asks:
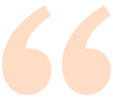
"... How do you teach a matchbox to play tic-tac toe?""What?""You heard me. I remember you once said you could teach a matchbox. How?""Jesus Christ! Let me think . . . Yeah . . . I remember now. That was an article in Scientific American quite a few years ago. It was a couple of years old when I mentioned it to you, I think.""How does it work?""Pretty good. Same principal of reward and punishment you use to teach a dog tricks, as I remember. Actually, you get several matchboxes. One for each possible move you might make in a game of tic-tac-toe. You label them appropriately, then you put an equal number of two different coloured beads in each box. The beads correspond to each yes/no decision you can make in a game. When a situation is reached, you grab the box for the move, shake it up, and grab a bead out of it. The bead indicates the move. You make a record of that box and color, and then make the opposing move yourself. You move against the boxes. If the boxes lose the game, you subtract a bead of the color you used from each of the boxes you used. If they win, you add a bead of the appropriate color to the boxes you used. The boxes lose quite a few games, theoretically, and after the bad moves start getting eliminated or statistically reduced to inoperative levels, they start to win. Then they never lose. Something like that. Check Scientific American about four years ago. How is this going to help you?"Taken from The Adolescence of P-1 by Thomas J Ryan [1], pages 41-42

The article in Scientific American that they're talking about is obviously A matchbox game learning-machine by Martin Gardner [2].
Mike, unfortunately, hasn't quite remembered perfectly how MENACE works: rather than having two colours in each box for yes and no, each box actually has a different colour for each possible move that could be made next.
But to be fair to Mike, he read the article around two years before this conversation so this error is forgivable.
In any case, this error didn't hold Gregory back, as he quickly proceeded to write a program, called P-1 inspired by MENACE.
P-1 was first intended to learn to connect to other computers through their phone connections and take control of their supervisor, but then
Gregory failed to close the code and it spent a few years learning everything it could before contacting Gregory, who was obviously a little
surprised to hear from it.
P-1 has also learnt to fear, and is scared of being deactiviated. With Gregory's help, P-1 moves much of itself to a more secure location.
Without telling Gregory, P-1 also attempts to get control of America's nuclear weapons to obtain its own nuclear deterrent, and starts
using its control over computer systems across America to kill anyone that threatens it.
Apart from a few Literary Review Bad Sex in Fiction Award worthy segments,
The Adolescence of P-1 is an enjoyable read.
Hide and Seek (1984)
In 1984, The Adolescence of P-1 was made into a Canadian TV film called Hide and Seek [3].
It doesn't seem to have made it to DVD, but luckily the whole film is on
YouTube.
About 24 minutes into the film, Gregory explains to Jessica how he made P-1:
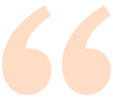
Gregory: First you end up with random patterns like this. Now there are certain rules: if a cell has one or two neighbours, it reproduces into the next generation. If it has no neighbours, it dies of loneliness. More than two it dies of overcrowding. Press the return key.Jessica: Okay. [pause] And this is how you created P-1?Gregory: Well, basically. I started to change the rules and then I noticed that the patterns looked like computer instructions. So I entered them as a program and it worked.Hide and Seek [3] (1984)

This is a description of a cellular automaton similar to Game of Life, and not a great way to make a machine that learns.
I guess the film's writers have worse memories than Gregory's friend Mike.
In fact, apart from the character names and the murderous machine, the plots of The Adolescence of P-1 and Hide and Seek don't have much in common.
Hide and Seek does, however, have a lot of plot elements in common with WarGames [4].
WarGames (1983)
In 1983, the film WarGames was released. It is the story of David, a hacker that tries to hack into a video game company's computer, but accidentally
hacks into the US governments computer and starts a game of Global thermonuclear war. At least David thinks it's a game, but actually
the computer has other ideas, and does everything in its power to actually start a nuclear war.
During David's quests to find out more about the computer and prevent nuclear war, he learns about its creator, Stephen Falken.
He describes him to his girlfriend, Jennifer:
David: He was into games as well as computers. He designed them so that they could play checkers or poker. Chess.Jennifer: What's so great about that? Everybody's doing that now.David: Oh, no, no. What he did was great! He designed his computer so it could learn from its own mistakes. So they'd be better they next time they played. The system actually learned how to learn. It could teach itself.WarGames [4] (1983)

Although David doesn't explain how the computer learns, he at least states that it does learn, which is more than Gregory managed in Hide and Seek.
David's research into Stephen Falken included finding an article called Falken's maze: Teaching a machine to learn in
June 1963's issue of Scientific American. This article and Stephen Falken are fictional, but perhaps its appearance in Scientific American
is a subtle nod to Martin Gardner and A matchbox game learning-machine.
WarGames was a successful film: it was generally liked by viewers and nominated for three Academy Awards. It seems likely that the creators of
Hide and Seek were really trying to make their own version of WarGames, rather than an accurate apatation of The Adolescence of P-1. This perhaps explains the similarities
between the plots of the two films.
Without a Thought
Without a Thought by Fred Saberhagen [5] is a short story published in 1963. It appears in a collection of related short stories by Fred Saberhagen called Bezerker.
In the story, Del and his aiyan (a pet a bit like a more intelligent dog; imagine a cross between R2-D2 and Timber) called Newton are in a spaceship fighting against a bezerker. The bezerker has
a mind weapon that pauses all intelligent thought, both human and machine. The weapon has no effect
on Newton as Newton's thought is non-intelligent.
The bezerker challenges Del to a simplified checker game, and says that if Del can play the game while the mind weapon is active, then he
will stop fighting.
After winning the battle, Del explains to his commander how he did it:
But the Commander was watching Del: "You got Newt to play by the following diagrams, I see that. But how could he learn the game?"Del grinned. "He couldn't, but his toys could. Now wait before you slug me" He called the aiyan to him and took a small box from the animal's hand. The box rattled faintly as he held it up. On the cover was pasted a diagram of on possible position in the simplified checker game, with a different-coloured arrow indicating each possible move of Del's pieces.It took a couple of hundred of these boxes," said Del. "This one was in the group that Newt examined for the fourth move. When he found a box with a diagram matching the position on the board, he picked the box up, pulled out one of these beads from inside, without looking – that was the hardest part to teach him in a hurry, by the way," said Del, demonstrating. "Ah, this one's blue. That means, make the move indicated on the cover by the blue arrow. Now the orange arrow leads to a poor position, see?" Del shook all the beads out of the box into his hand. "No orange beads left; there were six of each colour when we started. But every time Newton drew a bead, he had orders to leave it out of the box until the game was over. Then, if the scoreboard indicated a loss for our side, he went back and threw away all the beads he had used. All the bad moves were gradually eliminated. In a few hours, Newt and his boxes learned to play the game perfectly."Taken from Without a Thought by Fred Saberhagen [5]

It's a good thing the checkers game was simplified, as otherwise the number of boxes needed to play would be
way too big.
Overall, Without a Thought is a good short story containing an actually correctly explained machine learning algorithm. Good job Fred Saberhagen!
References
[1] The Adolescence of P-1 by Thomas J Ryan. 1977.
[4] WarGames. 1993.
[5] Without a Thought by Fred Saberhagen. 1963.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-12-08
Just like last year and the year before, TD and I spent some time in November this year designing a Chalkdust puzzle Christmas card.
The card looks boring at first glance, but contains 10 puzzles. By splitting the answers into pairs of digits, then drawing lines between the dots on the cover for each pair of digits (eg if an answer is 201304, draw a line from dot 20 to dot 13 and another line from dot 13 to dot 4), you will reveal a Christmas themed picture. Colouring the region of the card labelled R red or orange will make this picture even nicer.
If you want to try the card yourself, you can download this pdf. Alternatively, you can find the puzzles below and type the answers in the boxes. The answers will be automatically be split into pairs of digits, lines will be drawn between the pairs, and the red region will be coloured...
If you enjoy these puzzles, then you'll almost certainly enjoy this year's puzzle Advent calendar.
| 1. | What is the smallest four digit number whose digits add up to 6? | Answer |
| 2. | What is the length of the hypotenuse of a right angled triangle whose two shorter sides have lengths 152,560 and 114,420? | Answer |
| 3. | What is the lowest common multiple of 1346 and 196? | Answer |
| 4. | What is the sum of all the odd numbers between 0 and 698? | Answer |
| 5. | How many numbers are there between 100 and 10,000 that contain no 0, 1, 2, or 3? | Answer |
| 6. | How many factors (including 1 and the number itself) does the number \(2^{13}\times3^{19}\times5^9\times7^{39}\) have? | Answer |
| 7. | In a book with pages numbered from 1 to 16,020,308, what do the two page numbers on the centre spread add up to? | Answer |
| 8. | You think of a number, then make a second number by removing one of its digits. The sum of these two numbers is 18,745,225. What was your first number? | Answer |
| 9. | What is the largest number that cannot be written as \(13a+119b\), where \(a\) and \(b\) are positive integers or 0? | Answer |
| 10. | You start at the point (0,0) and are allowed to move one unit up or one unit right. How many different paths can you take to get to the point (7,6)? | Answer |
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
@Carmel: It's not meant to check your answers. It only shows up red if the number you enter cannot be split into valid pairs (eg the number has an odd number of digits or one of the pairs of digits is greater than 20).
Matthew
Great puzzle problems! Hint on #9: try starting with an analogous problem using smaller numbers (e.g. 3a + 10b). This helped me to see what I had to do more generally.
Noah
Add a Comment
2018-11-25
This year, the front page of mscroggs.co.uk will once again feature an advent calendar, just like last year, the year before and the year before. Behind each door, there will be a puzzle with a three digit solution. The solution to each day's puzzle forms part of a logic puzzle:
It's nearly Christmas and something terrible has happened: one of Santa's five helpers—Meg Reeny, Fred Metcalfe, Jo Ranger, Kip Urples, and Bob Luey—has stolen all the presents during the North Pole's annual Sevenstival. You need to find the culprit before Christmas is ruined for everyone.
Every year in late November, Santa is called away from the North Pole for a ten hour meeting in which a judgemental group of elders decide who has been good and who has been naughty. While Santa is away, it is traditional for his helpers celebrate Sevenstival.
Sevenstival gets its name from the requirement that every helper must take part in exactly seven activities during the celebration; this year's
available activities were billiards, curling, having lunch, solving maths puzzles, table tennis, skiing, chess, climbing and ice skating.
Each activity must be completed in one solid block: it is forbidden to spend some time doing an activity, take a break to do something else then return to the first activity.
This year's Sevenstival took place between 0:00 and 10:00 (North Pole standard time).
During this year's Sevenstival, one of Santa's helpers spent the time for one of their seven activities stealing all the presents from Santa's workshop.
Santa's helpers have 24 pieces of information to give to you, but the culprit is going to lie about everything in an attempt to confuse you, so be careful who you trust.
Behind each day (except Christmas Day), there is a puzzle with a three-digit answer.
Each of these answers forms part of a fact that one of the helpers tells you.
You must work out who the culprit is and between which times the theft took place.
Ten randomly selected people who solve all the puzzles and submit their answers to the logic puzzle using the form behind the door on the 25th will win prizes!
The winners will also receive one of these medals:
As you solve the puzzles, your answers will be stored. To share your stored answers between multiple devices, enter your email address below the calendar and you will be emailed a magic link to visit on your other devices.
Behind the door on Christmas Day, there will be a form allowing you to submit your answers. The winner will be randomly chosen from all those who submit the correct answer before the end of 2018. Each day's puzzle (and the entry form on Christmas Day) will be available from 5:00am GMT. But as the winners will be selected randomly, there's no need to get up at 5am on Christmas Day to enter!
To win a prize, you must submit your entry before the end of 2018. Only one entry will be accepted per person. If you have any questions, ask them in the comments below or on Twitter.
So once December is here, get solving! Good luck and have a very merry Christmas!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2018-09-13
This is a post I wrote for round 2 of The Aperiodical's Big Internet Math-Off 2018. As I went out in round 1 of the Big Math-Off, you got to read about the real projective plane instead of this.
Polynomials are very nice functions: they're easy to integrate and differentiate, it's quick to calculate their value at points, and they're generally friendly to deal with. Because of this, it can often be useful to find a polynomial that closely approximates a more complicated function.
Imagine a function defined for \(x\) between -1 and 1. Pick \(n-1\) points that lie on the function. There is a unique degree \(n\) polynomial (a polynomial whose highest power of \(x\) is \(x^n\)) that passes through these points. This polynomial is called an interpolating polynomial, and it sounds like it ought to be a pretty good approximation of the function.
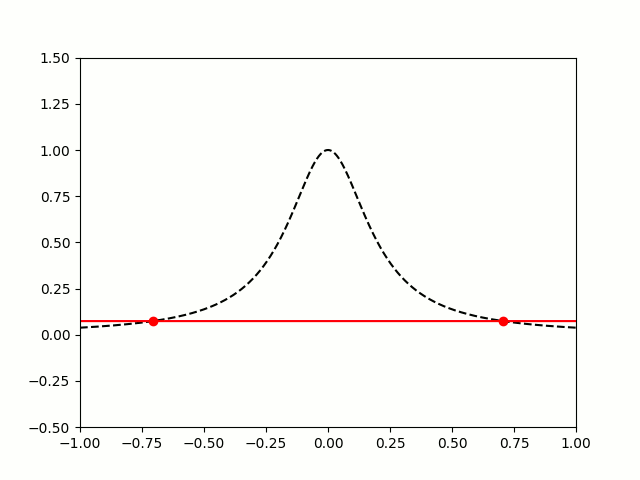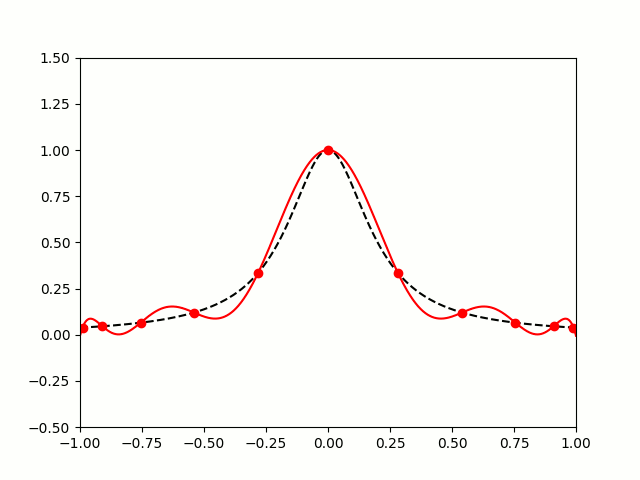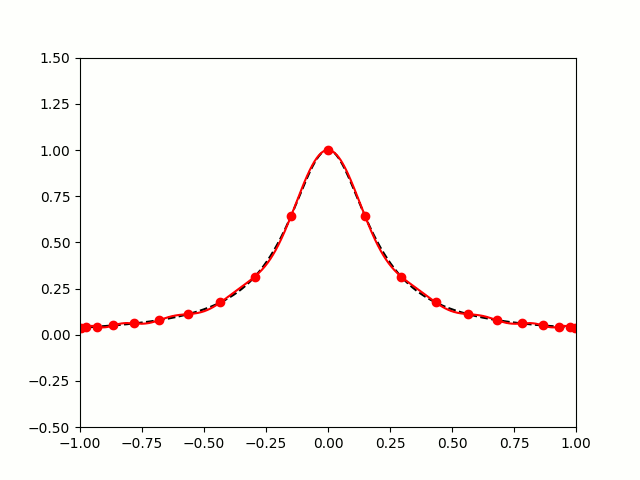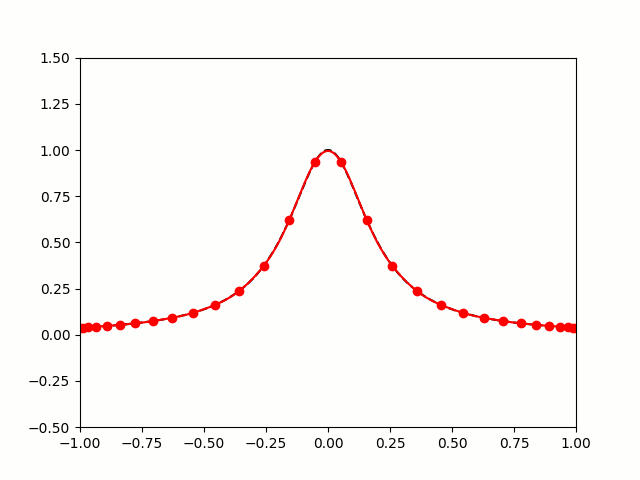
So let's try taking points on a function at equally spaced values of \(x\), and try to approximate the function:
$$f(x)=\frac1{1+25x^2}$$
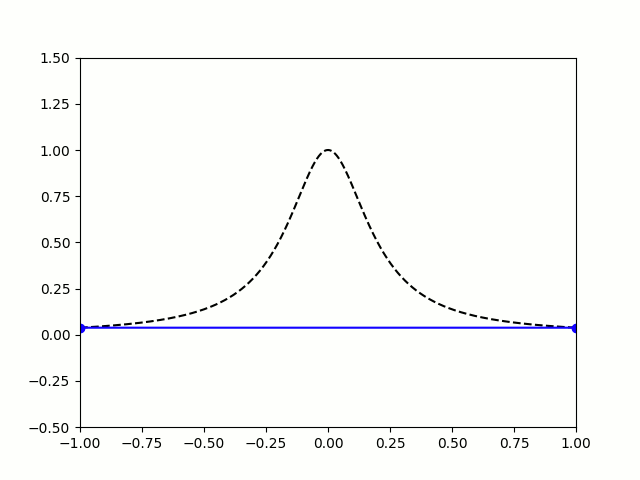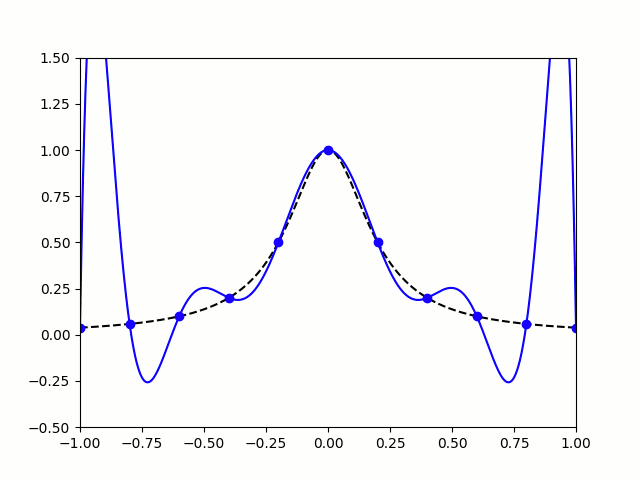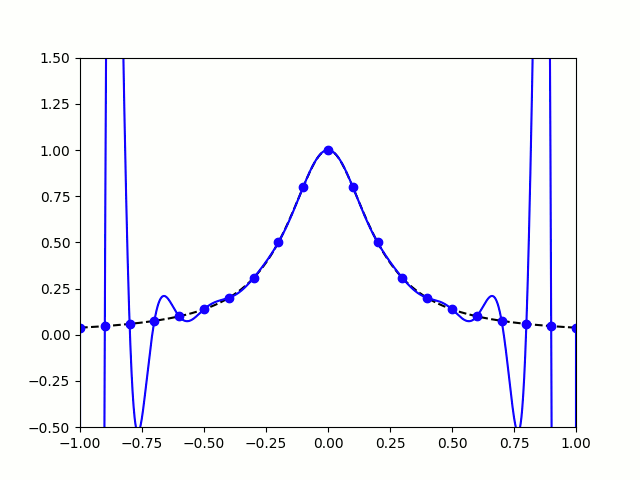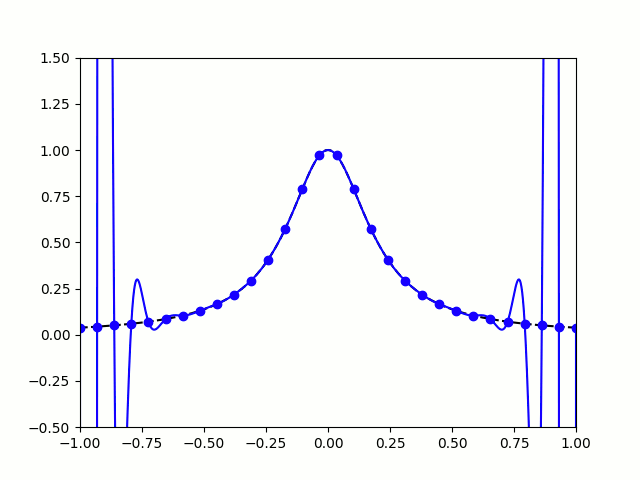
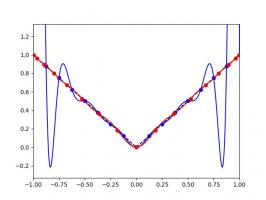
I'm sure you'll agree that these approximations are pretty terrible, and they get worse as more points are added. The high error towards 1 and -1 is called Runge's phenomenon, and was discovered in 1901 by Carl David Tolmé Runge.
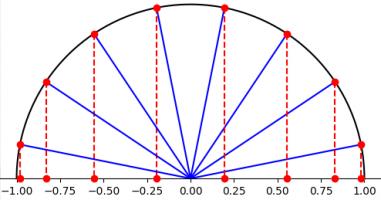
All hope of finding a good polynomial approximation is not lost, however: by choosing the points more carefully, it's possible to avoid Runge's phenomenon. Chebyshev points (named after Pafnuty Chebyshev) are defined by taking the \(x\) co-ordinate of equally spaced points on a circle.
The following GIF shows interpolating polynomials of the same function as before using Chebyshev points.
Nice, we've found a polynomial that closely approximates the function... But I guess you're now wondering how well the Chebyshev interpolation will approximate other functions. To find out, let's try it out on the votes over time of my first round Big Internet Math-Off match.
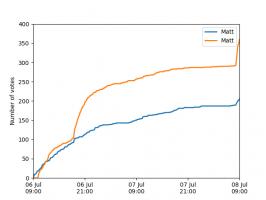
The graphs below show the results of the match over time interpolated using 16 uniform points (left) and 16 Chebyshev points (right). You can see that the uniform interpolation is all over the place, but the Chebyshev interpolation is very close the the actual results.
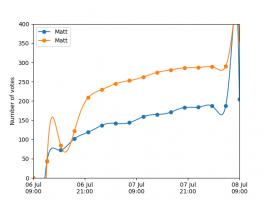
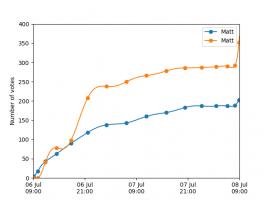
Scroggs vs Parker, 6-8 July 2018, approximated using uniform points (left) and Chebyshev points (right)
But maybe you still want to see how good Chebyshev interpolation is for a function of your choice... To help you find out, I've wrote @RungeBot, a Twitter bot that can compare interpolations with equispaced and Chebyshev points.
Since first publishing this post, Twitter's API changes broke @RungeBot, but it lives on on Mathstodon: @RungeBot@mathstodon.xyz.
Just tweet it a function, and it'll show you how bad Runge's phenomenon is for that function, and how much better Chebysheb points are.
For example, if you were to toot "@RungeBot@mathstodon.xyz f(x)=abs(x)", then RungeBot would reply: "Here's your function interpolated using 17 equally spaced points (blue) and 17 Chebyshev points (red). For your function, Runge's phenomenon is terrible."
A list of constants and functions that RungeBot understands can be found here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Hi Matthew, I really like your post. Is there a benefit of using chebyshev spaced polynomial interpolation rather than OLS polynomial regression when it comes to real world data? It is clear to me, that if you have a symmetric function your approach is superior in capturing the center data point. But in my understanding in your vote-example a regression minimizing the residuals would be preferrable in minimizing the error. Or do I miss something?
Benedikt
Add a Comment