Hide answer & extension
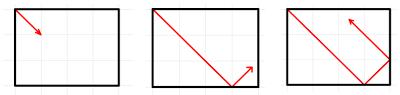
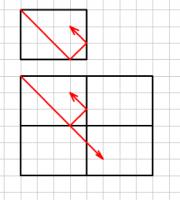
If mirrors were placed along the walls of the rectangle, the ball would appear to travel in a straight line across a grid of rectangles:
Viewed this way, the ball will still stop once it reaches a corner:
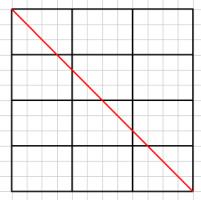
For an \(n\) by \(m\) (in above example: \(n=4\), \(m=3\)) rectangle, this will occur once the ball has travelled through \(\mathrm{lcm}(n,m)\) squares.
$$\mathrm{Let\ }a=\frac{\mathrm{lcm}(n,m)}{n}$$
$$\mathrm{Let\ }b=\frac{\mathrm{lcm}(n,m)}{m}$$
On its way to the corner, the ball will bounce \(b-1\) times off the top and bottom and \(a-1\) times off the sides. It can be seen that if \(a-1\) is even, then the ball will end in one of the corners on the right hand side. The complete results can be seen in the following
Carroll diagram:
| \(a-1\) odd | \(a-1\) even |
| \(b-1\) odd | Top left | Top right |
| \(b-1\) even | Bottom left | Bottom right |
It can be shown that the ball will never finish in the top left (where it started) as this would require it to travel through the bottom right first. Therefore the following holds:
| \(a\) even | \(a\) odd |
| \(b\) even | | Top right |
| \(b\) odd | Bottom left | Bottom right |
Extension
For which sizes of rectangle will the path of the ball make the same pattern?
![](javascript:showlimage("trim-bb.png"))
![](javascript:showlimage("bb-soln1.png"))
![](javascript:showlimage("bb-soln2.png"))