Blog
2014-06-21
With World Cup fever taking over, you may have forgotten that Wimbledon is just a few days away.
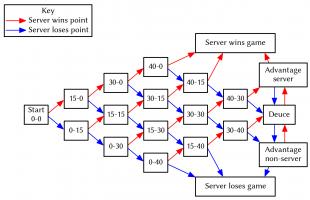
Tennis scoring
Tennis matches are split into sets (three sets for ladies' matches, five sets for men's), which are in turn split into games. The players take it in turns to serve for a game. The scoring in a game is probably best explained with a flowchart (click to enlarge):
To win a set, a player must win at least six games and two more games than their opponent. If the score reaches six games all, then a tie break is played. In this tie break, the first player to win at least seven points and two points more than their opponent wins. In the final set there is no tie break, so matches can last a long time.
Winning with the smallest share of points
Due to the way tennis is split into sets and games, the player who wins the most points will not necessarily win the match. This got me thinking: what is the smallest proportion of points which can be won while still winning the tennis match?
First, let's consider a men's match. In order to win with the lowest proportion of points, our player should let his opponent win two sets without winning a point and win the other three sets. In the two lost sets, the opponent should win 0-6 taking every point: in total the opponent will win 48 points in these sets.
Leaving the final set for now, the other two sets are won by our player. To win these with the smallest proportion of the points, they should be won 7-6 on a tie break. In the 6 lost games, the opponent should take all the points. In the won games and the tie break, our player should win by two points with the lowest total score. (Winning with more than the lowest total score will mean both players win an equal number of extra points, moving the proportion of points our player wins closer to 50%, higher than it needs to be.)
Therefore, our player will win 4 points out of 6 in the games he wins, win 0 out of 4 points in the games he loses and wins the tie break 7 points to 5. This means that in total our player will 62 points out of 144 in the two won sets.
For the same reason as above, the final set should be won with the lowest total score: 6-4. Using the same scores for each game, our player wins 24 points out of 52.
Overall, our player has won 86 points out of 244, a mere 35% of the points.
If the match is a ladies' match then the same analysis will work, but with each player winning one less set. This gives our player 55 points out of 148, 37% of the points.
This result demonstrates why tennis remains exciting through the whole match. The way tennis is split into sets and games means that our opponent can win 65% of the points but if the pressure gets to them at the most important points, our player can still win the match. This makes for a far more interesting competition than a simple race to one hundred points which could quickly become a foregone conclusion.
Comparing players with serving stats
During tennis matches, players are often compared using statistics such as the percentages of serves which are successful. Imagine a match between Player A and Player B.
In the first set, Player A and Player B are successful with 100% and 92% of their serves respectively. In the second set, these figures are 56% and 48%. Player A clearly looks to be the better server, as they have a higher percentage in each set. However if we look at the two sets in more detail:
| Player A | Player B | |
| First Set | 20/20 | 67/73 |
| Second Set | 45/80 | 13/27 |
| Total | 65/100 | 80/100 |
Table showing successful serves/total serves.
Overall, Player B has an 80% serve success rate, while Player A only manages 65%.
This is an example of Simpson's paradox: a trend which appears in the set-by-set data disappears when the data is combined. This occurs because when we look at the set-by-set percentages, the total number of serves is not taken into account: Player A served more in the second set so their overall percentage will be closer to 56%; Player B served more in the first set so their overall percentage will be closer to 92%.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2014-05-26
With the FIFA World Cup approaching, sticker fans across the world are filling up their official Panini sticker books. This got me wondering: how many stickers should I expect to need to buy to complete my album? And how much will this cost?
How many stickers?
There are 640 stickers required to fill the album. The last 100 stickers required can be ordered from the Panini website.
After \(n\) stickers have been stuck into the album, the probability of the next sticker being the next new sticker is:
$$\frac{640-n}{640}$$
The probability that the sticker after next is the next new sticker is:
$$\frac{n}{640}\frac{640-n}{640}$$
The probability that the sticker after that is the next new sticker is:
$$\left(\frac{n}{640}\right)^2\frac{640-n}{640}$$
Following this pattern, we find that the expected number of stickers bought to find a new sticker is:
$$\sum_{i=1}^{\infty}i \left(\frac{640-n}{640}\right) \left(\frac{n}{640}\right)^i = \frac{640}{640-n}$$
Therefore, to get all 640 stickers, I should expect to buy:
$$\sum_{n=0}^{639}\frac{640}{640-n} = 4505 \mbox{ stickers.}$$
Or, if the last 100 stickers needed are ordered:
$$\sum_{n=0}^{539}\frac{640}{640-n} + 100 = 1285 \mbox{ stickers.}$$
How much?
The first 21 stickers come with the album for £1.99. Additional stickers can be bought in packs of 5 for 50p or multipacks of 30 for £2.75. To complete the album, 100 stickers can be bought for 25p each.
If I decided to complete my album without ordering the final stickers, I should expect to buy 4505 stickers. After the 21 which come with the album, I will need to buy 4484 stickers: just under 897 packs. These packs would cost £411.25 (149 multipacks and 3 single packs), giving a total cost of £413.24 for the completed album.
I'm not sure if I have a spare £413.24 lying around, so hopefully I can reduce the cost of the album by buying the last 100 stickers for £25. This would mean that once I've received the first 21 stickers with the album, I will need to buy 1164 stickers, or 233 packs. These packs would cost £107 (38 multipacks and 5 single packs), giving a total cost of £133.99 for the completed album, significantly less than if I decided not to buy the last stickers.
How many should I order?
The further reduce the number of stickers bought, I could get a friend to also order 100 stickers for me and so buy the last 200 stickers for 25p each. With enough friends the whole album could be filled this way, although as the stickers are more expensive than when bought in packs, this would not be the cheapest way.
If the last 219 or 250 stickers are bought for 25p each, then I should expect to spend £117.74 in total on the album. If I buy any other number of stickers at the end, the expected spend will be higher.
Fortunately, as you will be able to swap your duplicate stickers with your friends, the cost of a full album should turn out to be significantly lower than this. Although if saving money is your aim, then perhaps the Panini World Cup 2014 Sticker Book game would be a better alternative to a real sticker book.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2014-03-29
Following my last post, I wrote to my MP (click to enlarge):
Today I received this reply (click to enlarge):
I'm excited about hearing what the Treasury has to say about it...
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2014-03-19
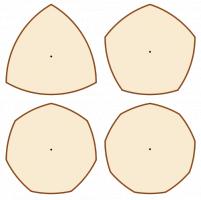
Vending machines identify coins by measuring their width. Circular coins have the same width in every direction, so designers of vending machines do not need to worry about incorrectly rotated coins causing a blockage or being misidentified. But what about seven-sided 20p and 50p coins?
Perhaps surprisingly, 20p and 50p coins also have a constant width, as show by this video. In fact, the sides of any regular shape with an odd number of sides can be curved to give the shape a constant width.
3, 5, 7 and 9 sided shapes of constant width.
Today, a new 12-sided £1 coin was unveiled. One reason for the number of sides was to make the coin easily identified by touch. However, as only polygons with an odd number of sides can be made into shapes of constant width, this new coin will have a different width when measured corner to corner or side to side. This could lead to vending machines not recognising coins unless a new mechanism is added to correctly align the coin before measuring.
Perhaps an 11-sided or 13-sided design would be a better idea, as this would be easily distinguishable from other coins by touch which being a constant width to allow machines to identify it.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2013-07-24
A news story on the BBC Website caught my eye this morning. It reported the following "uncanny coincidence" between a Northern Irish baby and a Royal baby:
But both new mothers share the name Catherine, the same birthday - 9 January - and now their sons also share the same birth date.

I decided to work out just how uncanny this is.
The Office for National Statistics states that 729,674 babies are born every year in the UK. This works out at 1,999 babies born each day, assuming that births are uniformly distributed, so there will be approximately 1,998 babies who share Price Nameless's birthday.
So, what is the chance of the mother of one of these babies having the same birthday as Princess Kate? To work this out I used a method similar to that which is used in the birthday "paradox", which tells us that in a group of 23 people there is a more than 50% chance of two people sharing a birthday, but that's another story.
First, we look at one of our 1,998 mothers. The chance that she shares Princess Kate's birthday is 1/365 (ignoring leap days). The chance that she does not share Princess Kate's Birthday is 364/365.
Next we work out the probability that none of our 1,998 mothers shares Princess Kate's birthday. As our mothers' birthdays are independent we can multiply the probabilities together to do this (this is why we are looking at the probability of not sharing a birthday instead of sharing a birthday). Our probability therefore is \(\left(\frac{364}{365}\right)^{1998} = 0.00416314317\).
Back to the original question, we wanted to know the probability that one of our mothers shares Princess Kate's birthday. To calculate this we do take 0.00416314317 away from 1. This gives 0.99583685682 or 99.6%.
There is a 99.6% chance that there is a resident of the UK who shares the same birthday as Princess Kate and had a child on the same day.
Uncanny.
But let's be fair. The mother in our story is also called Kate. So what are the chances of that? In fact, the same method can be followed, working with the probability of having neither the same birthday or name as Princess Kate.
I think it is safe to assume that this would still be considered news-worthy if our non-princess was called Katie, Cate, Cathryn, Katie-Rose or any other name which is commonly shortened to Kate, so I included a number of variations and used this fantastic tool to find the probability of a mother being called Kate. The data only goes back to 1996, but as the name is dropping in popularity, we can assume that before 1996 at least 1.5% of babies were called Kate. Disregarding males, we can estimate that 3% of mothers are called Kate.
If anyone would like the details of the rest of the calculation, please comment on this post and I will include it here. For anyone who trusts me and isn't curious, I eventually found that the probability of none of our 1,998 mothers share the same name and birthday as Princess Kate is 0.84855028964. So the probability of another Kate having a child on the same day and sharing Princess Kate's birthday is 0.15144971035 or 15.1%. Just over one in seven.
So this is as uncanny as anything else which has a probability of one in seven, such as the Royal baby being born on a Monday (uncanny!).
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment