Blog
2018-04-29
Two years ago, I built a copy of MENACE (Machine Educable Noughts And Crosses Engine). Since then, it's been to many Royal Institution masterclasses, visted Manchester and met David Attenborough. When I'm not showing them off, the 304 matchboxes that make up my copy of MENACE live in this box:
![](javascript:showlimage("menace-box.jpg"))
This box isn't very big, which might lead you to wonder how big MENACE-style machines would be for other games.
Hexapawn (HER)
In A matchbox game learning-machine by Martin Gardner [1], the game of Hexapawn was introduced. Hexapawn is played on a 3×3 grid, and starts with three pawns facing three pawns.
![](javascript:showlimage("hexapawn-start.png"))
The pieces move like pawns: they may be either moved one square forwards into an empty square, or take another pawn diagonally (the pawns are not allowed to move forwards two spaces on their first move, as they can in chess).
You win if one of your pawns reaches the other end of the board. You lose if none of your pieces can move.
The game was invented by Martin Gardner as a good game for his readers to build a MENACE-like machine to play against, as there are only 19 positions that can face player two, so only 19 matchboxes are needed to make HER (Hexapawn Educable Robot). (HER plays as player two, as if player two plays well they can always win.)
Nine Men's Morris (MEME)
In Nine Men's Morris, two players first take turns to place pieces on the board, before taking turns to move pieces to adjacent spaces. If three pieces are placed in a row, a player may remove one of the opponent's pieces. It's a bit like Noughts and Crosses, but with a bit more chance of it not ending in a draw.
In Solving Nine Men's Morris by Ralph Gasser [2], the number of possible game states in Nine Men's Morris is given as approximately \(10^{10}\). To build MEME (Machine Educable Morris Engine), you would need this many matchboxes. These boxes would form a sphere with radius 41m: that's approximately the length of two tennis courts.
![](javascript:showlimage("menace-morris-sphere.png"))
MEME: Machine Educable Morris Engine
As a nice bonus, if you build MEME, you'll also smash the world record for the largest matchbox collection.
Connect 4 (COFFIN)
In Symbolic classification of general two-player games by Stefan Edelkamp and Peter Kissmann [3], the number of possible game states in Connect 4 is given as 4,531,985,219,092. The boxes used to make COFFIN (COnnect Four Fighting INstrument) would make a sphere with radius 302m: approximately the height of the Eiffel Tower.
![](javascript:showlimage("menace-connect4-sphere.png"))
COFFIN: COnnect Four Fighting INstrument
Draughts/Checkers (DOCILE)
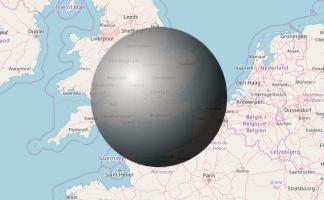
In Solving the game of Checkers by Jonathan Schaeffer and Robert Lake [4], the number of possible game states in Draughts is given as approximately \(5\times10^{20}\). The boxes needed to build DOCILE (Draughts Or Checkers Intelligent Learning Engine) would make a sphere with radius 151km.
![](javascript:showlimage("menace-draughts-map.jpg"))
DOCILE: Draughts Or Checkers Intelligent Learning Engine
If the centre of DOCILE was in London, some of the boxes would be in Sheffield.
Chess (CLAWS)
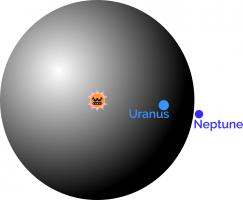
The number of possible board positions in chess is estimated to be around \(10^{43}\). The matchboxes needed to make up CLAWS (Chess Learning And Winning System) would fill a sphere with radius \(4\times10^{12}\)m.
![](javascript:showlimage("menace-chess-sphere.png"))
CLAWS: Chess Learning And Winning System
If the Sun was at the centre of CLAWS, you might have to travel past Uranus on your search for the right box.
Go (MEGA)
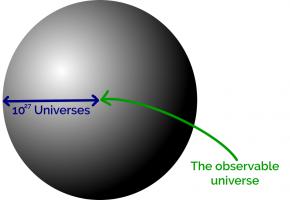
The number of possible positions in Go is estimated to be somewhere near \(10^{170}\). To build MEGA (Machine Educable Go Appliance), you're going to need enough matchboxes to make a sphere with radius \(8\times10^{54}\)m.
![](javascript:showlimage("menace-go-sphere.png"))
MEGA: Machine Educable Go Appliance
The observable universe takes up a tiny space at the centre of this sphere. In fact you could fit around \(10^{27}\) copies of the universe side by side along the radius of this sphere.
It's going to take you a long time to look through all those matchboxes to find the right one...
References
[3] Symbolic classification of general two-player games by Stefan Edelkamp and Peter Kissmann. in Advances in Artificial Intelligence (edited by A.R. Dengel, K. Berns, T.M. Breuel, F. Bomarius, T.R. Roth-Berghofer), 2008. [link]
[4] Solving the game of Checkers by Jonathan Schaeffer and Robert Lake. Games of No Chance 29, 1996. [link]
×1 ×1 ×2 (Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2022-07-31
Kind of like the "Blue Brain Project". They got a worm and fruitfly brain on the computer, I wanted to download the fruitfly brain for 2GB USB stick but it was over 12 TB. They uploaded half a mouse brain on their project so far. Willem
Would Love to play with Coffin/Coffin2. Do you have the code on git or a JS/web version?... been kind of thinking of coding a version that only makes the match boxes as it needs them (to save on memory) but I heard you already have a version with optimizations (and my coding skill is rough at best)
John
Are you aware of any actual implementations of anything in matchboxes, games or otherwise?
Jam
Of course, to make CLAWS, you will have to leave a large gap in the centre of the matchbox sphere, to avoid the very real danger of fire. Furthermore, some redundancy is needed, to replace the boxes which will be damaged by the myriad hard objects which are whizzing around the solar system. For this latter reason alone, I propose that the machine would be impractical to make! ;-D×1 ×1 ×1
g0mrb
×1 ×1 ×1 Add a Comment
2017-06-03
As a child, I was a huge fan of Captain Scarlet and the Mysterons, Gerry Anderson's puppet-starring sci-fi series.
As an adult, I am still a huge fan of Captain Scarlet and the Mysterons.
Set in 2068, the series follows Captain Scarlet and the other members of Spectrum as they attempt to protect Earth from the Mysterons.
One of my favourite episodes of the series is the third: Big Ben Strikes Again.
In this episode, the Mysterons threaten to destroy London. They do this by hijacking a vehicle carrying a nuclear device, and driving it to
a car park. In the car park, the driver of the vehicle wakes up and turns the radio on. Then something weird happens: Big Ben strikes thirteen!
![](javascript:showlimage("radio.jpg"))
The driver turning on the radio. Good to know that BBC Radio 4 will still broadcast at 92-95FM in 2068.
Following this, the driver is knocked out again and wakes up in a side road somewhere. After hearing his story, Captain Blue works out that
the car park must be 1500 yards away from Big Ben. Using this information, Captains Blue and Scarlet manage to track
down the nuclear device and save the day.
![](javascript:showlimage("scarlet_map.jpg"))
A map of London with a circle of radius 1500 yards drawn on it.
After rewatching the episode recently, I realised that it would be possible to recreate this scene and hear Big Ben striking thirteen.
Where does Big Ben strike thirteen?
At the end of the episode, Captain Blue explains to Captain Scarlet that the effect was due to light travelling faster than sound: as the
driver had the radio on, he could hear Ben's bongs both from the tower and through the radio. As radio waves travel faster than
sound, the bongs over the radio can be heard earlier than the sound waves travelling through the air.
Further from the tower, the gap between when the two bongs are heard
is longer; and at just the right distance, the second bong on the radio will be heard at the same time as the first bong from the tower.
This leads to the appearance of thirteen bongs: the first bong is just from the radio, the next eleven are both radio and from the tower, and
the final bong is only from the tower.
Big Ben's bongs are approximately 4.2s apart, sound travels at 343m/s, and light travels at 3×108m/s (this is so fast that it
could be assumed that the radio waves arrive instantly without changing the answer). Using these, we perform the following calculation:
$$\text{time difference} = \text{time for sound to arrive}-\text{time for light to arrive}$$
$$=\frac{\text{distance}}{\text{speed of sound}}-\frac{\text{distance}}{\text{speed of light}}$$
$$=\text{distance}\times\left(\frac1{\text{speed of sound}}-\frac1{\text{speed of light}}\right)$$
$$\text{distance}=\text{time difference}\div\left(\frac1{\text{speed of sound}}-\frac1{\text{speed of light}}\right)$$
$$=4.2\div\left(\frac1{343}-\frac1{3\times10^8}\right)$$
$$=1440\text{m}\text{ or }1574\text{ yards}$$
This is close to Captain Blue's calculation of 1500 yards (and to be fair to the Captain, he had to calculate it in his head in a few seconds).
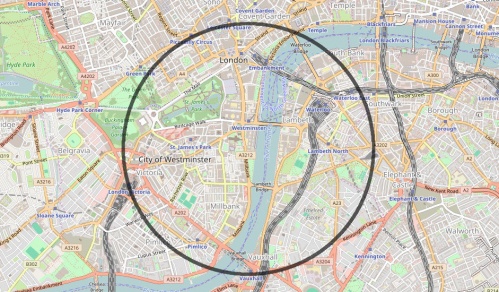
Plotting a circle of this radius centred at Big Ben gives the points where it may be possible to hear 13 bongs.
![](javascript:showlimage("scarlet_my_map.jpg"))
Again, the makers of Captain Scarlet got this right: their circle shown earlier is a very similar size to this one.
To demonstrate that this does work (and with a little help from TD and her camera),
I made the following video yesterday near Vauxhall station. I recommend using earphones to watch it as the later bongs are quite faint.
×3 ×2 ×4 ×3 ×4(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Very late to this but how excellent! My Gerry Andersen experiences were at the start of his output...I even watched Stingray in black and white.×4 ×3 ×3 ×3 ×3
(anonymous)
×4 ×3 ×3 ×3 ×3 Add a Comment
2015-08-27
In 1961, Donald Michie built MENACE (Machine Educable Noughts And Crosses Engine), a machine capable of learning to be a better player of Noughts and Crosses (or Tic-Tac-Toe if you're American). As computers were less widely available at the time, MENACE was built from from 304 matchboxes.
![](javascript:showlimage("menace.jpg"))
Taken from Trial and error by Donald Michie [2]
The original MENACE.
To save you from the long task of building a copy of MENACE, I have written a JavaScript version of MENACE, which you can play against here.
How to play against MENACE
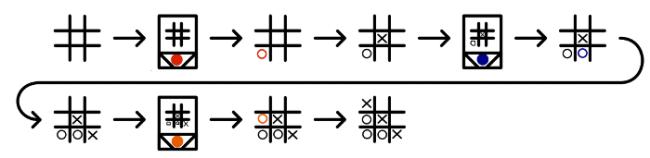
To reduce the number of matchboxes required to build it, MENACE always plays first. Each possible game position which MENACE could face is drawn on a matchbox. A range of coloured beads are placed in each box. Each colour corresponds to a possible move which MENACE could make from that position.
To make a move using MENACE, the box with the current board position must be found. The operator then shakes the box and opens it. MENACE plays in the position corresponding to the colour of the bead at the front of the box.
For example, in this game, the first matchbox is opened to reveal a red bead at its front. This means that MENACE (O) plays in the corner. The human player (X) then plays in the centre. To make its next move, MENACE's operator finds the matchbox with the current position on, then opens it. This time it gives a blue bead which means MENACE plays in the bottom middle.
![](javascript:showlimage("menace-example.png"))
The human player then plays bottom right. Again MENACE's operator finds the box for the current position, it gives an orange bead and MENACE plays in the left middle. Finally the human player wins by playing top right.
MENACE has been beaten, but all is not lost. MENACE can now learn from its mistakes to stop the happening again.
How MENACE learns
MENACE lost the game above, so the beads that were chosen are removed from the boxes. This means that MENACE will be less likely to pick the same colours again and has learned. If MENACE had won, three beads of the chosen colour would have been added to each box, encouraging MENACE to do the same again. If a game is a draw, one bead is added to each box.
Initially, MENACE begins with four beads of each colour in the first move box, three in the third move boxes, two in the fifth move boxes and one in the final move boxes. Removing one bead from each box on losing means that later moves are more heavily discouraged. This helps MENACE learn more quickly, as the later moves are more likely to have led to the loss.
After a few games have been played, it is possible that some boxes may end up empty. If one of these boxes is to be used, then MENACE resigns. When playing against skilled players, it is possible that the first move box runs out of beads. In this case, MENACE should be reset with more beads in the earlier boxes to give it more time to learn before it starts resigning.
How MENACE performs
In Donald Michie's original tournament against MENACE, which lasted 220 games and 16 hours, MENACE drew consistently after 20 games.
![](javascript:showlimage("menace-graph.jpg"))
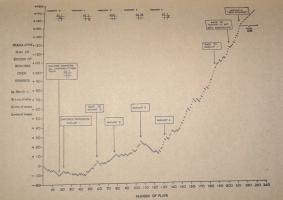
Taken from Trial and error by Donald Michie [2]
![](javascript:showlimage("michie-copy-annot.png"))
Graph showing MENACE's performance in the original tournament. Edit: Added the redrawn graph on the left.
After a while, Michie tried playing some more unusual games. For a while he was able to defeat MENACE, but MENACE quickly learnt to stop losing. You can read more about the original MENACE in A matchbox game learning-machine by Martin Gardner [1] and Trial and error by Donald Michie [2].
You may like to experiment with different tactics against MENACE yourself.
Play against MENACE
I have written a JavaScript implemenation of MENACE for you to play against. The source code for this implementation is available on GitHub.
When playing this version of MENACE, the contents of the matchboxes are shown on the right hand side of the page. The numbers shown on the boxes show how many beads corresponding to that move remain in the box. The red numbers show which beads have been picked in the current game.
The initial numbers of beads in the boxes and the incentives can be adjusted by clicking Adjust MENACE's settings above the matchboxes. My version of MENACE starts with more beads in each box than the original MENACE to prevent the early boxes from running out of beads, causing MENACE to resign.
Additionally, next to the board, you can set MENACE to play against random, or a player 2 version of MENACE.
Edit: After hearing me do a lightning talk about MENACE at CCC, Oliver Child built a copy of MENACE. Here are some pictures he sent me:
![](javascript:showlimage("menace1s.jpg"))
![](javascript:showlimage("menace3s.jpg"))
![](javascript:showlimage("menace4s.jpg"))
Edit: Oliver has written about MENACE and the version he built in issue 03 of Chalkdust Magazine.
Edit: Inspired by Oliver, I have built my own MENACE. I took it to the MathsJam Conference 2016. It looks like this:
![](javascript:showlimage("my_menace.jpg"))
References
[2] Trial and error by Donald Michie. Penguin Science Survey, 1961.
×30 ×28 ×26 ×22 ×24(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
This is very neat. I wonder how long it would take to use that many matches to get all those match boxes.×14 ×14 ×7 ×3 ×3
Duke Nukem
×14 ×14 ×7 ×3 ×3 "When playing against skilled players, it is possible that the first move box runs out of beads. In this case, MENACE should be reset with more beads in the earlier boxes to give it more time to learn before it starts resigning."
If someone were doing this, you could do this automatically to avoid the perception or temptation of the operator to help it along. Instead of "oh, it's dead, let's repopulate the boxes", you could just make it part of the inter-game cleanup, like a garbage collection routine. After all the bead deleting/adding whatever, but before the next game starts, look at all the boxes, make sure that each box contains at least one of each color. Now this weakens the learning algorithm moderately, but it guarantees that it will never get stuck.×3 ×7 ×3 ×4 ×4
If someone were doing this, you could do this automatically to avoid the perception or temptation of the operator to help it along. Instead of "oh, it's dead, let's repopulate the boxes", you could just make it part of the inter-game cleanup, like a garbage collection routine. After all the bead deleting/adding whatever, but before the next game starts, look at all the boxes, make sure that each box contains at least one of each color. Now this weakens the learning algorithm moderately, but it guarantees that it will never get stuck.
(anonymous)
×3 ×7 ×3 ×4 ×4 @Matthew: Thank you for such a quick response. Just to let you know that that link did not work after .../tree/master/output, but I managed to search around for the right files :). In these files MENACE plays the Nought right? and the user plays the Cross?
×2 ×2 ×2 ×2 ×2
(anonymous)
×2 ×2 ×2 ×2 ×2 @Finlay: You can find them at https://github.com/mscroggs/MENACE-pdf.... The files boxes0.pdf to boxes3.pdf are the boxes for a MENACE that plays first.×2 ×4 ×3 ×2 ×3
Matthew
×2 ×4 ×3 ×2 ×3 Add a Comment