Blog
2017-11-14
A few weeks ago, I took the copy of MENACE that I built to Manchester Science Festival, where it played around 300 games against the public while learning to play Noughts and Crosses. The group of us operating MENACE for the weekend included Matt Parker, who made two videos about it. Special thanks go to Matt, plus
Katie Steckles,
Alison Clarke,
Andrew Taylor,
Ashley Frankland,
David Williams,
Paul Taylor,
Sam Headleand,
Trent Burton, and
Zoe Griffiths for helping to operate MENACE for the weekend.
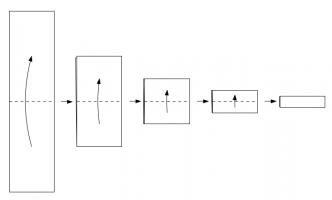
As my original post about MENACE explains in more detail, MENACE is a machine built from 304 matchboxes that learns to play Noughts and Crosses. Each box displays a possible position that the machine can face and contains coloured beads that correspond to the moves it could make. At the end of each game, beads are added or removed depending on the outcome to teach MENACE to play better.
Saturday
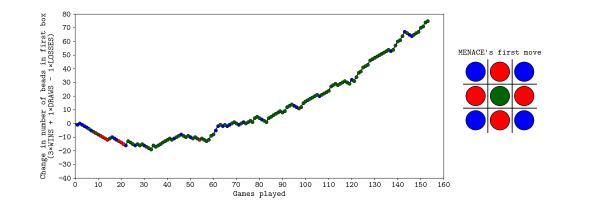
On Saturday, MENACE was set up with 8 beads of each colour in the first move box; 3 of each colour in the second move boxes; 2 of each colour in third move boxes; and 1 of each colour in the fourth move boxes. I had only included one copy of moves that are the same due to symmetry.
The plot below shows the number of beads in MENACE's first box as the day progressed.
![](javascript:showlimage("sat-same-axes.png"))
Sunday
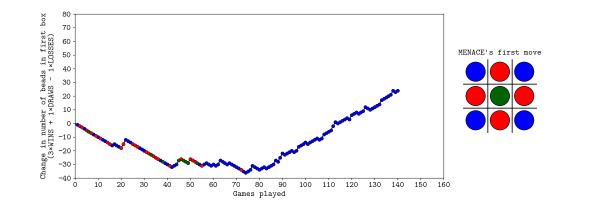
Originally, we were planning to let MENACE learn over the course of both days, but it learned more quickly than we had expected on Saturday, so we reset is on Sunday, but set it up slightly differently. On Sunday, MENACE was set up with 4 beads of each colour in the first move box; 3 of each colour in the second move boxes; 2 of each colour in third move boxes; and 1 of each colour in the fourth move boxes. This time, we left all the beads in the boxes and didn't remove any due to symmetry.
The plot below shows the number of beads in MENACE's first box as the day progressed.
![](javascript:showlimage("sun-same-axes.png"))
The data
You can download the full set of data that we collected over the weekend here. This includes the first two moves and outcomes of all the games over the two days, plus the number of beads in each box at the end of each day. If you do something interesting (or non-interesting) with the data, let me know!
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
2018-11-16
WRT the comment 2017-11-17, and exactly one year later, I had the same thing happen whilst running MENACE in a 'Resign' loop for a few hours, unattended. When I returned, the orange overlay had appeared, making the screen quite difficult to read on an iPad.g0mrb
On the JavaScript version, MENACE2 (a second version of MENACE which learns in the same way, to play against the original) keeps setting the 6th move as NaN, meaning it cannot function. Is there a fix for this?
Lambert
what would happen if you loaded the boxes slightly differently. if you started with one bead corresponding to each move in each box. if the bead caused the machine to lose you remove only that bead. if the game draws you leave the bead in play if the bead causes a win you put an extra bead in each of the boxes that led to the win. if the box becomes empty you remove the bead that lead to that result from the box before
Ian
Hi, I was playing with MENACE, and after a while the page redrew with a Dragon Curves design over the top. MENACE was still working alright but it was difficult to see what I was doing due to the overlay. I did a screen capture of it if you want to see it.
Russ
Add a Comment
2017-03-08
This post appeared in issue 05 of Chalkdust. I strongly
recommend reading the rest of Chalkdust.
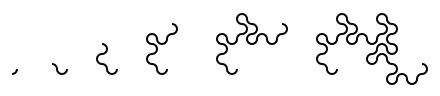
Take a long strip of paper. Fold it in half in the same direction a few times. Unfold it and look at the shape the edge of the paper
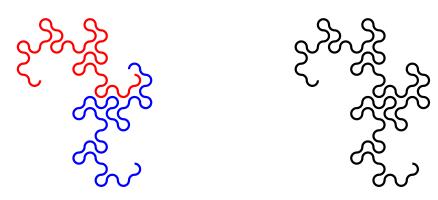
makes. If you folded the paper \(n\) times, then the edge will make an order \(n\) dragon curve, so called because it faintly resembles a
dragon. Each of the curves shown on the cover of issue 05 of Chalkdust is an order 10 dragon
curve.
![](javascript:showlimage("folding-chalkdust.jpg"))
![](javascript:showlimage("labelled-chalkdust.jpg"))
Top: Folding a strip of paper in half four times leads to an order four dragon curve (after rounding the corners). Bottom: A level 10 dragon curve resembling a dragon.
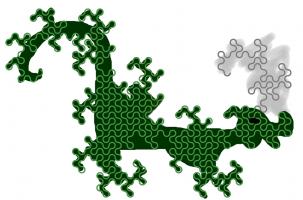
The dragon curves on the cover show that it is possible to tile the entire plane with copies of dragon curves of the same order. If any
readers are looking for an excellent way to tile a bathroom, I recommend getting some dragon curve-shaped tiles made.
An order \(n\) dragon curve can be made by joining two order \(n-1\) dragon curves with a 90° angle between their tails. Therefore, by
taking the cover's tiling of the plane with order 10 dragon curves, we may join them into pairs to get a tiling with order 11 dragon
curves. We could repeat this to get tilings with order 12, 13, and so on... If we were to repeat this ad infinitum we would arrive
at the conclusion that an order \(\infty\) dragon curve will cover the entire plane without crossing itself. In other words, an order
\(\infty\) dragon curve is a space-filling curve.
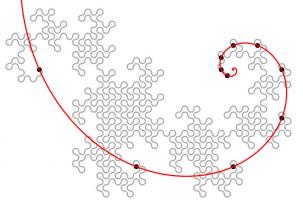
Like so many other interesting bits of recreational maths, dragon curves were popularised by Martin Gardner in one of his Mathematical Games columns in Scientific
American. In this column, it was noted that the endpoints of dragon curves of different orders (all starting at the same point) lie on
a logarithmic spiral. This can be seen in the diagram below.
![](javascript:showlimage("dragons_with_spiral.jpg"))
The endpoints of dragon curves of order 1 to 10 with a logarithmic spiral passing through them.
Although many of their properties have been known for a long time and are well studied, dragon curves continue to appear in new and
interesting places. At last year's Maths Jam conference, Paul Taylor gave a talk about my favourite surprise occurrence of
a dragon.
Normally when we write numbers, we write them in base ten, with the digits in the number representing (from right to left) ones, tens,
hundreds, thousands, etc. Many readers will be familiar with binary numbers (base two), where the powers of two are used in the place of
powers of ten, so the digits represent ones, twos, fours, eights, etc.
In his talk, Paul suggested looking at numbers in base -1+i (where i is the square root of -1; you can find more adventures of i here) using the digits 0 and 1. From right to left, the columns of numbers in this
base have values 1, -1+i, -2i, 2+2i, -4, etc. The first 11 numbers in this base are shown below.
| Number in base -1+i | Complex number |
| 0 | 0 |
| 1 | 1 |
| 10 | -1+i |
| 11 | (-1+i)+(1)=i |
| 100 | -2i |
| 101 | (-2i)+(1)=1-2i |
| 110 | (-2i)+(-1+i)=-1-i |
| 111 | (-2i)+(-1+i)+(1)=-i |
| 1000 | 2+2i |
| 1001 | (2+2i)+(1)=3+2i |
| 1010 | (2+2i)+(-1+i)=1+3i |
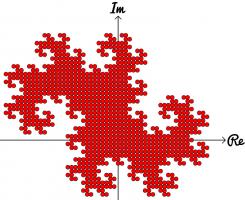
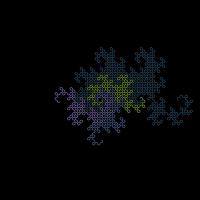
Complex numbers are often drawn on an Argand diagram: the real part of the number is plotted on the horizontal axis and the imaginary part
on the vertical axis. The diagram to the left shows the numbers of ten digits or less in base -1+i on an Argand diagram. The points form
an order 10 dragon curve! In fact, plotting numbers of \(n\) digits or less will draw an order \(n\) dragon curve.
![](javascript:showlimage("complex_dragon_10.jpg"))
Numbers in base -1+i of ten digits or less plotted on an Argand diagram.
Brilliantly, we may now use known properties of dragon curves to discover properties of base -1+i. A level \(\infty\) dragon curve covers
the entire plane without intersecting itself: therefore every Gaussian integer (a number of the form \(a+\text{i} b\) where \(a\) and
\(b\) are integers) has a unique representation in base -1+i. The endpoints of dragon curves lie on a logarithmic spiral: therefore
numbers of the form \((-1+\text{i})^n\), where \(n\) is an integer, lie on a logarithmic spiral in the complex plane.
If you'd like to play with some dragon curves, you can download the Python code used
to make the pictures here.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-06-05
The Game of Life is a cellular automaton invented by John Conway in 1970,
and popularised by Martin Gardner.
In Life, cells on a square grid are either alive or dead. It begins
at generation 0 with some cells alive and some dead. The cells' aliveness in
the following generations are defined by the following rules:
- Any live cell with four or more live neighbours dies of overcrowding.
- Any live cell with one or fewer live neighbours dies of loneliness.
- Any dead cell with exactly three live neighbours comes to life.
Starting positions can be found which lead to all kinds of behaviour:
from making gliders
to generating prime numbers.
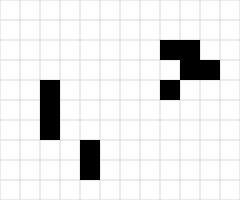
The following starting position is one of my favourites:
![](javascript:showlimage("mslife1.png"))
It looks boring enough, but in the next generation, it will look like this:
![](javascript:showlimage("mslife2.png"))
If you want to confirm that I'm not lying, I recommend the free Game of Life Software Golly.
Going backwards
You may be wondering how I designed the starting pattern above. A first, it looks like a difficult task: each cell can be dead or alive,
so I need to check every possible combination until I find one. The number of combinations will be \(2^\text{number of cells}\). This will
be a very large number.
There are simplifications that can be made, however. Each of the letters above (ignoring the gs) is in a 3×3 block, surrounded
by dead cells. Only the cells in the 5×5 block around this can affect the letter. These 5×5 blocks do no overlap, so can be
calculated seperately. I doesn't take too long to try all the possibilities for these 5×5 blocks. The gs were then made by starting with an o and trying adding cells below.
Can I make my name?
Yes, you can make your name.
I continued the search and found a 5×5 block for each letter. Simply Enter your name in the box below and
these will be combined to make a pattern leading to your name!
×12 ×13 ×11 ×12 ×12(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-03-30
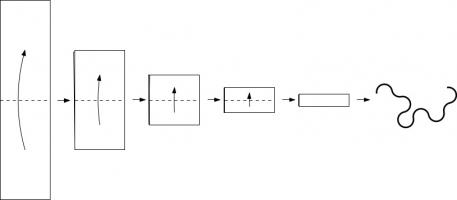
Take a piece of paper. Fold it in half in the same direction many times. Now unfold it. What pattern will the folds make?
![](javascript:showlimage("folding.png"))
I first found this question in one of Martin Gardner's books. At first, you might that the answer will be simple, but if you look at the shapes made for a few folds, you will see otherwise:
![](javascript:showlimage("young-dragons.png"))
Dragon curves of orders 1 to 6.
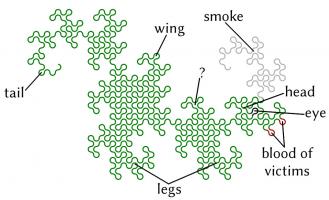
The curves formed are called dragon curves as they allegedly look like dragons with smoke rising from their nostrils. I'm not sure I see the resemblance:
![](javascript:showlimage("drawn-dragon.png"))
An order 10 dragon curve.
As you increase the order of the curve (the number of times the paper was folded), the dragon curve squiggles across more of the plane, while never crossing itself. In fact, if the process was continued forever, an order infinity dragon curve would cover the whole plane, never crossing itself.
This is not the only way to cover a plane with dragon curves: the curves tessellate.
![](javascript:showlimage("dragon-tile.png"))
When tiled, this picture demonstrates how dragon curves tessellate. For a demonstration, try obtaining infinite lives...
Dragon curves of different orders can also fit together:
![](javascript:showlimage("fd1.png"))
![](javascript:showlimage("fd2.png"))
![](javascript:showlimage("fd3.png"))
Drawing dragon curves
To generate digital dragon curves, first notice that an order \(n\) curve can be made from two order \(n-1\) curves:
![](javascript:showlimage("dragon-recursion.png"))
This can easily be seen to be true if you consider folding paper: If you fold a strip of paper in half once, then \(n-1\) times, each half of the strip will have made an order \(n-1\) dragon curve. But the whole strip has been folded \(n\) times, so is an order \(n\) dragon curve.
Because of this, higher order dragons can be thought of as lots of lower order dragons tiled together. An the infinite dragon curve is actually equivalent to tiling the plane with a infinite number of dragons.
If you would like to create your own dragon curves, you can download the Python code I used to draw them from GitHub. If you are more of a thinker, then you might like to ponder what difference it would make if the folds used to make the dragon were in different directions.
×3 ×3 ×3 ×3 ×3(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2016-03-15
This article first appeared in
issue 03 of
Chalkdust. I highly recommend reading the rest of the magazine (and trying
to solve the crossnumber I wrote for the issue).
It all began in December 1956, when an article about hexaflexagons was published in Scientific American. A hexaflexagon is a
hexagonal paper toy which can be folded and then opened out to reveal hidden faces. If you have never made a hexaflexagon, then you should stop
reading and make one right now. Once you've done so, you will understand why the article led to a craze in New York;
you will probably even create your own mini-craze because you will just need to show it to everyone you know.
The author of the article was, of course, Martin Gardner.
![](javascript:showlimage("flexE.jpg"))
A Christmas flexagon.
Martin Gardner was born in 1914 and grew up in Tulsa, Oklahoma. He earned a bachelor's degree in philosophy from the University of Chicago and
after four years serving in the US Navy during the Second World War, he returned to Chicago and began writing. After a few years working on
children's magazines and the occasional article for adults, Gardner was introduced to John Tukey, one of the students who had been involved in
the creation of hexaflexagons.
Soon after the impact of the hexaflexagons article became clear, Gardner was asked if he had enough material to maintain a monthly column.
This column, Mathematical Games, was written by Gardner every month from January 1956 for 26 years until December 1981. Throughout its run,
the column introduced the world to a great number of mathematical ideas, including Penrose tiling, the Game of Life, public key encryption,
the art of MC Escher, polyominoes and a matchbox machine learning robot called MENACE.
Life
Gardner regularly received topics for the column directly from their inventors. His collaborators included Roger Penrose, Raymond Smullyan,
Douglas Hofstadter, John Conway and many, many others. His closeness to researchers allowed him to write about ideas that
the general public were previously unaware of and share newly researched ideas with the world.
In 1970, for example, John Conway invented the Game of Life, often simply referred to as Life. A few weeks later, Conway showed the game to Gardner, allowing
him to write the first ever article about the now-popular game.
In Life, cells on a square lattice are either alive (black) or dead (white). The status of the cells in the next generation of the game is given by the following
three rules:
- Any live cell with one or no live neighbours dies of loneliness;
- Any live cell with four or more live neighbours dies of overcrowding;
- Any dead cell with exactly three live neighbours becomes alive.
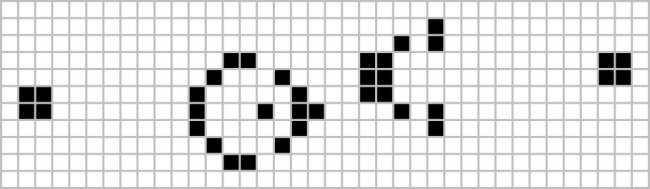
For example, here is a starting configuration and its next two generations:
![](javascript:showlimage("life1.jpg"))
![](javascript:showlimage("life2.jpg"))
![](javascript:showlimage("life3.jpg"))
The first three generations of a game of Life.
The collection of blocks on the right of this game is called a glider, as it will glide to the right and upwards as the generations advance.
If we start Life with a single glider, then the glider will glide across the board forever, always covering five squares: this starting position
will not lead to the sad ending where everything is dead. It is not obvious, however, whether there is a starting
configuration that will lead the number of occupied squares to increase without bound.
![](javascript:showlimage("glider_gun.jpg"))
Gosper's glider gun.
Originally, Conway and Gardner thought that this was impossible, but after the article was published, a reader and mathematician called Bill Gosper
discovered the glider gun: a starting arrangement in Life that fires a glider every 30 generations. As each of these gliders will go on to live
forever, this starting configuration results in the number of live cells
perpetually increasing!
This discovery allowed Conway to prove that any Turing machine can be built within Life: starting
arrangements exist that can calculate the digits of pi, solve equations, or do any other calculation a computer is capable of (although very slowly)!
Encrypting with RSA
To encode the message \(809\), we will use the public key:
$$s=19\quad\text{and}\quad r=1769$$
The encoded message is the remainder when the message to the power of \(s\) is divided by \(r$:
$$809^{19}\equiv\mathbf{388}\mod1769$$
Decrypting with RSA
To decode the message, we need the two prime factors of \(r\) (\(29\) and \(61\)).
We multiply one less than each of these together:
\begin{align*}
a&=(29-1)\times(61-1)\\[-2pt]
&=1680.
\end{align*}
We now need to find a number \(t\) such that \(st\equiv1\mod a\). Or in other words:
$$19t\equiv1\mod 1680$$
One solution of this equation is \(t=619\) (calculated via the extended Euclidean algorithm).
Then we calculate the remainder when the encoded message to the power of \(t\) is divided by \(r\):
$$388^{619}\equiv\mathbf{809}\mod1769$$
RSA
Another concept that made it into Mathematical Games shortly after its discovery was public key cryptography. In mid-1977, mathematicians Ron
Rivest, Adi Shamir and Leonard Adleman invented the method of encryption now known as RSA (the initials of their surnames). Here,
messages are encoded using two publicly shared numbers, or keys. These numbers and the method used to encrypt messages can be publicly shared as
knowing this information does not reveal how to decrypt the message. Rather, decryption of the message requires knowing the prime factors of one of the keys. If this key is the product of two very large
prime numbers, then this is a very difficult task.
Something to think about
Gardner had no education in maths beyond high school, and at times had difficulty understanding the material he was writing about. He believed, however, that this was a strength and not a weakness: his struggle to understand led him to write in a way that other non-mathematicians could follow. This goes a long way to explaining the popularity of his column.
After Gardner finished working on the column, it was continued by Douglas Hofstadter and then AK Dewney before being passed down to Ian Stewart.
Gardner died in May 2010, leaving behind hundreds of books and articles. There could be no better way to end than with something for you to go
away and think about. These of course all come from Martin Gardner's Mathematical Games:
- Find a number base other than 10 in which 121 is a perfect square.
- Why do mirrors reverse left and right, but not up and down?
- Every square of a 5-by-5 chessboard is occupied by a knight.
- Is it possible for all 25 knights to move simultaneously in such a way that at the finish all cells are still occupied as before?
×1 ×1 ×1 ×1 ×1(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment