Blog
2015-03-24
This is the fourth post in a series of posts about tube map folding.
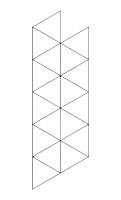
A while ago, I made this (a stellated rhombicuboctahedron):
![](javascript:showlimage("rhombi.jpg"))
Here are some hastily typed instructions for
Matt Parker, who is making one
at this month's Maths Jam. Other people are
welcome to follow these instructions too.
You will need
- 48 tube maps
- glue
Making a module
First, take a tube map and fold the cover over. This will ensure that your
shape will have tube (map and not index) on the outside and you will have
pages to tuck your tabs between later.
![](javascript:showlimage("rh_mp1.jpg"))
Now fold one corner diagonally across to another corner. It does not matter
which diagonal you chose for the first piece but after this all following pieces
must be the same as the first.
![](javascript:showlimage("rh_mp2.jpg"))
Now fold the overlapping bit back over the top.
![](javascript:showlimage("rh_mp3.jpg"))
Turn it over and fold this overlap over too.
![](javascript:showlimage("rh_mp4.jpg"))
You have made one module.
![](javascript:showlimage("rh_mp5.jpg"))
You will need 48 of these and some glue.
Putting it together
By slotting three or four of these modules together, you can make a
pyramid with a triangle or square as its base.
![](javascript:showlimage("rh_mp6.jpg"))
![](javascript:showlimage("rh_mp7.jpg"))
A stellated rhombicuboctahedron is a rhombicuboctahedron with a pyramid, or
stellation on each face. In other words, you now need to build a
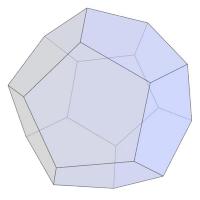
rhombicuboctahedron with the bases of pyramids like these. A rhombicuboctahedron
looks like this:
![](javascript:showlimage("rh_mp_wik.jpg"))
en.wiki User Cyp, CC BY-SA 3.0
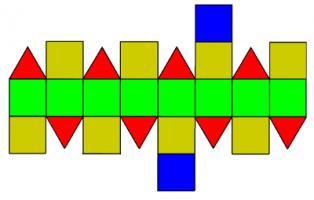
More usefully, its net looks like this:
![](javascript:showlimage("rh_mp_net.png"))
To build a stellated rhombicuboctahedron, make this net, but with each shape
as the base of a pyramid. This is what it will look like 6/48 tube maps in:
![](javascript:showlimage("rh_mp8.jpg"))
If you make on of these, please tweet me a photo so I can see it!
![](javascript:showlimage("rh_mp_fin.jpg"))
Previous post in series
This is the fourth post in a series of posts about tube map folding.
Next post in series
×2 ×2 ×2 ×2 ×2(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
⭐ top comment (2017-10-14) ⭐
I wish you'd make the final stellation of the rhombicuboctahedron! And show us! I know the shapes of the faces but have been stuck two years on the assembly!Roberts, David
×2 ×2 ×2 ×2 ×2 Add a Comment
2015-03-03
This post explains how to make a trihexaflexagon with and images you like on the three
faces.
Making the template
To make a flexagon template with your images on, visit mscroggs.co.uk/flexagons. On this page, you will be
able to choose three images (png, jp(e)g or gif) which will appear on the faces of your flexagon.
Once you have created the template, save and print the image it gives you.
The template may fail to load if your images are too large; so if your template doesn't
appear, resize your images and try again.
Making the flexagon
First, cut out your printed tempate. For this example, I used plain blue, green and purple
images.
![](javascript:showlimage("fold-flex-1.jpg"))
Then fold and glue your template in half lengthways.
![](javascript:showlimage("fold-flex-2.jpg"))
Next, fold diagonally across the blue diamond, being careful to line the fold up with the purple
diamond. This will bring two parts of the purple picture together.
![](javascript:showlimage("fold-flex-3.jpg"))
Do the same again with the blue diamond which has just been folded into view.
![](javascript:showlimage("fold-flex-4.jpg"))
Fold the green triangle under the purple.
![](javascript:showlimage("fold-flex-5.jpg"))
And finally tuck the white triangle under the purple triangle it is covering. This will bring the
two white triangles into contact. Glue these white triangles together and you have made a
flexagon.
![](javascript:showlimage("fold-flex-6.jpg"))
Flexing the flexagon
Before flexing the flexagon, fold it in half through each pair of corners. This will get it
ready to flex in the right places.
![](javascript:showlimage("fold-flex-7.jpg"))
Now fold your flexagon into the following position.
![](javascript:showlimage("fold-flex-8.jpg"))
Then open it out from the centre to reveal a different face.
![](javascript:showlimage("fold-flex-9.jpg"))
This video shows how to flex a
flexagon in more detail.
×2 ×1 ×2 ×2 ×2(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2015-01-31
This is the third post in a series of posts about tube map folding.
In 2012, I folded all the Platonic solids from tube maps. The dodecahedron I made was a little dissapointing:
![](javascript:showlimage("dodec.jpg"))
After my talk at Electromegnetic Field 2014, I was shown the following better method to fold a dodecahedron.
Making the modules
First, take a tube map, cut apart all the pages and cut each page in half.
![](javascript:showlimage("dodec-fold1.jpg"))
Next, take one of the parts and fold it into four
![](javascript:showlimage("dodec-fold2.jpg"))
then lay it flat.
![](javascript:showlimage("dodec-fold3.jpg"))
Next, fold the bottom left corner upwards
![](javascript:showlimage("dodec-fold4.jpg"))
and the top right corner downwards.
![](javascript:showlimage("dodec-fold5.jpg"))
Finally, fold along the line shown below.
![](javascript:showlimage("dodec-fold6.jpg"))
You have now made a module which will make up one edge of the dodecahedron. You will need 30 of these to make the full solid.
![](javascript:showlimage("dodec-fold7.jpg"))
Putting it together
Once many modules have been made, then can be put together. To do this, tuck one of the corners you folded over into the final fold of another module.
![](javascript:showlimage("dodec-fold8.jpg"))
Three of the modules attached like this will make a vertex of the dodecahedron.
![](javascript:showlimage("dodec-fold9.jpg"))
By continuing to attach modules, you will get the shell of a dodecahedron.
![](javascript:showlimage("dodec-foldA.jpg"))
To make the dodecahedron look more complete, fold some more almost-squares of tube map to be just larger than the holes and tuck them into the modules.
![](javascript:showlimage("dodec-foldB.jpg"))
Previous post in series
This is the third post in a series of posts about tube map folding.
Next post in series
×2 ×3 ×3 ×3 ×3(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2014-09-04
Last weekend, I attended Electromagnetic Field, a camp for hackers, geeks, makers and the interested. On the Sunday, I gave a talk on four mathematical ideas/tasks which I have encountered over the past few years: Flexagons, Folding Tube Maps, Braiding and Sine Curves. I'd love to see photos, hear stories, etc from anyone who tries these activities: either comment on here or tweet @mscroggs.
Flexagons
It's probably best to start by showing you what a flexagon is...
What you saw there is called a trihexaflexagon. Tri- because it has three faces; -hexa- because it is a hexagon; and -flexagon because it can be flexed to reveal the other faces.
The story goes that, in 1939, Arthur H. Stone, who was an Englishman studying mathematics at Princeton, was trimming the edges off his American paper to fit in his English folder. He was fiddling with the offcuts and found that if he folded the paper under itself in a loop, he could make a hexagon; and when this hexagon was folded up as we saw, it would open out to reveal a different face.
![](javascript:showlimage("flexagon-slide.png"))
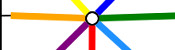
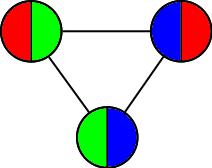
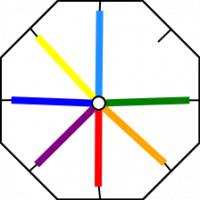
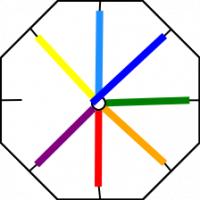
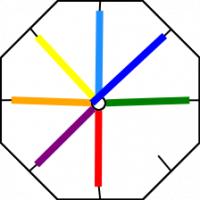
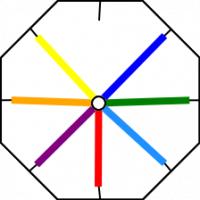
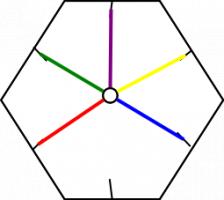
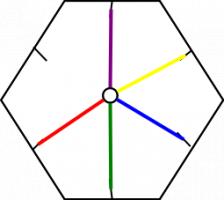
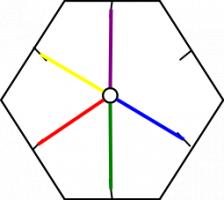
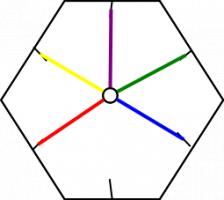
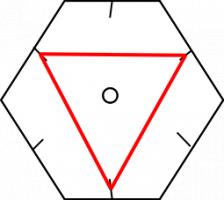
The way it flexes can be shown on a diagram: In the circles, the colour on either side of the flexagon is shown and the lines show flexes which can be made.
![](javascript:showlimage("trihexa.png"))
When Stone showed his flexagon to other students at Harvard, they were equally amazed by it, and they formed what they called 'The Flexagon Committee'. Members of the committee included Richard Feynman, who was then still a graduate student. The committee could meet regularly and soon discovered other flexagons, the first of which was the hexahexaflexagon: Again shaped like a hexagon, but this time with six faces.
![](javascript:showlimage("hexahexa-instr.png"))
A hexahexaflexagon is created by taking a longer strip of paper and rolling it around itself like this. The shorter strip at the end is then folded and glued in the same way the trihexaflexagon was. Once made, the hexahexaflexagon can be flexed. From some positions, the flexagon can be flexed in different ways to reveal different faces. Due to this, finding some of the faces can be quite difficult.
The committee went on to find other flexagons which could be made, again made by first folding into a shorter strip, then folding up like the trihexaflexagon.
The committee later found that hexaflexagons with any number of faces could be made by starting with a certain shaped strip, rolling it up then folding it like a trihexaflexagon.
Resources & further reading
An excellent article by Martin Gardner on flexagons can be found in this book.
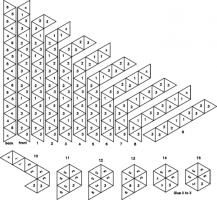
Trihexaflexagon templates (click to enlarge then print):
Our second story starts with me sitting on the tube reading Alex's Adventures in Numberland by Alex Bellos on the tube. In his book, Alex describes how to fold a tetrahedron, or triangle-based pyramid, from two business cards. With no business cards to hand, I picked up two tube maps and followed the steps: first, I folded it corner to corner; then I folded the overlaps over.I made another one of these, but the second a mirror image of the first, slotted them together and I had my tetrahedron.
![](javascript:showlimage("fold1.jpg"))
![](javascript:showlimage("fold2.jpg"))
![](javascript:showlimage("tetrahedron.jpg"))
Then I made a tube map cube by making six squares like so and slotting them together.
![](javascript:showlimage("cube1.jpg"))
![](javascript:showlimage("cube2.jpg"))
![](javascript:showlimage("cube.jpg"))
While making these shapes, I discovered an advantage of tube maps over business cards: Due to the pages, folded tube maps have slots to tuck the tabs into, so the solids are pretty sturdy.
Making these shapes got me wondering: what other Platonic solids could I make?
In 2D, we have regular shapes: shapes with all the sides of the same length and all angles equal. Platonic solids are sort of the 3D equivalent of this: they are 3D shapes where every face is the same regular shape and at each vertex the same number of faces meet.
For example, our tetrahedron is a Platonic solid because every side is a regular triangle, and three triangles meet at every vertex. Our cube is a Platonic solid because every side is a square (which is a regular shape) and three squares meet at every vertex.
In order to fold all the Platonic solids, we must first find out how many there are.
To do this, we're going to start with a triangle, as it is the 2D shape with the smallest number of sides, and make Platonic solids.
If we try to put two triangles at each vertex, then they'll squash flat; so that's no good. We've seen that three triangles at each vertex makes a tetrahedron. If we put four triangles at each vertex then we get an octahedron.
![](javascript:showlimage("octahedron.jpg"))
Five triangles at each vertex gives us an icosahedron.
![](javascript:showlimage("icosahedron.jpg"))
Each angles in an equilateral triangle is 60°. So if we put six triangles at each vertex the angles add up to 360°, a full turn. This means that the triangles will lie flat, giving us a nice pattern for a kitchen floor, but not a solid. Any more than 6 triangles will add up to more than 360 and also not give a solid. So we have found all the Platonic solids whose faces are triangles.
Next, four sided faces. Three squares at each vertex gives us a cube. Four squares at each vertex will add up to 4 times 90°... 360° again, so another kitchen floor and as before we have all the Platonic solids whose faces are squares.
Now moving up again to five sided faces. Three pentagons at each vertex will gives us a dodecahedron, which looks like this.
![](javascript:showlimage("dodecahedron.png"))
This is the best I could do.
(After the talk, I was shown a few better ways to fold pentagons. Watch this space for my attempts...) Now if we try four pentagons around a vertex: the internal angle in a pentagon is 108°. 4 times 108° is 432°. This is more than a full turn, so we don't get a solid.
Moving up again, if we take three hexagons we get another tessellation. Shapes with more than six sides will all have larger angles than this so three make more than a full turn.
Therefore, we have found and folded all the Platonic solids.
In 2012, I posted this on my blog and got the following comment:
![](javascript:showlimage("rhombiwhy.png"))
I'm pretty sure this was a joke, but one hour, 48 tube maps and a lot of glue later:
Resources & further reading
Alex's Adventures in Numberland by Alex Bellos introduced business card folding and takes it further, finishing with a business card Menger sponge.
Braiding
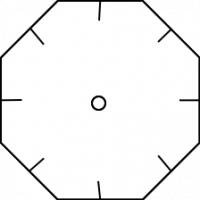
A few months ago, my mother showed my a way to make braids using a cardboard octagon with a slot cut on each side and a hole in the middle.
![](javascript:showlimage("brai1.png"))
To make a braid, seven strands of wool are tied together, fed through the hole, then one tucked into each slot.
![](javascript:showlimage("brai2.png"))
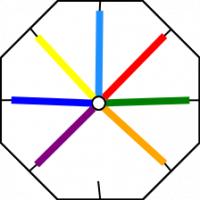
Now, we jump over two strands, pick the third strand and move it to the vacant slot. So first, we jump over the orange and green and move the red strand.
![](javascript:showlimage("brai3.png"))
Then we jump the light blue and yellow and move the dark blue.
![](javascript:showlimage("brai4.png"))
And so on..
![](javascript:showlimage("brai5.png"))
![](javascript:showlimage("brai6.png"))
After a while, the braid looks like this:
![](javascript:showlimage("braid.jpg"))
Once I'd made a few braids, I began to wonder which other numbers of threads could be used to make braids like this. To investigate this I found it useful to represent braids by drawing connections to show where a thread is moved. This shows the first move:
![](javascript:showlimage("brai-second1.png"))
Then the second move:
![](javascript:showlimage("brai-second2.png"))
And so on until you get:
![](javascript:showlimage("brai-second3.png"))
After the octagon, I tried braiding on a hexagon, moving the second thread each time. Here's what happened:
![](javascript:showlimage("brai-third1.png"))
![](javascript:showlimage("brai-third2.png"))
![](javascript:showlimage("brai-third3.png"))
![](javascript:showlimage("brai-third4.png"))
I only moved the yellow and green threads and nothing interesting happened. When I drew this out as before, it demonstrated what had gone wrong: three slots are missed so three threads are never moved.
![](javascript:showlimage("brai-third6.png"))
So we need to find out when slots are missed and when all the slots are hit. To do this, let's call the number of slots \(a\), and let \(b\) be the number thread we pick each time. For example, in the first braid that worked \(a\) was 8 and \(b\) was 3.
First we'll label the slots. Label the slot which starts empty 0, then number anti-clockwise. This numbering puts all the multiples of \(a\) at the bottom slot.
Now let's look at which slots we visit. We start at0, then visit \(b\), then \(2b\), then \(3b\) and so on. We visit all the multiples of \(b\).
Therefore we will reach the bottom slot again and finish our loop when we reach a common multiple of \(a\) and \(b\). The first time this happens will be at the lowest common multiple, or:
$$\mbox{lcm}(a,b)$$
On our way to this slot, we visited one slot for every \(a\) we passed, so the number of slots we have visited is
$$\frac{\mbox{lcm}(a,b)}{a}$$
and we will visit every slot if
$$\frac{\mbox{lcm}(a,b)}{a}=b$$
or, equivalently if
$$\mbox{lcm}(a,b)=ab.$$
This is true when, \(a\) and \(b\) have no common factors, or in other words are coprime; which can be written
$$\mbox{hcf}(a,b)=1.$$
So we've found that if \(a\) is the number of slots and \(b\) is the jump then the braid will not work unless \(a\) and \(b\) are coprime.
For example, if \(a\) is 6 and \(b\) is 2 then 2 is a common factor so the braid fails. And, if \(a\) is 8 and \(b\) is 3 then there are no common factors and the braid works. And, if \(a\) is 12 and \(b\) is 5 then there are no common factors and the braid works.
But, if \(a\) is 5 and \(b\) is 2 then there are no common factors but the braid fails.
The rule I've explained is still correct, and explains why some braids fail. But if \(a\) and \(b\) are coprime, we need more rules to decide whether or not the braid works.
And that's as far as I've got, so I'm going to finish braiding with two open questions: Why does the 5 and 2 braid fail? And for which numbers \(a\) and \(b\) does the braid work?
Sine curves
For the last part of the talk, I did a practical demonstration of how to draw a sine curve using five people.
I told the first person to stand on the spot and the second person to stand one step away, hold a length of string and walk.
![](javascript:showlimage("sine1.gif"))
The third person was instructed to stay in line with the second person, while staying on a vertical line.
![](javascript:showlimage("sine2.gif"))
The fourth person was told to walk in a straight line at a constant speed.
![](javascript:showlimage("sine3.gif"))
And the fifth person had to stay in line with both the third and fourth people. This led them to trace a sine curve.
![](javascript:showlimage("sine4.gif"))
To explain why this is a sine curve, consider the following triangle:
![](javascript:showlimage("sine1p5.gif"))
As our first two people are one step apart, the hypotenuse of this triangle is 1. And so the opposite (vertical) side is equal to the sine of the angle.
I like to finish with a challenge, and this task leads nicely into two challenge questions:
1. How could you draw a cosine curve with five people?
2. How could you draw a tan(gent) curve with five people?
Resources & further reading
People Maths: Hidden Depths is full of this kind of dynamic task involving moving people.
×2 ×2 ×2 ×2 ×2(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment
2013-12-23
Here is a collection of Christmas relates mathematical activities.
Flexagons
I first encountered flexagons sometime around October 2012. Soon after, we used this template to make them at school with year 11 classes who had just taken GCSE papers as a fun but mathematical activity. The students loved them. This lead me to adapt the template for Christmas:
![](javascript:showlimage("xmas-flex.png"))
And here is an uncoloured version of the template on that site if you'd like to colour it yourself and a blank one if you'd like to make your own patterns:
![](javascript:showlimage("flex.png"))
![](javascript:showlimage("blank-flex.png")){kind=spacer}
The excitement of flexagons does not end there. There are templates around for six faced flexagons and while writing this piece, I found this page with templates for a great number of flexagons. In addition, there is a fantastic article by Martin Gardner and a two part video by Vi Hart.
Fröbel stars
I discovered the Fröbel star while searching for a picture to be the Wikipedia Maths Portal picture of the month for December 2013. I quickly found these very good instructions for making the star, although it proved very fiddly to make with paper I had cut myself. I bought some 5mm quilling paper which made their construction much easier. With a piece of thread through the middle, Fröbel starts make brilliant tree decorations.
(Click on one of these icons to react to this blog post)
You might also enjoy...
Comments
Comments in green were written by me. Comments in blue were not written by me.
Add a Comment