Puzzles
Square in a triangle
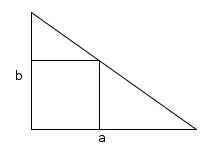
A right-angled triangle has short sides of length \(a\) and \(b\). A square is drawn in the triangle so that two sides lie on the sides of the triangle and a corner lies on the hypotenuse.
What is the length of a side of the square?
Show answer & extension
Hide answer & extension
Call the length of a side of the square \(x\). CAB and CEF are similar triangles, therefore:
$$\frac{EF}{AB}=\frac{EC}{AC}$$
$$\frac{x}{a}=\frac{b-x}{b}$$
$$bx=ab-ax$$
$$x=\frac{ab}{a+b}$$
Extension
Consider a tetrahedron with vertices at \((0,0,0)\), \((a,0,0)\), \((0,b,0)\) and \((0,0,c)\). A cube is placed in the tetrahedron so that three of its faces are in the xy, xz and yz planes and one of its vertices lies on the other face.
What is the length of a side of the cube?
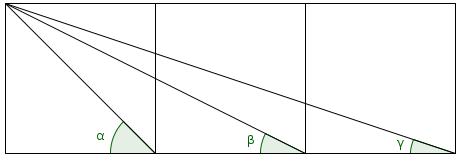
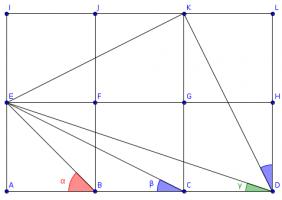
Three squares
The diagram shows three squares with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?
Show answer & extension
Hide answer & extension
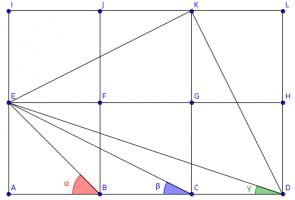
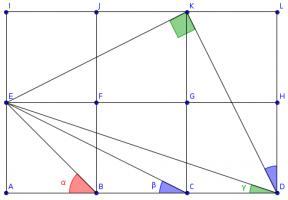
Draw three more squares and add these lines (I have coloured the angles to make equal angles clearer):
Triangles \(ACE\), \(LDK\) and \(IKE\) are congruent, so angle \(KDL\) is equal to \(\beta\).
The congruence of these triangles tells us that angles \(DKL\) and \(EKI\) add up to a right angle, so angle \(EKD\) is also a right angle.
The congruence of the triangles also tells us that \(KD\) and \(KE\) are the same length and so angle \(EDK\) is the angle in an isosceles right-angled triangle. \(\alpha\) is also the angle in an isosceles right-angled triangle, so these two angles are equal.
Therefore \(\alpha+\beta+\gamma=90^\circ\).
Extension
The diagram shows three rhombuses with diagonals drawn on and three angles labelled.
What is the value of \(\alpha+\beta+\gamma\)?
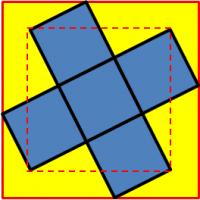
Square cross
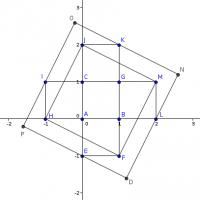
A figure in the shape of a cross is made from five 1 x 1 squares, as shown. The cross is inscribed in a large square whose sides are parallel to the dashed square, formed by four vertices of the cross.
What is the area of the large outer square?
Show answer
Hide answer
The smaller diagonal square is made up of a 1×1 square and four 1×2 right-angled triangles. Therefore its area is 5.
The line FM, and therefore the line DN, has gradient 2. The line JM, and therefore the line ON, has gradient -½. ON passes through (1,2) and DN passes through (2,0). Therefore, DN has equation \(y=2x-4\) and ON has equation \(y=\frac{5}{2}-\frac{1}{2}x\). These lines intersect at \((\frac{13}{5},\frac{6}{5})\), these are the co-ordinates of N. By the same method, the co-ordinates of P are \((-\frac{8}{5},-\frac{1}{5})\).
By Pythagoras' Theorem, The diagonal of the larger square is \(\frac{7\sqrt{10}}{5}\) and so the area of the larger square is 9.8.
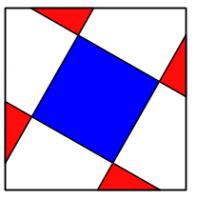
Overlapping triangles
Four congruent triangles are drawn in a square.
The total area which the triangles overlap (red) is equal to the area
they don't cover (blue). What proportion of the area of the large square
does each (purple) triangle take up?
Show answer & extension
Hide answer & extension
Let \(S\) be the area of the large square, \(T\) be the area
of one of the large triangles, \(U\) be one of the red overlaps
and V be the uncovered blue square. We can write
$$S=4T-4U+V$$
as the area of the square is the total of the four triangles,
take away the overlaps as they have been double counted, add
the blue square as it has been missed.
We know that 4U=V, so
$$S=4T-V+V$$
$$S=4T.$$
Therefore one of the triangles covers one quarter of the
square.
Extension
Five congruent triangles are drawn in a regular pentagon. The
total area which the triangles overlap (red) is equal to the area they
don't cover (blue). What proportion of the area of the large pentagon
does each triangle take up?
\(n\) congruent triangles are drawn in a regular \(n\) sided polygon.
The
total
area which the triangles overlap is equal to the area they don't cover.
What proportion of the area of the large \(n\) sided polygon does each
triangle take up?
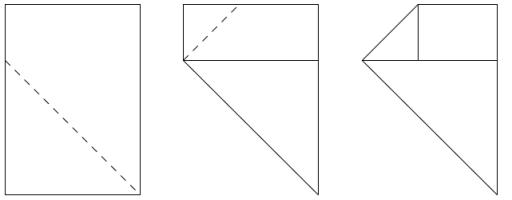
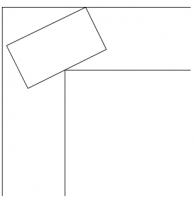
Folding A4 paper
A Piece of
A4 paper is folded as shown:
What shape is made?
Show answer & extension
Hide answer & extension
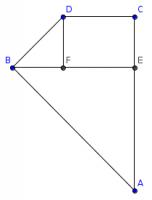
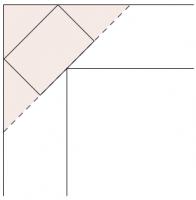
The sides of A4 paper are in the ratio \(1:\sqrt{2}\). Let the width of the paper be 1 unit. This means that the height of the paper is \(\sqrt{2}\) units.
Therefore on the diagram, \(AE=1, BE=1, AC=\sqrt{2}\). By Pythagoras' Theorem, \(AB=\sqrt{2}\), so \(AB=AC\).
\(BF=DF=\sqrt{2}-1\) so by Pythagoras' Theorem again, \(BD=2-\sqrt{2}\). \(CD=1-(\sqrt{2}-1)=2-\sqrt{2}\). Hence, \(CD=BD\) and so the shape is a kite.
Extension
Prove that for a starting rectangle with the sides in any ratio, the resulting shape is a
cyclic quadrilateral.
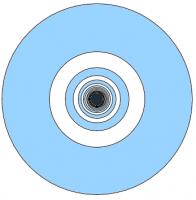
Dartboard
Concentric circles with radii 1, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ... are drawn. Alternate donut-shaped regions are shaded.
What is the total shaded area?
Show answer & extension
Hide answer & extension
The shaded area is:
$$\pi (1)^2 - \pi (\frac{1}{2})^2 + \pi (\frac{1}{3})^2 - \pi (\frac{1}{4})^2 + \pi (\frac{1}{5})^2 - ...$$
$$=\sum_{i=1}^\infty \frac{\pi (-1)^{i-1}}{i^2}$$
$$=\pi\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}$$
$$=\pi\left(\frac{\pi^2}{12}\right)$$
$$=\frac{\pi^3}{12}$$
Extension
Prove that
$$=\sum_{i=1}^\infty \frac{(-1)^{i-1}}{i^2}=\frac{\pi^2}{12}$$
Grand piano
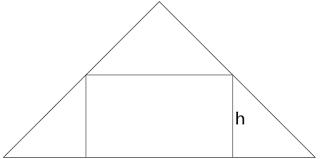
Jack and Jill are moving into a new flat and their grand piano presents a potential problem. Fortunately, it will just pass round the corridor without being tipped or disassembled.
Given that its area, looking down from above, is the largest possible which can be passed around the corner, what is the ratio of its length to its width?
Show answer & extension
Hide answer & extension
When halfway around the corner, the grand piano will look like this:
The problem then is finding the largest area rectangle which fits in the highlighted triangle: an isosceles triangle where the base is twice the height. Let the base be 2 and the height be 1.
If the height of the rectangle is \(h\), then its width is \(2(1-h)\). Therefore its area is \(2h-2h^2\). By differentiation, it can be seen that this is maximum when \(h=\frac{1}{2}\), which means that ratio of the rectangle's length to its width is 2:1.
Extension
If the corner was not a 90° angle, then what is the largest area rectangle which could fit round it?
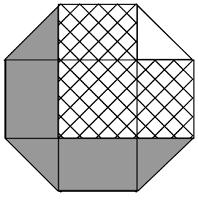
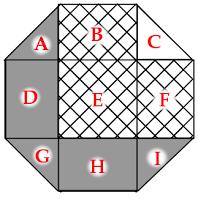
Unit octagon
The diagram shows a regular octagon with sides of length 1. The octagon is divided into regions by four diagonals. What is the difference between the area of the hatched region and the area of the region shaded grey?
Show answer & extension
Hide answer & extension
Name the regions as follows:
\(E\) is a 1×1 square. Placed together, \(A\), \(C\), \(G\) and \(I\) also make a 1×1 square. \(B\) is equal to \(H\) and \(D\) is equal to \(F\).
Therefore \(B+E+F=A+C+D+G+H+I\). Therefore the hatched region is \(C\) larger than the shaded region. The area of \(C\) (and therefore the difference) is \(\frac{1}{4}\).
Extension
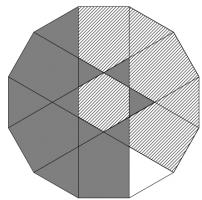
What is the difference between the shaded and the hatched regions in this dodecagon?
![](javascript:showlimage("sq-in-tri.png"))
![](javascript:showlimage("three-squares.png"))
![](javascript:showlimage("three-ans1.png"))
![](javascript:showlimage("three-ans2.png"))
![](javascript:showlimage("three-ans3.png"))
![](javascript:showlimage("three-ans4.png"))
![](javascript:showlimage("three-rhombus.png"))
![](javascript:showlimage("959058_orig.png"))
![](javascript:showlimage("cross+square.png"))
![](javascript:showlimage("overlapping1.png"))
![](javascript:showlimage("overlapping2.png"))
![](javascript:showlimage("folding-a4-paper.png"))
![](javascript:showlimage("kite.png"))
![](javascript:showlimage("dartboard.png"))
![](javascript:showlimage("piano.png"))
![](javascript:showlimage("piano-ans.png"))
![](javascript:showlimage("piano-ans2.png"))
![](javascript:showlimage("octagon.png"))
![](javascript:showlimage("octagon-a1.png"))
![](javascript:showlimage("dodecagon.png"))