Puzzles
Overlapping triangles
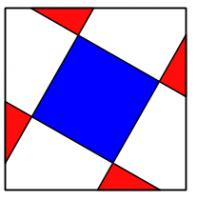
Four congruent triangles are drawn in a square.
The total area which the triangles overlap (red) is equal to the area
they don't cover (blue). What proportion of the area of the large square
does each (purple) triangle take up?
Show answer & extension
Hide answer & extension
Let \(S\) be the area of the large square, \(T\) be the area
of one of the large triangles, \(U\) be one of the red overlaps
and V be the uncovered blue square. We can write
$$S=4T-4U+V$$
as the area of the square is the total of the four triangles,
take away the overlaps as they have been double counted, add
the blue square as it has been missed.
We know that 4U=V, so
$$S=4T-V+V$$
$$S=4T.$$
Therefore one of the triangles covers one quarter of the
square.
Extension
Five congruent triangles are drawn in a regular pentagon. The
total area which the triangles overlap (red) is equal to the area they
don't cover (blue). What proportion of the area of the large pentagon
does each triangle take up?
\(n\) congruent triangles are drawn in a regular \(n\) sided polygon.
The
total
area which the triangles overlap is equal to the area they don't cover.
What proportion of the area of the large \(n\) sided polygon does each
triangle take up?
![](javascript:showlimage("overlapping1.png"))
![](javascript:showlimage("overlapping2.png"))
