Puzzles

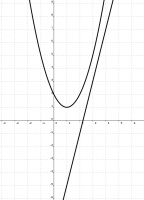
Plotting \(y = 4x - 9\) and \(y = x^2-2x+2\) gives:

As \(p(x)\) has integer coefficients, \(p(3)\) must be an integer. If you click to view a larger version of the image, you'll see that the only option for \(p(3)\) that satisfies \(4x-9<p(x)<x^2-2x+2\) is \(p(3)=4\).

As \(p(x)>4x-9\), it must at least a polynomial of degree 1. As \(p(x)<x^2-2x+2\), it must be at most a polynomial of degree 2. Playing with coefficients, you can see that \(p(x)\) is either \(x^2-2x+1\) or \(4x-8\). \(4x-8\) is negative when \(x=0\), so \(p(x)=x^2-2x+1\) and \(p(23)\) is 484.

The sum of the coefficients can be worked out by substituting \(x=1\) into the polynomial, so the sum of the coefficients is \((3-1)^7\), or 128.

The product of all the solutions is 840.

Expanding \((x-\alpha)(x-\beta)(x-\gamma)(x-\delta)(x-\epsilon)=0\) gives \(x^5 + \dots = \alpha\beta\gamma\delta\epsilon\). As long as the coefficient of \(x^5\) is 1, the constant term when written like this will be the product of all the solutions (for this to always work, you will need to include repeated solutions and complex solutions.)

The equation \(x^8 - 19x^7 + 126x^6 - 294x^5 - 231x^4 + 1869x^3 - 1576x^2 - 1556x + 1680=0\) has eight real solutions. What is the product of all these solutions?