Puzzles
One two three
Each point on a straight line is either red or blue. Show that it's always possible to find three points of the same color in which one is the midpoint of the other two.
Show answer & extension
Hide answer & extension
Pick two points (A and B) of the same colour (say red). Consider the points:
- C such that B is the midpoint of AC.
- D such that A is the midpoint of BD.
- E such that E is the midpoint of AB.
If at least one of C, D or E is red, then three equally spaced red points have been found. If C, D and E are blue, then they are three equally spaced blue points.
Extension
Will there be four equally spaced points of the same colour?
Coloured pins
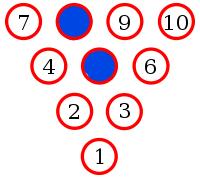
A bowling alley has a mixture of red and blue pins. Ten of these pins are randomly chosen and arranged in a triangle.
Will there always be three pins of the same colour which lie on the vertices of an equilateral triangle?
Show answer & extension
Hide answer & extension
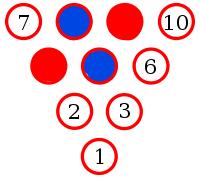
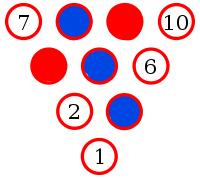
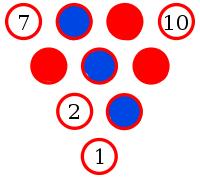
Yes. To show this, let's suppose there is an arrangement of pins with no monochrome triangle.
Let the middle pin be blue (if it is not blue, then swapping all the colours will make it blue without adding/removing monochrome triangles).
Pins 8, 2 and 6 make a triangle. Therefore one of these pins must be blue. By symmetry, any of these situations is equivalent to 8 being blue.
Pins 9 and 4 must be red to prevent a blue triangle.
Pin 3 must be blue to prevent a red triangle.
Pin 6 must be red to prevent a blue triangle.
But now whichever colour 10 is, it will make a monochrome triangle. Therefore there must be three pins of the same colour which lie on the vertices of an equilateral triangle.
Extension
What is the smallest \(n\) such that any mixture of \(n^2\) red and blue pins arranged in a square grid must contain four pins of the same colour which lie on the vertices of a square?
Polygraph
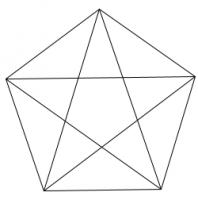
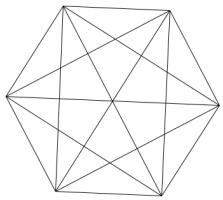
Draw a regular polygon. Connect all its vertices to every other vertex. For example, if you picked a pentagon or a hexagon, the result would look as follows:
Colour the regions of your shape so that no two regions which share an edge are the same colour. (Regions which only meet at one point can be the same colour.)
What is the least number of colours which this can be done with?
Show answer & extension
Hide answer & extension
It can be done with two colours. Let's call these red and blue.
Draw the polygon and colour it red. As each line is added to is, swap the colours on one side of the line which leaving them the same on the other side. At the end of this process you will have any polygon coloured with two colours.
Extension
How many regions will the regular shape be split into by the lines?
![](javascript:showlimage("one-two-three.png"))
![](javascript:showlimage("bowling-pins.png"))
![](javascript:showlimage("bowling-a1.png"))
![](javascript:showlimage("bowling-a2.png"))
![](javascript:showlimage("bowling-a3.png"))
![](javascript:showlimage("bowling-a4.png"))
![](javascript:showlimage("bowling-a5.png"))
![](javascript:showlimage("polygraph2.png"))
![](javascript:showlimage("polygraph1.png"))