Puzzles
8 December
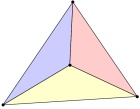
It is possible to arrange 4 points on a plane and draw non-intersecting lines
between them to form 3 non-overlapping triangles:
![](javascript:showlimage("advent2024-8dec.png"))
It is not possible to make more than 3 triangles with 4 points.
What is the maximum number of non-overlapping triangles that can be made by arranging 290 points on a plane
and drawing non-intersecting lines between them?
9 December
The diagram below shows a rectangle. Two of its sides have been coloured blue. A red line has been drawn from two of its vertices to the midpoint of a side.
![](javascript:showlimage("advent2023-9dec.png"))
The total length of the blue lines is 50cm. The total length of the red lines is also 50cm. What is the area of the rectangle (in cm2)?
20 December
![](javascript:showlimage("advent2022-20corrected.png"))
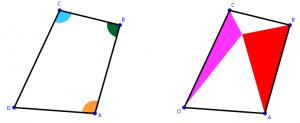
The diagram to the right shows (two copies of) quadrilateral ABCD.
The sum of the angles ABC and BCD (green and blue in quadrilateral on the left) is 180°.
The sum of the angles ABC and DAB (green and orange in quadrilateral on the left) is also 180°.
In the diagram on the right, a point inside the quadrilateral has been used to draw two triangles.
The area of the quadrilateral is 850. What is the smallest that the total area of the two triangles
could be?
10 December
A line is tangent to a curve if the line touches the curve at exactly one point.
The line \(y=-160\,000\) is tangent to the parabola \(y=x^2-ax\). What is \(a\)?
7 December
What is the area of the largest triangle that fits inside a regular hexagon with area 952?
20 December
What is the area of the largest area triangle that has one side of length 32 and one side of length 19?
13 December
![](javascript:showlimage("advent2021-circles.png"))
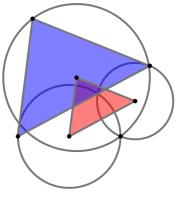
The diagram to the left shows three circles and two triangles. The three circles all meet at one point.
The vertices of the smaller red triangle are at the centres of the circles. The lines connecting the
vertices of the larger blue triangle to the point where all three circles meet are diameters of the
three circles.
The area of the smaller red triangle is 226. What is the area of the larger blue triangle?
7 December
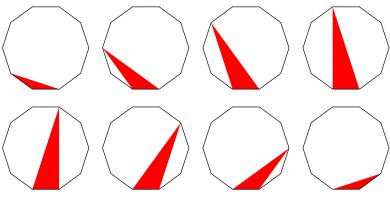
The picture below shows eight regular decagons. In each decagon, a red triangle has been drawn with vertices at three of the vertices of the decagon.
![](javascript:showlimage("advent2021-decagons.png"))
The area of each decagon is 240. What is the total area of all the red triangles?
![](javascript:showlimage("advent2021-dodec-ans.png"))