Advent calendar 2024
25 December
It's nearly Christmas and something terrible has happened: there's been a major malfunction in multiple machines in Santa's toy factory, and
not enough presents have been made. Santa has a backup warehouse full of wrapped presents that can be used in the case of severe emergency, but the warehouse is locked.
You need to help Santa work out the code to unlock the warehouse so that he can deliver the presents before Christmas is ruined for everyone.
The information needed to work out the code to the warehouse is known by Santa and his three most trusted elves: Santa is remembering a three-digit number,
and each elf is remembering a one-digit and a three-digit number. If Santa and the elves all agree that the emergency warehouse should be opened, they can work out the code for the door as follows:
- Santa tells his three-digit number to the first elf.
- The first elf subtracts her three-digit number then multiplies by her one-digit number. She tells her result to the second elf.
- The second elf subtracts his three-digit number then multiplies by his one-digit number. He tells his result to the third elf.
- The third elf subtracts their three-digit number then multiplies by their one-digit number. Their result is a five-digit number that is the code to unlock the warehouse.
But this year, there is a complication: the three elves are on a diplomatic mission to Mars to visit Martian Santa and cannot be contacted, so you need to piece together their
numbers from the clues they have left behind:
21
138 is an elf's 3-digit number.
11
The third elf's 1-digit number is not 2.
18
The first elf's 1-digit number is not 6.
1
144 is an elf's 3-digit number.
15
The third elf's 1-digit number is not 7.
23
The HCF of the first and third elves' 1-digit numbers is not 1, 2, or 8.
12
The second elf's 1-digit number is not 2, 8, or 1.
8
The third elf's 1-digit number is not a factor of 575.
17
The first elf's 1-digit number is not 9.
20
The third elf's 1-digit number is not 4.
7
The third elf's 1-digit number is not 1.
4
The third elf's 1-digit number is not 9.
6
990 is a multiple of an elf's 3-digit number.
3
The first elf's 1-digit number is not 7.
22
The HCF of 851 and the third elf's 3-digit number is 1.
14
The second elf's 1-digit number is not 6, 2, or 5.
24
Santa's number is 444.
9
The first elf's 1-digit number is not 5.
5
The second elf's 1-digit number is not 1, 7, or 9.
10
The second elf's 1-digit number is not 4, 9, or 5.
13
One of the digits of the second elf's 3-digit number is 9.
19
The HCF of 256 and the second elf's 3-digit number is 1.
2
The first elf's 1-digit number is not a factor of 202.
16
The first elf's 1-digit number is not 3.
21
138 is an elf's 3-digit number.
11
The third elf's 1-digit number is not 2.
18
The first elf's 1-digit number is not 6.
1
144 is an elf's 3-digit number.
15
The third elf's 1-digit number is not 7.
23
The HCF of the first and third elves' 1-digit numbers is not 1, 2, or 8.
12
The second elf's 1-digit number is not 2, 8, or 1.
8
The third elf's 1-digit number is not a factor of 575.
17
The first elf's 1-digit number is not 9.
20
The third elf's 1-digit number is not 4.
7
The third elf's 1-digit number is not 1.
4
The third elf's 1-digit number is not 9.
6
990 is a multiple of an elf's 3-digit number.
3
The first elf's 1-digit number is not 7.
22
The HCF of 851 and the third elf's 3-digit number is 1.
14
The second elf's 1-digit number is not 6, 2, or 5.
24
Santa's number is 444.
9
The first elf's 1-digit number is not 5.
5
The second elf's 1-digit number is not 1, 7, or 9.
10
The second elf's 1-digit number is not 4, 9, or 5.
13
One of the digits of the second elf's 3-digit number is 9.
19
The HCF of 256 and the second elf's 3-digit number is 1.
2
The first elf's 1-digit number is not a factor of 202.
16
The first elf's 1-digit number is not 3.
You can to open the door
here.
Show answer
Hide answer
First, let's look at the clues about the elves' 3-digit numbers:
- [1] 144 is an elf's 3-digit number.
- [6] 990 is a multiple of an elf's 3-digit number.
- [21] 138 is an elf's 3-digit number.
- [13] One of the digits of the second elf's 3-digit number is 9.
- [19] The HCF of 256 and the second elf's 3-digit number is 1.
- [22] The HCF of 851 and the third elf's 3-digit number is 1.
The clues on days 1, 6, and 21 tell us that the elves' 3-digit numbers are 144, 138, and one of the factors of 990. Day 19's clue tells us that the second elf's number is odd:
so it must be an odd factor of 990, ie 165 or 495. Day 13's clue tells us that it must be 495.
Day 22's clue tells us that the third elf's 3-digit number cannot be 138 (as 23 is the hcf of 138 and 851), so the third elf's 3-digit number is 144 and the first elf's is 138.
Next, look at all the clues that eliminate options for 1-digit numbers:
- [2] The first elf's 1-digit number is not a factor of 202.
- [3] The first elf's 1-digit number is not 7.
- [4] The third elf's 1-digit number is not 9.
- [5] The second elf's 1-digit number is not 1, 7, or 9.
- [7] The third elf's 1-digit number is not 1.
- [8] The third elf's 1-digit number is not a factor of 575.
- [9] The first elf's 1-digit number is not 5.
- [10] The second elf's 1-digit number is not 4, 9, or 5.
- [11] The third elf's 1-digit number is not 2.
- [12] The second elf's 1-digit number is not 2, 8, or 1.
- [14] The second elf's 1-digit number is not 6, 2, or 5.
- [15] The third elf's 1-digit number is not 7.
- [16] The first elf's 1-digit number is not 3.
- [17] The first elf's 1-digit number is not 9.
- [18] The first elf's 1-digit number is not 6.
- [20] The third elf's 1-digit number is not 4.
After working through these we are left with:
the first elf's 1-digit number is 4 or 8;
the second elf's 1-digit number is 3;
the third elf's 1-digit number is 3, 6, or 8.
There is one more clue about the 1-digit numbers:
- [23] The HCF of the first and third elves' 1-digit numbers is not 1, 2, or 8.
The only option for the first and third elves' 1-digit numbers that satisfies this is first elf 4 and third elf 8.
There is only one clue we are yet to use:
- [24] Santa's number is 444.
In summary:
| Who | 3-digit number | 1-digit number |
| Santa | 444 | — |
| First elf | 138 | 4 |
| Second elf | 495 | 3 |
| Third elf | 144 | 8 |
Using these, we can calcaulate that the code to the door is (((444–138)×4–495)×3–144)×8 = 16344.
24 December
There are 343 three-digit numbers whose digits are all 1, 2, 3, 4, 5, 6, or 7. What is the
mean of all these numbers?
Show answer
Hide answer
The digits 1 to 7 will each appear the same number of times as each other in each position of the number, so each digit of the mean will be the mean of the digits 1 to 7.
Therefore the mean is 444.
23 December
In a grid of squares, each square is friendly with itself and friendly with every square that is horizontally, vertically, or diagonally adjacent to it (and is not friendly with any other squares).
In a 5×5 grid, it is possible to colour 8 squares so that every square is friendly with at least two coloured squares:
It it not possible to do this by colouring fewer than 8 squares.
What is the fewest number of squares that need to be coloured in a
23×23 grid so that every square is friendly with at least two coloured squares?
22 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the largest number that can be formed using the three digits in the red boxes.
| + | | ÷ | | = 3 |
| – | | × | | × | |
| + | | – | | = 6 |
| – | | – | | – | |
| × | | × | | = 16 |
=
1 | | =
13 | | =
16 | |
Show answer
Hide answer
| 9 | + | 3 | ÷ | 4 | = 3 |
| – | | × | | × | |
| 7 | + | 5 | – | 6 | = 6 |
| – | | – | | – | |
| 1 | × | 2 | × | 8 | = 16 |
=
1 | | =
13 | | =
16 | |
The largest number that can be formed with the red digits is 851.
21 December
Noel wants to write a different non-zero digit in each of the five boxes below so that
the products of the digits of the three-digit numbers reading across and down are the same.
What is the smallest three-digit number that Noel could write in the boxes going across?
20 December
p(x) is a polynomial with integer coefficients such that:
- p(0) > 0;
- if x is a real number,
4x – 9 < p(x) < x2 – 2x + 2.
What is p(23)?
Show answer
Hide answer
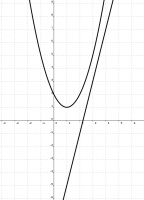
Plotting \(y = 4x - 9\) and \(y = x^2-2x+2\) gives:
As \(p(x)\) has integer coefficients, \(p(3)\) must be an integer. If you click to view a larger version of the image, you'll see that the only option for \(p(3)\) that satisfies
\(4x-9<p(x)<x^2-2x+2\) is \(p(3)=4\).
As \(p(x)>4x-9\), it must at least a polynomial of degree 1. As \(p(x)<x^2-2x+2\), it must be at most a polynomial of degree 2. Playing with coefficients, you can see that
\(p(x)\) is either \(x^2-2x+1\) or \(4x-8\). \(4x-8\) is negative when \(x=0\), so \(p(x)=x^2-2x+1\) and \(p(23)\) is 484.
19 December
There are 9 integers below 100 whose digits are all non-zero and add up to 9:
9, 18, 27, 36, 45, 54, 63, 72, and 81.
How many positive integers are there whose digits are all non-zero and add up to 9?
Show answer & extension
Hide answer & extension
All the integers whose digits are all non-zero and add up to 9 can be made by taking a list of 9 ones, and between each pair deciding whether to move on a digit or not. For example,
1111|111|11 (where | means move on) would represent the number 432; and 1|1|1111111 would represent the number 117.
There are 8 gaps between 9s, so there are 28 = 256 numbers that can be made.
Extension
Why are there not 512 positive integers whose digits are all non-zero and add up to 10?
18 December
If k = 21, then 28k ÷ (28 + k) is an integer.
What is the largest integer k such that 28k ÷ (28 + k) is an integer?
Show answer
Hide answer
If \(k\) is a multiple of 28, then let \(k=28a\) and see that:
$$\frac{28k}{28+k}=\frac{28a}{1+a}$$
This is an integer if either \(a=0\), \(a=1\), or \(1+a\) is a factor of 28. Hence the largest value of \(a\) is 27, leading to \(k\) = 756.
Similar working out can be done for the cases where the hcf of 28 and \(k\) is 14, 7, 2, or 1, and in each case a lower answer would be obtained.
17 December
The number 40 has 8 factors: 1, 2, 4, 5, 8, 10, 20, and 40.
How many factors does the number 226×5×75×112 have?
Show answer
Hide answer
The factors will all be of the form \(2^a\times5^b\times7^c\times11^d\), where
\(0\leqslant a\leqslant26\),
\(0\leqslant b\leqslant1\),
\(0\leqslant c\leqslant5\), and
\(0\leqslant d\leqslant2\). There are 27 choices for \(a\), 2 for \(b\), 6 for \(c\), and 3 for \(d\) giving a total of 27×2×6×3 = 972 factors.
16 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| × | | + | | = 46 |
| ÷ | | + | | + | |
| + | | ÷ | | = 1 |
| ÷ | | × | | × | |
| – | | ÷ | | = 1 |
=
1 | | =
12 | | =
45 | |
Show answer
Hide answer
| 8 | × | 5 | + | 6 | = 46 |
| ÷ | | + | | + | |
| 2 | + | 7 | ÷ | 9 | = 1 |
| ÷ | | × | | × | |
| 4 | – | 1 | ÷ | 3 | = 1 |
=
1 | | =
12 | | =
45 | |
The product of the numbers in the red boxes is 336.
15 December
The number 2268 is equal to the product of a square number (whose last digit is not 0) and the same square number with its digits reversed:
36×63.
What is the smallest three-digit number that is equal to the product of a square number (whose last digit is not 0) and the same square number with its digits reversed?
Show answer
Hide answer
The only three-digit number that is equal to the product of a square number and the same square number with its digits reversed is 16×61 = 976.
14 December
153 is 3375. The last 3 digits of 153 are 375.
What are the last 3 digits of 151234567890?
Show answer
Hide answer
We can look at the first few powers and look for a pattern:
| n | 15n | Last 3 digits of 15n |
| 1 | 15 | 15 |
| 2 | 225 | 225 |
| 3 | 3375 | 375 |
| 4 | 50625 | 625 |
| 5 | 759375 | 375 |
| 6 | 11390625 | 625 |
| 7 | 170859375 | 375 |
| 8 | 2562890625 | 625 |
| 9 | 38443359375 | 375 |
If n is even (and > 2), the last two digits of 15n are 625.
13 December
Today's number is given in this crossnumber. No number in the completed grid starts with 0.
|
|
| Across |
| 1 | Today's number. | (3) |
| 4 | Two times 5A. | (3) |
| 5 | A multiple of 1. | (3) |
|
| Down |
| 1 | Sum of digits is 15. | (3) |
| 2 | Sum of digits is 19. | (3) |
| 3 | Three times 5A. | (3) |
|
Show answer
Hide answer
As 3D is 3 times 5A, and they both share a final digit, their final digit must be 5 or 0.
If it were 0, then 4A would also end zero, so 3D ends in 00. This would mean that 5A also ends 00. 2D therefore would end in 0, but then it's impossible for the sum of 2D's digits to be 19.
Hence, the final digit of 5A cannot be 0, so must be 5:
As 4A is 2 times 5A, it ends in a 0:
3D is a multiple of 3, so must be 105, 405, or 705. These would mean 5A is 35, 135, or 235 (respectively). 5A has three digits so this rules out the first option. Both other options end in 35:
4A is 2 times 5A, so must end in 70:
The sum of the digits of 2D is 19:
If 5A were 135, then 4A would be 270. But then 1D ends with 21 and its digits cannot add to 15. Therefore 5A 235:
4A is 2 times 5A and 3D is 3 times 5A:
The sum of the digits of 1D is 15:
Therefore, today's number is 997.
12 December
Holly picks a three-digit number. She then makes a two-digit number by removing one of the digits.
The sum of her two numbers is 309. What was Holly's original three-digit number?
Show answer
Hide answer
Holly's sum is odd, so she must have removed the units digit and so her calculation was:
$$
\begin{array}{cccc}
a&b&c\\
&a&b&+\\
\hline
3&0&9
\end{array}
$$
\(a\) and \(b\) cannot both be 0, so the must sum in the tens column must've caused a carry into the hundreds column. This means that \(a\) must be 2, and the calculation is:
$$
\begin{array}{cccc}
2&b&c\\
&2&b&+\\
\hline
3&0&9
\end{array}
$$
Two single digits cannot add to 19, so there can't be a carry from the units column into the tens column. This means that \(b\) is 8:
$$
\begin{array}{cccc}
2&8&c\\
&2&8&+\\
\hline
3&0&9
\end{array}
$$
We can see now that \(c\) was 1, so Holly's three digt number was 281.
11 December
There are 6 sets of integers between 1 and 5 (inclusive) that contain an odd number of numbers whose median value is 3:
- {3}
- {1,3,4}
- {2,3,4}
- {1,3,5}
- {2,3,5}
- {1,2,3,4,5}
How many sets of integers between 1 and 11 (inclusive) are there that contain an odd number of numbers whose median value is 5?
Show answer
Hide answer
If the set contains one number, then it must be {5}.
If the set contains three numbers, then it must contain 5, one number less than 5, and one number greater than 5. There are 4 numbers less than 5 and 6 numbers greater than 5 to choose from, giving
a total of 4×6 = 24 sets.
More generally, if the set contains \(2n+1\) numbers, then it must contain 5, \(n\) numbers less than 5, and \(n\) numbers greater than 5.
There are \(\left(\begin{array}{c}4\\n\end{array}\right)\) numbers less than 5 and \(\left(\begin{array}{c}6\\n\end{array}\right)\) numbers greater than 5 to choose from, giving
a total of \(\left(\begin{array}{c}4\\n\end{array}\right)\times\left(\begin{array}{c}6\\n\end{array}\right)\) sets.
In total there are
$$
1+24+
\left(\begin{array}{c}4\\2\end{array}\right)\times\left(\begin{array}{c}6\\2\end{array}\right)
+
\left(\begin{array}{c}4\\3\end{array}\right)\times\left(\begin{array}{c}6\\3\end{array}\right)
+
\left(\begin{array}{c}4\\4\end{array}\right)\times\left(\begin{array}{c}6\\4\end{array}\right)
$$
sets. This is equal to 210.
10 December
A number is a palindrome if it's the same when its digits are written in reverse order.
What is the sum of all the numbers between 10 and 100 that are palindromes?
Show answer
Hide answer
The palindromes between 10 and 100 will be the numbers 11, 22, 33, ..., 99. The sum of these is 495.
9 December
Put the digits 1 to 9 (using each digit exactly once) in the boxes so that the sums are correct. The sums should be read left to right and top to bottom ignoring the usual order of operations. For example, 4+3×2 is 14, not 10.
Today's number is the product of the numbers in the red boxes.
| – | | + | | = 8 |
| – | | ÷ | | ÷ | |
| + | | × | | = 9 |
| × | | ÷ | | ÷ | |
| ÷ | | × | | = 9 |
=
12 | | =
1 | | =
3 | |
8 December
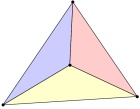
It is possible to arrange 4 points on a plane and draw non-intersecting lines
between them to form 3 non-overlapping triangles:
It is not possible to make more than 3 triangles with 4 points.
What is the maximum number of non-overlapping triangles that can be made by arranging 290 points on a plane
and drawing non-intersecting lines between them?
Show answer
Hide answer
By adding a point inside a triangle, you can turn one triangle into three triangles. By adding a point outside all the current triangles, you can add either
one or two more triangles. As we are after the maximum number of triangles, we will choose to add two triangles for each point we add.
Four points make 3 triangles. Adding 286 more points will add 572 more triangles, giving a total of 575.
7 December
What is the obtuse angle in degrees between the minute and hour hands of a clock at 08:22?
Show answer
Hide answer
Every hour, the hour hand moves 360÷12 = 30°.
Every minute, the hour hand moves 30÷60 = ½° and the minute hand moves 360÷60 = 6°.
At 8:22, the hour hand will be 8×30+22×½ = 251° from the top of the clock
and the minute hand will be 22×6 = 132° from the top of the clock. The angle between the hands will
be 251-132 = 119°.
6 December
The number n has 55 digits. All of its digits are 9.
What is the sum of the digits of n3?
Show answer
Hide answer
We can look for a pattern as we increate the number of 9s that make up n:
| n | n3 |
| 9 | 729 |
| 99 | 970299 |
| 999 | 997002999 |
| 999 | 999700029999 |
| 9999 | 999970000299999 |
If n has k digits, then n3 is
k-1 9s,
followed by a 7,
followed by k-1 0s,
followed by a 2,
followed by k 9s,
The sum of all these digits will by 18k.
Hence, the answer is 18×55 = 990.
5 December
The sum of 11 consecutive integers is 2024. What is the smallest of the 11 integers?
Show answer
Hide answer
Call the smallest number \(n\). The sum of the 11 integers is:
$$n + (n+1) + (n+2) + \dots + (n+10)$$
This simplifies to:
$$11n +55$$
If \(11n+55=2024\), then \(n\) is 179.
4 December
The geometric mean of a set of n numbers is computed by mulitplying all the
numbers together, then taking the nth root.
The factors of 9 are 1, 3, and 9. The geometric mean of these factors is
$$\sqrt[3]{1\times3\times9}=\sqrt[3]{27}=3$$
What is the smallest number where the geometric mean of its factors is 13?
Show answer
Hide answer
Square numbers are the only numbers where the geometric mean of their factors is equal to a whole number,
and in each case the geometric mean will be the square root. Therefore the only number
where the geometric mean of its factors is 13 is 169.
3 December
There are 5 ways to write 5 as the sum of positive odd numbers:
- 1 + 1 + 1 + 1 + 1
- 1 + 1 + 3
- 3 + 1 + 1
- 1 + 3 + 1
- 5
How many ways are there to write 14 as the sum of positive odd numbers?
Show answer
Hide answer
This can be solved by working it out for some examples then looking for the pattern:
| Total | Ways to make | Number of ways |
| 1 | 1 | 1 |
| 2 | 1+1 | 1 |
| 3 | 1+1+1, 3 | 2 |
| 4 | 1+1+1+1, 3+1, 1+3 | 3 |
| 5 | 1+1+1+1+1, 1+1+3, 1+3+1, 3+1+1 | 5 |
| 6 | 1+1+1+1+1+1, 1+1+1+3, 1+1+3+1, 1+3+1+1, 3+1+1+1, 3+3, 5+1, 1+5 | 8 |
The looks like the Fibonacci numbers: every term is the sum of the previous two terms.
Continuing the pattern gives 377 ways to make 14.
To justify why the answer is the Fibonacci numbers, notice that you split the sums for a number n into two sets:
those that end with "+1" and those that end with something else.
Those that end with "+1" are a way of making n-1, plus the one on the end.
Those that don't end with "+1" are a way of making n-2, with two added to the final number.
So the number of ways of making n is
the number of ways of making n-1 plus the number of ways of making n-2.
2 December
14 is the smallest even number that cannot be obtained by rolling two 6-sided dice and finding
the product of the numbers rolled.
What is the smallest even number that cannot be obtained by rolling one hundred 100-sided dice
and finding the product of the numbers rolled?
Show answer
Hide answer
With two 100-sided dice, it is possible to roll the even numbers from 2 to 200 by rolling a two on one die
and 1 to 100 on the other. It is not possible to roll 202, as 101 is prime so cannot be made by multiplying any numbers less than 101.
With one hundred 100-sided dice, the even numbers from 2 to 200 can still be made (by rolling the two dice as before plus lots of ones).
It is still not possible to roll 202, as 101 is still prime.
1 December
Eve writes down five different positive integers. The sum of her integers is 16. What is
the product of her integers?
Show answer
Hide answer
The only five different positive integers with a sum of 16 are 1, 2, 3, 4, and 6.
The product of these is 144.