Puzzles
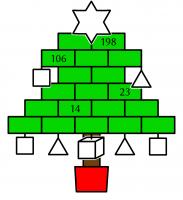
What's the star?
In the Christmas tree below, the rectangle, baubles, and the star at the top each contain a number. The square baubles contain square numbers; the triangle baubles contain triangle numbers; and the cube bauble contains a cube number.
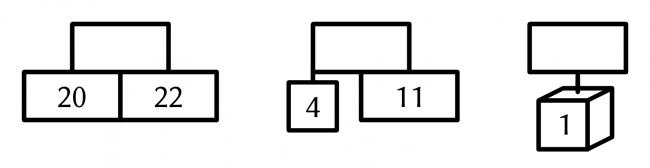
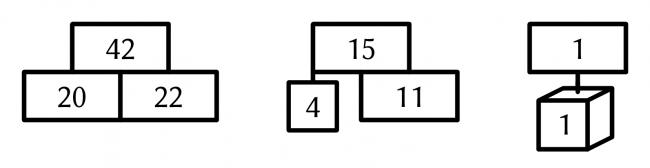
The numbers in the rectangles (and the star) are equal to the sum of the numbers below them. For example, if the following numbers are filled in:
then you can deduce the following:
What is the number in the star at the top of this tree?
You can download a printable pdf of this puzzle here.
Triangles between squares
Prove that there are never more than two triangle numbers between two consecutive square numbers.
Triangle numbers
Source: ATM Mathematics Teaching 239
Let \(T_n\) be the \(n^\mathrm{th}\) triangle number. Find \(n\) such that: $$T_n+T_{n+1}+T_{n+2}+T_{n+3}=T_{n+4}+T_{n+5}$$