Puzzles
14 December
The function \(f(x)=ax+b\) (where \(a\) and \(b\) are real constants) satisfies
$$-x^3+2x^2+6x-9\leqslant f(x)\leqslant x^2-2x+3$$
whenever \(0\leqslant x\leqslant3\). What is \(f(200)\)?
Show answer
Hide answer
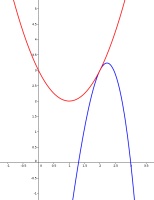
How to get started with this puzzle is easiest to see if we plot the two curves:
We see that the two curves meet at the point (2,3). The only way that the straight line \(f\) can be between the two curves is if it is a tangent to both curves.
By differentiation of another way of finding tangents, you can show that \(a=2\) and \(b=1\). Therefore \(f(200)\) is 399.
19 December
The equation \(352x^3-528x^2+90=0\) has three distinct real-valued solutions.
Today's number is the number of integers \(a\) such that the equation
\(352x^3-528x^2+a=0\) has three distinct real-valued solutions.
Show answer
Hide answer
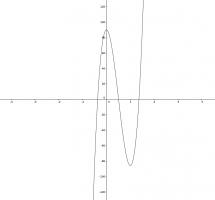
The function \(f(x)=352x^3-528x^2+a\) with \(a=90\) looks like this (click to enlarge):
Adjusting the value of \(a\) will move the curve up and down. The equation \(f(x)=0\) will have three distinct solutions as long as the local minimum is below the \(x\)-axis
and the local maximum is above the \(x\)-axis.
The minimum and maximum are at \(x=1\) and \(x=0\). The difference between \(f(1)\) and \(f(0)\) is 176. This means that there are 175 possible integer values of \(a\) (as the endpoints are not included).
![](javascript:showlimage("advent2023sol-14dec.png"))
![](javascript:showlimage("advent2021-cubic.png"))