Puzzles
2 December
Holly adds up the first six even numbers, then adds on half of the next even number. Her total is 49.
Next, Holly adds up the first \(n\) even numbers then adds on half of the next even number. This time, her total is 465124. What is \(n\)?
21 December
Arrange the digits 1–9 (using each digit exactly once) so that the three digit number in:
the middle row is a prime number;
the bottom row is a square number;
the left column is a cube number;
the middle column is an odd number;
the right column is a multiple of 11.
The 3-digit number in the first row is today's number.
| today's number | |||
| prime | |||
| square | |||
| cube | odd | multiple of 11 |
11 December

This puzzle is inspired by a puzzle Woody showed me at MathsJam.
Today's number is the number \(n\) such that $$\frac{216!\times215!\times214!\times...\times1!}{n!}$$ is a square number.
Square and cube endings
Source: UKMT 2011 Senior Kangaroo
How many positive two-digit numbers are there whose square and cube both end in the same digit?
16 December
There are 204 squares (of any size) in an 8×8 grid of squares. Today's number is the number of rectangles (of any size) in a 2×19 grid of squares
14 December
There are 204 squares (of any size) in an 8×8 grid of squares. Today's number is the number of squares in a 13×13 grid of squares
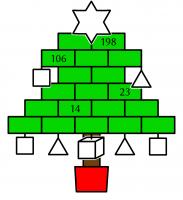
What's the star?
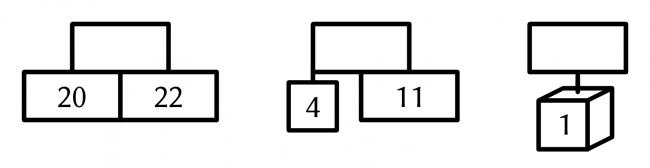
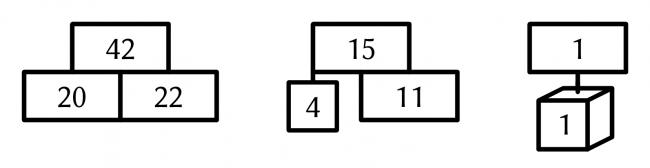
In the Christmas tree below, the rectangle, baubles, and the star at the top each contain a number. The square baubles contain square numbers; the triangle baubles contain triangle numbers; and the cube bauble contains a cube number.
The numbers in the rectangles (and the star) are equal to the sum of the numbers below them. For example, if the following numbers are filled in:
then you can deduce the following:
What is the number in the star at the top of this tree?
You can download a printable pdf of this puzzle here.
Square pairs
Source: Maths Jam
Can you order the integers 1 to 16 so that every pair of adjacent numbers adds to a square number?
For which other numbers \(n\) is it possible to order the integers 1 to \(n\) in such a way?