Puzzles
Archive
Show me a random puzzle Most recent collections
Sunday Afternoon Maths LXVI
Cryptic crossnumber #2Sunday Afternoon Maths LXV
Cryptic crossnumber #1Breaking Chocolate
Square and cube endings
Sunday Afternoon Maths LXIV
Equal lengthsDigitless factor
Backwards fours
Sunday Afternoon Maths LXIII
Is it equilateral?Cube multiples
List of all puzzles
Tags
time geometry 2d shapes 3d shapes numbers spheres trigonometry complex numbers algebra lines graphs coordinates odd numbers fractions differentiation calculus folding tube maps ellipses triangle numbers money bases triangles squares area square numbers chess probability circles averages speed sport multiples dates factors parabolas functions logic cards games people maths shape prime numbers irreducible numbers probabilty angles proportion dice integration sum to infinity dodecagons hexagons multiplication factorials coins shapes regular shapes colouring grids floors integers rugby crosswords percentages digits sums christmas square roots surds doubling quadratics indices symmetry arrows addition cube numbers star numbers rectangles chocolate cryptic clues cryptic crossnumbers crossnumbers wordplay clocks menace routes taxicab geometry remainders chalkdust crossnumber palindromes sequences means unit fractions division planes volume number partitions ave pascal's triangle mean advent perfect numbers6 December
\(p(x)\) is a quadratic with real coefficients. For all real numbers \(x\),
$$x^2+4x+14\leq p(x)\leq 2x^2+8x+18$$
\(p(2)=34\). What is \(p(6)\)?
Between quadratics
Source: Luciano Rila (@DrTrapezio)
\(p(x)\) is a quadratic polynomial with real coefficients. For all real numbers \(x\),
$$x^2-2x+2\leq p(x)\leq 2x^2-4x+3$$
\(p(11)=181\). Find \(p(16)\).
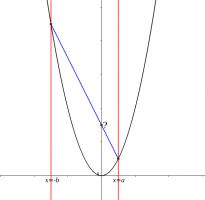
Parabola
Source: Alex Through the Looking-Glass: How Life Reflects Numbers and Numbers Reflect Life by Alex Bellos
On a graph of \(y=x^2\), two lines are drawn at \(x=a\) and \(x=-b\) (for \(a,b>0\). The points where these lines intersect the parabola are connected.
![](javascript:showlimage("parabola.png"))
What is the y-coordinate of the point where this line intersects the y-axis?
© Matthew Scroggs 2018