Puzzles
The ace of spades
I have three packs of playing cards with identical backs. Call the packs A, B and C.
I draw a random card from pack A and shuffle it into pack B.
I now turn up the top card of pack A, revealing the Queen of Hearts.
Next, I draw a card at random from pack B and shuffle it into pack C. Then, I turn up the top card of pack B, revealing another Queen of Hearts.
I now draw a random card from pack C and place it at the bottom of pack A.
What is the probability that the card at the top of pack C is the Ace of Spades?
Show answer
Hide answer
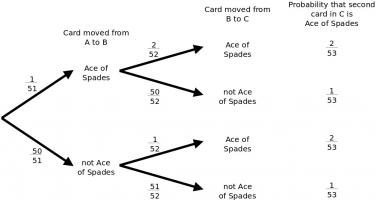
The problem can be expressed using the following probability tree:
The probability that the card turned over from C is an Ace of Spades is:
$$\frac{1\times 2\times 2+1\times 50\times 1+50\times 1\times 2+50\times 51\times 1}{51\times 52\times 53}$$
$$=\frac{52}{51\times 53}$$
Whist
Messrs. Banker, Dentist, Apothecary and Scrivener played whist last night. (whist is a four player card game where partners sit opposite each other.) Each of these gentlemen is the namesake of another's vocation.
Last night, the apothecary partnered Mr. Apothecary; Mr. Banker's partner was the scrivener; on Mr. Scrivener's right sat the dentist.
Who sat on the banker's left?
Show answer & extension
Hide answer & extension
Represent each player by a compass point. Let B, D, A and S represent Messrs. Banker, Dentist, Apothecary and Scrivener respectively and b, d, a and s represent the four jobs.
Mr. Banker (B) partners the scrivener (s). Let B sit at West. This means s sits at East. As no other player can also be B or s, the table looks like this:
The dentist (d) sits on Mr. Scrivener's (S) right. East cannot be S, so North cannot be d. East cannot be d, so South cannot be S.
By elimination, only North can be S. This means that d must sit to the right of North (at West):
A and a are partners. This is only possible if A is South and a is North:
Therefore, Mr. Banker the dentist sits to the left of the banker.
Extension
If each person is partnered with their job namesake, how many possible combinations of names and jobs are possible?