Puzzles
12 December
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
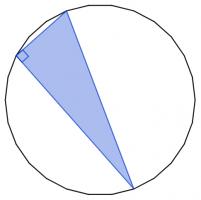
These three vertices form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
Show answer
Hide answer
The vertices of the 26-gon lie on a circle. The triangle is therefore right-angled if (and only if) the longest side is a diameter of the circle.
In other words, the triangle is right angled if (and only if) two of its vertices are opposite vertices of the 26-gon.
There are 13 different pairs of opposite points on the 26-gon. For each of these, there are 24 remaining vertices that could be the third vertex of the triangle.
Therefore there are 13×24=312 different right angled triangles.
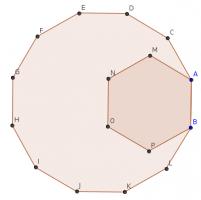
Dodexagon
In the diagram, B, A, C, D, E, F, G, H, I, J, K and L are the vertices of a regular dodecagon and B, A, M, N, O and P are the vertices of a regular hexagon.
Show that A, M and E lie on a straight line.
Show answer & extension
Hide answer & extension
The interior angle of a regular hexagon is 120°. The interior angle of a regular dodecagon is 150°. Therefore angle CAM is 30°.
Now, consider the quadrilateral ACDE. This quadrilateral is symmetric (as the dodecagon is regular) so the angles CAE and DEA are equal. Hence:
$$360 = CAE+DEA+ACD+CDE\\
= 2CAE + 2\times 150\\
2CAE = 60\\
CAE=30
$$
The angles CAM and CAE are equal, so A, M and E lie on a straight line.
Extension
The vertices \(P_1\), \(P_2\), ..., \(P_n\) make up a regular \(n\)-gon and \(Q_1\), \(Q_2\), ..., \(Q_m\) make up a regular \(m\)-gon, with \(P_1=Q_1\) and \(P_2=Q_2\).
The vertices \(P_2\), \(Q_3\) and \(P_5\) lie on a straight line. What is the relationship between \(m\) and \(n\)?
![](javascript:showlimage("advent2018-12.png"))
![](javascript:showlimage("dodexagon.png"))