Puzzles
20 December
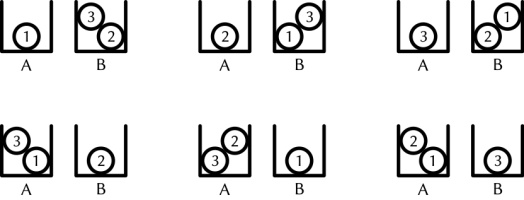
There are 6 different ways that three balls labelled 1 to 3 can be put into two boxes labelled
A and B so that no box is empty:
How many ways can five balls labelled 1 to 5 be put into four boxes labelled A to D so that
no box is empty?
Show answer
Hide answer
One method for putting the five balls into the four boxes is:
pick one of the balls (there are 5 ways to do this), then put the other four balls into boxes with one in each box (there are 4! ways to do this), then
put the picked ball into a box (there are 4 ways to do this). This method gives exactly two ways of obtaining each possible arrangement, so the number of
ways is \(5\times4!\times4\div2\) or 240.
22 December
There are 12 ways of placing 2 tokens on a 2×4 grid so that no two tokens are next to each other horizontally, vertically or diagonally:
Today's number is the number of ways of placing 2 tokens on a 2×21 grid so that no two tokens are next to each other horizontally, vertically or diagonally.
Show answer
Hide answer
The two tokens must be in two non-adjacent columns. There are ½×21×20 ways of picking two different columns. 20 of these ways will give two adjacent columns,
so there are ½×21×20–20=190 ways to pick the columns.
Once the columns are picked there are four choices for the rows to place the tokens in (up and up, up and down, down and up, down and down). 4×190=760.
24 December
There are six ways to put two tokens in a 3 by 3 grid so that the diagonal from the top left to the bottom right is a line of symmetry:
Today's number is the number of ways of placing two tokens in a 29 by 29 grid so that the diagonal from the top left to the bottom right is a line of symmetry.
Show answer
Hide answer
Either both pieces must be on the diagonal, or one pieces is in the lower right half and the other is in the reflected position in the upper right half.
There are \(\left(\begin{array}{c}29\\2\end{array}\right)=406\) ways to pick two squares on the diagonal. There are 406 squares below the diagonal.
Therefore there are 406+406 = 812 ways to arrange the pieces.
6 December
There are 12 ways of placing 2 tokens on a 2×4 grid so that no two tokens are next to each other horizonally, vertically or diagonally:
Today's number is the number of ways of placing 5 tokens on a 2×10 grid so that no two tokens are next to each other horizonally, vertically or diagonally.
Show answer
Hide answer
First, consider placing 5 tiles in a 1×9 grid. There is only one way to do this:
To get the number of ways of placing 5 tiles in a 1×10 grid, imagine adding an extra blank square to either the start or end of the grid or between two of the counters.
There are 6 places this tile could be inserted leading to 6 arrangements of 5 tiles in a 1×10 grid.
For 5 tiles in a 2×10 grid, you can first pick the columns the tiles go in (as a tile being in a column means nothing can be placed the columns either side, the number of ways to pick
columns is the same and the number of wats to arrange 5 tokens in a 1×10 grid). For each of these column choices, there are two locations for each tile (top or bottom).
This leads to a total number of arrangements of 6×25=192.
|