Puzzles
23 December
Today's number is the area of the largest area rectangle with perimeter 46 and whose sides are all integer length.
12 December
There are 2600 different ways to pick three vertices of a regular 26-sided shape. Sometimes the three vertices you pick form a right angled triangle.
These three vertices form a right angled triangle.
Today's number is the number of different ways to pick three vertices of a regular 26-sided shape so that the three vertices make a right angled triangle.
Show answer
Hide answer
The vertices of the 26-gon lie on a circle. The triangle is therefore right-angled if (and only if) the longest side is a diameter of the circle.
In other words, the triangle is right angled if (and only if) two of its vertices are opposite vertices of the 26-gon.
There are 13 different pairs of opposite points on the 26-gon. For each of these, there are 24 remaining vertices that could be the third vertex of the triangle.
Therefore there are 13×24=312 different right angled triangles.
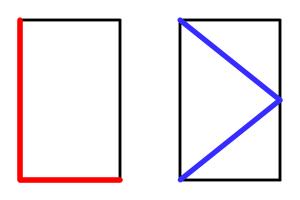
Equal lengths
The picture below shows two copies of the same rectangle with red and blue lines. The blue line visits the midpoint of the opposite side. The lengths shown in red and blue are of equal length.
What is the ratio of the sides of the rectangle?
Show answer
Hide answer
Let \(a\) be the height of the rectangle and \(b\) be the width.
The length of the red line is \(a+b\). The length of the blue line is \(2\sqrt{a^2+\frac{b^2}4}\). These are equal so:
\begin{align}
a+b&=2\sqrt{a^2+\frac{b^2}4}\\
(a+b)^2&=4\left(a^2+\frac{b^2}{4}\right)\\
a^2+2ab+b^2&=4a^2+b^2\\
0&=3a^2-2ab\\
0&=3a-2b\\
2b&=3a
\end{align}
Therefore the ratio of the sides is 2:3.
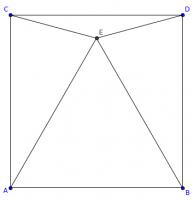
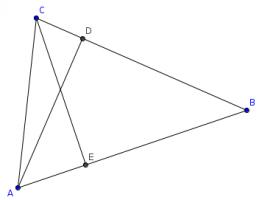
Is it equilateral?
In the diagram below, \(ABDC\) is a square. Angles \(ACE\) and \(BDE\) are both 75°.
Is triangle \(ABE\) equilateral? Why/why not?
Show answer
Hide answer
The triangle is equilateral.
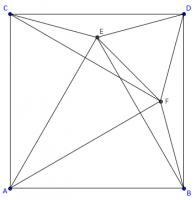
To see why, add a copy of point \(E\) rotated by 90°. This is labelled \(F\) on the diagram below.
Angles \(BDE\) and \(CDF\) are both 75°. Therefore angles \(CDE\) and \(BDF\) are both 15°. This means that angle \(FDE\) is 60°.
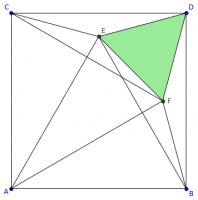
Line \(AD\) is a line of symmetry of the diagram, so angles \(DFE\) and \(DEF\) are equal and both 60°. Therefore, triangle DEF is equilateral. This triangle is show in green in the diagram below.
Lines \(EF\), \(DF\) and \(BF\) are all equal length, so triangles \(BFE\) and \(BFD\) are isosceles.
Angles \(BDF\) and \(FBD\) are both 15°. Angles \(FBE\) and \(FEB\) are equal, and the angles in triangle \(BED\) add to 180°: this means that angle \(FBE\) is 15°.
Angles \(FBE\) and \(FBD\) are both 15°, and so angle \(EBD\) is 30°. Angles \(EBD\) and \(ABE\) add to 90°, and so angle \(ABE\) is 60°.
By symmetry, angle \(BAE\) is also 60°. Angle \(BEA\) must therefore also be 60°, so triangle \(ABE\) is equilateral.
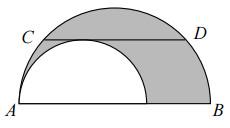
Two semicircles
The diagram shows two semicircles.
\(CD\) is a chord of the larger circle and is parallel to \(AB\). The length of \(CD\) is 8m. What is the area of the shaded region (in terms of \(\pi\))?
Show answer & extension
Hide answer & extension
The question does not fix the length of \(AB\), yet implies that there is a unique answer. Therefore we can take \(AB\) to be any length we like and expect the right answer. If \(AB\) is 8m long, then the unshaded semicircle has no area. Therefore the shaded area is \(\tfrac12\pi\times4^2=8\pi\)m.
Extension
How would you calculate the area if you don't assume that the length of \(AB\) doesn't affect the area?
5 December
How many different triangles are there with a perimeter of 100 and each side
having an integer length?
(different = not rotations or reflections)
1 December
What is area of the largest area rectangle which will fit in a circle of radius 10?
Show answer
Hide answer
The largest rectangle will be a square. 20 (double the radius) will be the length of its diagonal.
By Pythagoras' Theorem, the sides of the square are \(10\sqrt{2}\). Therefore the area of the square is 200.
Cutting corners
The diagram below shows a triangle \(ABC\). The line \(CE\) is perpendicular to \(AB\) and the line \(AD\) is perpedicular to \(BC\).
The side \(AC\) is 6.5cm long and the lines \(CE\) and \(AD\) are 5.6cm and 6.0cm respectively.
How long are the other two sides of the triangle?
Show answer
Hide answer
Let \(A\), \(B\) and \(C\) represent the angles at points \(A\), \(B\) and \(C\). Looking at triangle \(ACE\) gives:
$$\sin A=\frac{5.6}{6.5}$$
And triangle \(ACD\) gives:
$$\sin C=\frac{6.0}{6.5}$$
Using Pythagoras' Theorem to find the missing sides in these triangles also gives:
$$\cos A=\frac{3.3}{6.5}$$
$$\cos C=\frac{2.5}{6.5}$$
We can use these to find \(\sin B\):
$$\begin{array}{rl}
\sin B&=\sin(\pi-A-C)\\
&=\sin(A+B)\\
&=\sin A\cos C + \cos A\sin C\\
&=\frac{5.6}{6.5}\frac{2.5}{6.5}+\frac{6.0}{6.5}\frac{3.3}{6.5}\\
&=\frac{33.8}{6.5^2}
\end{array}$$
Now the missing sides can be found using the sine rule:
$$\begin{array}{rl}
CB&=\frac{CA\sin A}{\sin B}\\
&=\frac{6.5\times\frac{5.6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times5.6}{33.8}\\
&=7\text{cm}
\end{array}$$
$$\begin{array}{rl}
AB&=\frac{CA\sin C}{\sin B}\\
&=\frac{6.5\times\frac{6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times6}{33.8}\\
&=7.5\text{cm}
\end{array}$$
![](javascript:showlimage("advent2018-12.png"))
![](javascript:showlimage("rectangles506.png"))
![](javascript:showlimage("square-cd07.png"))
![](javascript:showlimage("square-cd07-sol1.png"))
![](javascript:showlimage("square-cd07-sol2.png"))
![](javascript:showlimage("two-semicircles.jpg"))
![](javascript:showlimage("cut-corn.png"))