Puzzles
Grand piano
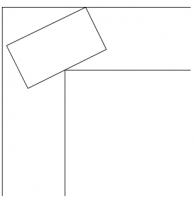
Jack and Jill are moving into a new flat and their grand piano presents a potential problem. Fortunately, it will just pass round the corridor without being tipped or disassembled.
Given that its area, looking down from above, is the largest possible which can be passed around the corner, what is the ratio of its length to its width?
Show answer & extension
Hide answer & extension
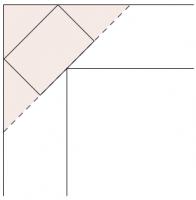
When halfway around the corner, the grand piano will look like this:
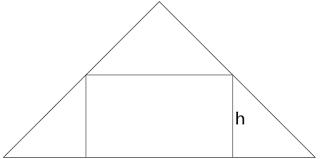
The problem then is finding the largest area rectangle which fits in the highlighted triangle: an isosceles triangle where the base is twice the height. Let the base be 2 and the height be 1.
If the height of the rectangle is \(h\), then its width is \(2(1-h)\). Therefore its area is \(2h-2h^2\). By differentiation, it can be seen that this is maximum when \(h=\frac{1}{2}\), which means that ratio of the rectangle's length to its width is 2:1.
Extension
If the corner was not a 90° angle, then what is the largest area rectangle which could fit round it?
![](javascript:showlimage("piano.png"))
![](javascript:showlimage("piano-ans.png"))
![](javascript:showlimage("piano-ans2.png"))