Puzzles
Cross diagonal cover problem
Draw with an \(m\times n\) rectangle, split into unit squares. Starting in the top left corner, move at 45° across
the rectangle. When you reach the side, bounce off. Continue until you reach another corner of the rectangle:
How many squares will be coloured in when the process ends?
Show answer
Hide answer
$$\mathrm{lcm}(m-1,n-1)+1 - \frac12\left(\frac{\mathrm{lcm}(m-1,n-1)}{m-1}-1\right)\left(\frac{\mathrm{lcm}(m-1,n-1)}{n-1}-1\right)$$
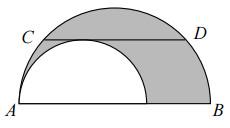
Two semicircles
The diagram shows two semicircles.
\(CD\) is a chord of the larger circle and is parallel to \(AB\). The length of \(CD\) is 8m. What is the area of the shaded region (in terms of \(\pi\))?
Show answer & extension
Hide answer & extension
The question does not fix the length of \(AB\), yet implies that there is a unique answer. Therefore we can take \(AB\) to be any length we like and expect the right answer. If \(AB\) is 8m long, then the unshaded semicircle has no area. Therefore the shaded area is \(\tfrac12\pi\times4^2=8\pi\)m.
Extension
How would you calculate the area if you don't assume that the length of \(AB\) doesn't affect the area?
21 December
To get today's number, multiply the number of modules needed to make a dodecahedron by half the number of tube maps used to make a stellated rhombicuboctahedron.
Show answer
Hide answer
One module is needed for each edge of the dodecahedron. Therefore 30 modules are needed.
48 tube maps are needed for the stellated rhombicuboctahedron.
Therefore today's number is 720.
1 December
What is area of the largest area rectangle which will fit in a circle of radius 10?
Show answer
Hide answer
The largest rectangle will be a square. 20 (double the radius) will be the length of its diagonal.
By Pythagoras' Theorem, the sides of the square are \(10\sqrt{2}\). Therefore the area of the square is 200.
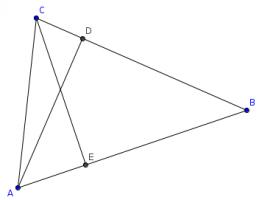
Cutting corners
The diagram below shows a triangle \(ABC\). The line \(CE\) is perpendicular to \(AB\) and the line \(AD\) is perpedicular to \(BC\).
The side \(AC\) is 6.5cm long and the lines \(CE\) and \(AD\) are 5.6cm and 6.0cm respectively.
How long are the other two sides of the triangle?
Show answer
Hide answer
Let \(A\), \(B\) and \(C\) represent the angles at points \(A\), \(B\) and \(C\). Looking at triangle \(ACE\) gives:
$$\sin A=\frac{5.6}{6.5}$$
And triangle \(ACD\) gives:
$$\sin C=\frac{6.0}{6.5}$$
Using Pythagoras' Theorem to find the missing sides in these triangles also gives:
$$\cos A=\frac{3.3}{6.5}$$
$$\cos C=\frac{2.5}{6.5}$$
We can use these to find \(\sin B\):
$$\begin{array}{rl}
\sin B&=\sin(\pi-A-C)\\
&=\sin(A+B)\\
&=\sin A\cos C + \cos A\sin C\\
&=\frac{5.6}{6.5}\frac{2.5}{6.5}+\frac{6.0}{6.5}\frac{3.3}{6.5}\\
&=\frac{33.8}{6.5^2}
\end{array}$$
Now the missing sides can be found using the sine rule:
$$\begin{array}{rl}
CB&=\frac{CA\sin A}{\sin B}\\
&=\frac{6.5\times\frac{5.6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times5.6}{33.8}\\
&=7\text{cm}
\end{array}$$
$$\begin{array}{rl}
AB&=\frac{CA\sin C}{\sin B}\\
&=\frac{6.5\times\frac{6}{6.5}}{\frac{33.8}{6.5^2}}\\
&=\frac{6.5^2\times6}{33.8}\\
&=7.5\text{cm}
\end{array}$$
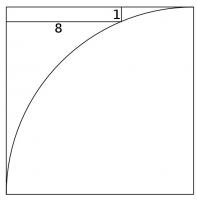
Quarter circle
Source: Maths Jam
A quarter circle is drawn in a square. A rectangle is drawn in the corner of the square which touches the circle and has sides of length 8 and 1.
What is the length of a side of the square?
Show answer
Hide answer
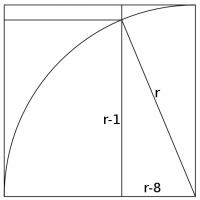
Let the radius of the circle by \(r\). Draw in the following two lines.
The sides of the triangle formed are \(r\), \(r-1\) and \(r-8\). By Pythagoras' Theorem:
$$(r-1)^2+(r-8)^2=r^2$$
$$r^2-2r+1+r^2-16r+64=r^2$$
$$r^2-18r+65=0$$
$$(r-13)(r-5)=0$$
$$r=5\text{ or }13$$
\(r\) must be larger than 8, \(r=13\).
Balanced sets
A set of points in the plane is called 'balanced' if for any two points \(A\) and \(B\) in the set, there is another point \(C\) in the set such that \(AC=BC\) (here \(AC\) is the distance between \(A\) and \(C\)).
For all \(n\geq3\), find a balanced set of \(n\) points.
Show answer
Hide answer
If \(n\) is odd, the vertices of a regular \(n\)-gon are balanced.
If \(n\) is even, a balanced set can be constructed as follows:
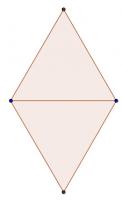
If \(n=4\), this set is balanced (both the triangles are equilateral):
Draw a triangle with its centre at one of the points, going through the other three points:
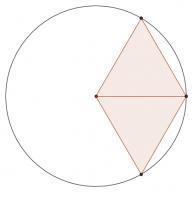
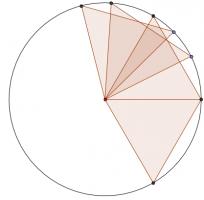
For \(n>4\), repeatedly add a two new points on the circle which form an equilateral triangle with the centre. For example, for \(n=6\), this set is balanced:
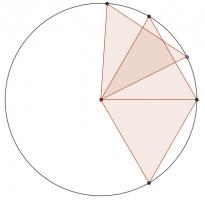
And for \(n=8\), this set is balanced:
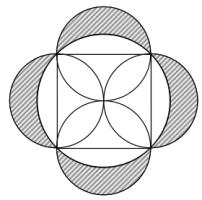
Squared circle
Each side of a square has a circle drawn on it as diameter. The square is also inscribed in a fifth circle as shown.
Find the ratio of the total area of the shaded crescents to the area
of the square.
Show answer
Hide answer
Let the radius of the small circles be \(r\). The are of half of one of these circles is \(\frac{1}{2}\pi r^2\).
The side of the square is \(2r\) and so the area of the square is \(4r^2\). Therefore the area of the whole shape is \((4+2\pi)r^2\).
By Pythagoras' Theorem, the radius of the large circle is \(r\sqrt{2}\). Therefore the area of the circle is \(2\pi r^2\). This means that the shaded area is \((4+2\pi)r^2 - 2\pi r^2\) or \(4r^2\).
This is the same as the area of the square, so the ratio is 1:1.
![](javascript:showlimage("cross_p1.png"))
![](javascript:showlimage("cross_p2.png"))
![](javascript:showlimage("cross_p3.png"))
![](javascript:showlimage("cross_p4.png"))
![](javascript:showlimage("cross_p5.png"))
![](javascript:showlimage("cross_pend.png"))
![](javascript:showlimage("two-semicircles.jpg"))
![](javascript:showlimage("cut-corn.png"))
![](javascript:showlimage("quarter-circle.jpg"))
![](javascript:showlimage("quarter-circle-ans.jpg"))
![](javascript:showlimage("balanced-a1.png"))
![](javascript:showlimage("balanced-a1andahalf.png"))
![](javascript:showlimage("balanced-a2.png"))
![](javascript:showlimage("balanced-a3.png"))
![](javascript:showlimage("circles-and-squares.png"))