Puzzles
Balanced sets
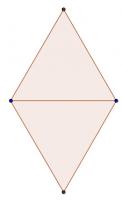
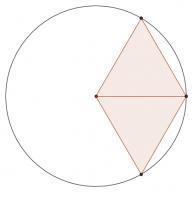
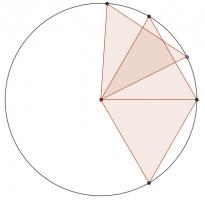
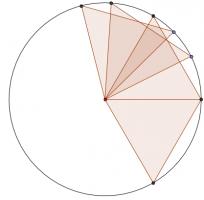
A set of points in the plane is called 'balanced' if for any two points \(A\) and \(B\) in the set, there is another point \(C\) in the set such that \(AC=BC\) (here \(AC\) is the distance between \(A\) and \(C\)).
For all \(n\geq3\), find a balanced set of \(n\) points.
![](javascript:showlimage("balanced-a1.png"))
![](javascript:showlimage("balanced-a1andahalf.png"))
![](javascript:showlimage("balanced-a2.png"))
![](javascript:showlimage("balanced-a3.png"))
If you enjoyed this puzzle, check out Sunday Afternoon Maths XLIV,
puzzles about coordinates, or a random puzzle.
puzzles about coordinates, or a random puzzle.