Puzzles
Find them all
Find all continuous positive functions, \(f\) on \([0,1]\) such that:
$$\int_0^1 f(x) dx=1\\
\mathrm{and }\int_0^1 xf(x) dx=\alpha\\
\mathrm{and }\int_0^1 x^2f(x) dx=\alpha^2$$
Show answer & extension
Hide answer & extension
$$0=\alpha^2-2\alpha^2+\alpha^2\\
=\int_0^1 x^2f(x) dx-2\int_0^1 \alpha xf(x) dx+\int_0^1 \alpha^2f(x)dx\\
=\int_0^1 (x^2-2\alpha x+\alpha^2)f(x)dx\\
=\int_0^1 (x-\alpha)^2 f(x)dx$$
\(f(x)\) and \((x-\alpha)^2\) are both positive so this is only possible if one of them if always zero.
But \((x-\alpha)^2\) is only zero when \(x=\alpha\) and \(\int_0^1 f(x) dx=1\) so \(f(x)\) cannot always be zero. Therefore no such function exists.
Extension
Find all continuous positive functions, \(f\) on \([0,1]\) such that:
$$\int_0^1 f(x) dx=1\\
\int_0^1 xf(x) dx=1\\$$
Four points on a shape
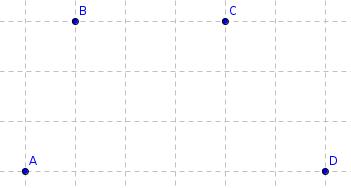
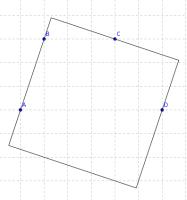
Fiona wants to draw a 2-dimensional shape whose perimeter passes through the points A, B, C and D
Which of the following shapes can she draw?
(i) A circle
(ii) An equilateral triangle
(iii) A square
Show answer & extension
Hide answer & extension
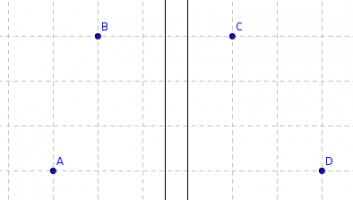
(i) If a circle could be drawn, then its centre would be equidistant from each pair of points. But the locus of points equidistant from B and C is parallel to the locus of points equidistant from A and D.
Therefore it is impossible to place the centre of the circle, so no circle can be drawn.
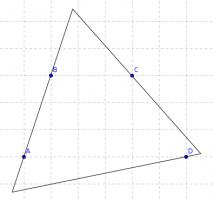
(ii)
(iii)
Extension
Let A, B, C and D be any four points. When is it possible to draw
(i) A circle
(ii) An equilateral triangle
(iii) A square
through the four points?
Algebraic fractions
Given that
$$\frac{3x+y}{x-3y}=-1$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
Show answer & extension
Hide answer & extension
$$\frac{3x+y}{x-3y}=-1$$
implies that
$$3x+y=3y-x\\
2x=y$$
This means that
$$\frac{x+3y}{3x-y}=\frac{x+6x}{3x-2x}\\
=\frac{7x}{x}\\=7$$
Extension
Given that
$$\frac{3x+y}{x-3y}=-k$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
For which values of \(k\) is the answer an integer?
Four integers
\(a\), \(b\), \(c\) and \(d\) are four positive (and non-zero) integers.
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=2009$$
What is the value of \(a+b+c+d\)?
Show answer & extension
Hide answer & extension
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=(a+1)(b+1)(c+1)(d+1)-1$$
So:
$$(a+1)(b+1)(c+1)(d+1)=2010\\=2\times 3\times 5\times 67$$
Therefore \(a+b+c+d=1+2+4+66=73\).
Extension
Which numbers could 2009 be replaced with so that the problem still has a unique solution?
Sum
What is
$$\sum_{i=1}^{\infty}\frac{1}{i 2^i}$$
?
Show answer & extension
Hide answer & extension
Write \(x\) instead of 2. Now we find that:
$$\frac{d}{dx}\sum_{i=1}^{\infty}\frac{1}{i x^i}=\sum_{i=1}^{\infty}\frac{-1}{x^{i+1}}\\
=-\frac{1}{x}\sum_{i=1}^{\infty}\frac{1}{x^i}\\
=-\frac{1}{x}\times\frac{1}{x-1}\\
=\frac{1}{x}+\frac{1}{1-x}$$
The sum we are after is the integral of this:
$$\sum_{i=1}^{\infty}\frac{1}{i x^i}=\ln|x|+\ln|1-x|$$
When \(x=2\), this is \(\ln(2)\)
Extension
What is
$$\sum_{i=1}^{\infty}\frac{1}{i^2 2^i}$$
?
Fair dice
Timothy and Urban are playing a game with two six-sided dice. The dice are unusual: Rather than bearing a number, each face is painted either red or blue.
The two take turns throwing the dice. Timothy wins if the two top faces are the same color, and Urban wins if they're different. Their chances of winning are equal.
The first die has 5 red faces and 1 blue face. What are the colours on the second die?
Show answer & extension
Hide answer & extension
Let \(A\) and \(B\) be the outcomes of the two dice. Let \(p\) be the probability that the second die lands on red. The probability of the dice being the same is:
$$\frac{1}{2}=\mathbb{P}(A=r)\mathbb{P}(B=r)+\mathbb{P}(A=b)\mathbb{P}(B=b)\\
=\frac{5}{6}p+\frac{1}{6}(1-p)\\
=\frac{1}{6}+\frac{4}{6}p
$$
This means that:
$$\frac{4}{6}p=\frac{1}{2}-\frac{1}{6}\\
=\frac{1}{3}\\
p=\frac{\frac{1}{3}}{\frac{4}{6}}=\frac{1}{2}$$
Extension
If the first die has \(n\) red faces and \(6-n\) blue faces, what colours are on the second die?
Half digits
Can you use each of the digits 1 to 9 to make a fraction which is equal to a half?
Pizza
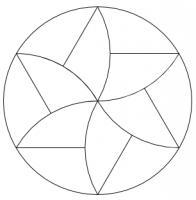
Twelve friends want to share a pizza. One of the friends is very fussy and will not eat the centre of the pizza.
Is it possible to split a (circular) pizza into twelve identical pieces such that there is at least one piece which does not touch the centre?