Puzzles
Frogs
Two frogs and two toads are standing on five lily pads.
The frogs and toads need to pass each other. They can only move by jumping one or two lily pads forward. In jumping two pads forwards they can jump over other frogs or toads.
How many jumps need to be made to get the frogs and toads past each other?
Show answer & extension
Hide answer & extension
Representing the frogs as \(F\), the toads as \(T\) and the spaces as \(\), the solution is as follows:
$$
F\ F\ \_\ T\ T\\
F\ \_\ F\ T\ T\\
F\ T\ F\ \_\ T\\
F\ T\ F\ T\ \_\\
F\ T\ \_\ T\ F\\
\_\ T\ F\ T\ F\\
T\ \_\ F\ T\ F\\
T\ T\ F\ \_\ F\\
T\ T\ \_\ F\ F\\
$$
Eight moves are required.
Extension
If there are three frogs on each side, how many moves are needed?
If there are three frogs on one side and two on the other, how many moves are needed?
If there are \(n\) frogs on one side and \(m\) on the other, how many moves are needed?
The blue-eyed sisters
If you happen to meet two of the Jones sister (two sisters chosen at random from all the Jones sisters), it is exactly an even-money bet that both will be blue-eyed. What is your best guess of the total number of Jones sisters?
Show answer & extension
Hide answer & extension
If there are \(n\) sisters and \(k\) of these sisters have blue eyes, then the probability of the two sisters having blue eyes is:
$$\frac{\left(\begin{array}{c}k\\2\end{array}\right)}{\left(\begin{array}{c}n\\2\end{array}\right)}
\\
=\frac{k(k-1)}{n(n-1)}=\frac{1}{2}
$$
This means that:
$$2k(k-1)=n(n-1)$$
The smallest integer solution of this is when there are 4 sisters, 3 of whom have blue eyes.
The next smallest integer solution is when there are 21 sisters, 15 of whom have blue eyes. There are unlikely to be as many as 21 sisters, so 4 sisters are the most likely.
Extension
What is the next integer solution after 21 sisters?
1089
Take a three digit number. Reverse the digits then take the smaller number from the larger number.
Next add the answer to its reverse.
For example, if 175 is chosen:
$$571-175=396$$
$$396+693=1089$$
What numbers is it possible to obtain as an answer, and when will each be obtained?
Show answer & extension
Hide answer & extension
Call the digits of the starting number \(A\), \(B\) and \(C\).
If the number is a palindrome (if \(A=C\)) then the answer to the subtraction will be 0, so the answer is 0.
If the first and last digits differ one, we can consider the case \(A=C+1\). The same analysis will apply to \(C=A+1\).
$$100C+10B+A-(100A+10B+C)=99C-99A$$
$$=99A+99-99A$$
$$=99$$
Then, \(99+99=198\) so the answer is 198
If the first and last digits differ by at least two, we can consider the case \(A=C+n\), where \(2\leq n\leq 9\). The same analysis will apply to \(C=A+n\).
$$100C+10B+A-(100A+10B+C)=99C-99A$$
$$=99(A+n)-99A$$
$$=99n$$
This number will be 198, 297, 396, 495, 594, 693, 792, 891 or 990. In each of these numbers, the middle digit is 9 and the two other digits add up to 9, so they can be written \(100n+90+(9-n)\). If we add this to its reverse:
$$100n+90+(9-n)+100(9-n)+90+n$$
$$=100n+99-n+900-100n+90+n$$
$$=900+99+90+100n-100n+n-n$$
$$=1089$$
So the three possible answers are 0, 99 and 1089 which will occur when the first and list digits of the number differ by 0, 1 or more respectively.
Extension
Which answers are possible if the numbers are written in different bases?
Which answers are possible if four digit numbers are taken? Or five digit numbers?
Integrals
$$\int_0^1 1 dx = 1$$
Find \(a_1\) such that:
$$\int_0^{a_1} x dx = 1$$
Find \(a_2\) such that:
$$\int_0^{a_2} x^2 dx = 1$$
Find \(a_n\) such that (for \(n>0\)):
$$\int_0^{a_n} x^n dx = 1$$
Show answer & extension
Hide answer & extension
$$1=\int_0^{a_1} x dx=\frac{a_1^2}{2}$$
So, \(a_1=\sqrt{2}\).
$$1=\int_0^{a_2} x^2 dx=\frac{a_2^3}{3}$$
So, \(a_2=3^{\frac{1}{3}}\).
$$1=\int_0^{a_n} x^n dx=\frac{a_n^{n+1}}{n+1}$$
So, \(a_n={(n+1)}^{\frac{1}{n+1}}\).
Extension
Find \(b_n\) such that (for \(n>1\)):
$$\int_{b_n}^{\infty} x^{-n} dx = 1$$
Tetrahedral die
When a tetrahedral die is rolled, it will land with a point at the top: there is no upwards face on which the value of the roll can be printed. This is usually solved by printing three numbers on each face and the number which is at the bottom of the face is the value of the roll.
Is it possible to make a tetrahedral die with one number on each face such that the value of the roll can be calculated by adding up the three visible numbers? (the values of the four rolls must be 1, 2, 3 and 4)
Show answer & extension
Hide answer & extension
Let \(a\), \(b\), \(c\) and \(d\) be the numbers on the four faces. The following simultaneous equations must hold:
$$a+b+c=1$$
$$a+b+d=2$$
$$a+c+d=3$$
$$b+c+d=4$$
These can be solved to find that the numbers on the faces must be \(-\frac{2}{3}\), \(\frac{1}{3}\), \(\frac{4}{3}\) and \(\frac{7}{3}\).
Extension
Is it possible to make a six-sided die with one number on each face such that the value of the roll can be calculated by adding up the five visible numbers?
Is it possible to make an \(n\)-sided die with one number on each face such that the value of the roll can be calculated by adding up the \((n-1)\) visible numbers?
Is it possible to make a die with one integer on each face such that the value of the roll can be calculated by adding up the visible numbers?
No change
"Give me change for a dollar, please," said the customer.
"I'm sorry," said the cashier, "but I can't do it with the coins I have. In fact, I can't change a half dollar, quarter, dime or nickel."
"Do you have any coins at all?" asked the customer.
"Oh yes," said the cashier, "I have $1.15 in coins."
Which coins are in the cash register?
(The available coins are 50¢, 25¢, 10¢ 5¢ and 1¢.)
Dirty work
Timothy, Urban, and Vincent are digging identical holes in a field.
When Timothy and Urban work together, they dig 1 hole in 4 days.
When Timothy and Vincent work together, they dig 1 hole in 3 days.
When Urban and Vincent work together, they dig 1 hole in 2 days.
Working alone, how long does it take Timothy to dig one hole?
Show answer & extension
Hide answer & extension
Let \(t\), \(u\) and \(v\) be the prortion of a hole dug in one day by Timothy, Urban and Vincent respectively. Then the following equations hold:
$$4t+4u=1$$$$3t+3v=1$$$$2u+2v=1$$
These can be solved to find that \(t=\frac{1}{24}\) so it will take Timothy 24 days to dig a hole.
Extension
Working alone, how long does it take Urban to dig one hole?
Working alone, how long does it take Vincent to dig one hole?
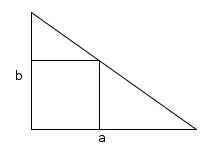
Square in a triangle
A right-angled triangle has short sides of length \(a\) and \(b\). A square is drawn in the triangle so that two sides lie on the sides of the triangle and a corner lies on the hypotenuse.
What is the length of a side of the square?
Show answer & extension
Hide answer & extension
Call the length of a side of the square \(x\). CAB and CEF are similar triangles, therefore:
$$\frac{EF}{AB}=\frac{EC}{AC}$$
$$\frac{x}{a}=\frac{b-x}{b}$$
$$bx=ab-ax$$
$$x=\frac{ab}{a+b}$$
Extension
Consider a tetrahedron with vertices at \((0,0,0)\), \((a,0,0)\), \((0,b,0)\) and \((0,0,c)\). A cube is placed in the tetrahedron so that three of its faces are in the xy, xz and yz planes and one of its vertices lies on the other face.
What is the length of a side of the cube?