Puzzles
Half an equilateral triangle
What is the shortest straight line which bisects an equilateral triangle?
Show answer & extension
Hide answer & extension
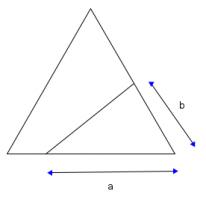
Consider a line which bisects an equilateral triangle with sides of length 1. Let the sides of the smaller triangle created be \(a\) and \(b\) as shown below:
The area of the equilateral triangle is:
$$\frac{1}{2}\times 1\times 1\times \sin(60)\\=\frac{\sqrt{3}}{4}$$
The area of the smaller triangle is:
$$\frac{1}{2}ab \sin(60)\\=\frac{ab\sqrt{3}}{4}$$
This is half the area of the equilateral triangle, so:
$$ab=\frac{1}{2}$$
The length (\(L\)) of the line bisecting the equilateral triangle is:
$$L=a^2+b^2-2ab\cos(60)\\
=a^2+\left(\frac{1}{2a}\right)^2-\frac{2a}{2a}\times \frac{1}{2}\\
=a^2+\frac{1}{4a^2}-\frac{1}{2}$$
To find the minimum, we set the derivative to 0:
$$0=\frac{dL}{da}=2a-\frac{1}{2a^3}\\
4a^4-1=0\\
a^4=\frac{1}{4}\\
a=\frac{1}{\sqrt{2}}$$
For this value of \(a\), \(b\) and \(L\) also equal to \(\frac{1}{\sqrt{2}}\).
Extension
What if the line does not need to be straight?
Marbles
A bag contains \(m\) blue and \(n\) yellow marbles. One marble is selected at random from the bag and its colour is noted. It is then returned to the bag along with \(k\) other marbles of the same colour. A second marble is now selected at random from the bag. What is the probability that the second marble is blue?
Show answer & extension
Hide answer & extension
Let \(M_1\) be colour of the first marble and \(M_2\) be the colour of the second marble
$$\mathbb{P}(M_2=\mathrm{blue})=\mathbb{P}(M_2=\mathrm{blue}|M_1=\mathrm{blue})\mathbb{P}(M_1=\mathrm{blue})\\+\mathbb{P}(M_2=\mathrm{blue}|M_1=\mathrm{yellow})\mathbb{P}(M_1=\mathrm{yellow})\\
=\left(\frac{m+k}{m+n+k}\right)\left(\frac{m}{m+n}\right)+\left(\frac{m}{m+n+k}\right)\left(\frac{n}{m+n}\right)\\
=\frac{m(m+k)+mn}{(m+n)(m+n+k)}\\
=\frac{m(m+n+k)}{(m+n)(m+n+k)}\\
=\frac{m}{m+n}
$$
Extension
A bag contains \(m\) blue and \(n\) yellow marbles. One marble is selected at random from the bag and its colour is noted. It is then returned to the bag along with \(k\) other marbles of the same colour and \(l\) marbles of the other colour. A second marble is now selected at random from the bag. What is the probability that the second marble is blue?
37
Take a three digit number where all the digits are the same (eg. 888).
Divide this number by the sum of its digits (eg. 888÷24).
Your answer is 37.
Prove that the answer will always be 37.
Show answer & extension
Hide answer & extension
Let the chosen digit be \(n\). The three digit number will be \(100n+10n+1n\) or \(111n\). The sum of the digits will be \(n+n+n\) or \(3n\). Therefore the division is:
$$\frac{111n}{3n}=\frac{111}{3}\\=37$$
Extension
If the numbers are written is a base other than 10, will this trick work? How could it be adapted to work in any base?
Find them all
Find all continuous positive functions, \(f\) on \([0,1]\) such that:
$$\int_0^1 f(x) dx=1\\
\mathrm{and }\int_0^1 xf(x) dx=\alpha\\
\mathrm{and }\int_0^1 x^2f(x) dx=\alpha^2$$
Show answer & extension
Hide answer & extension
$$0=\alpha^2-2\alpha^2+\alpha^2\\
=\int_0^1 x^2f(x) dx-2\int_0^1 \alpha xf(x) dx+\int_0^1 \alpha^2f(x)dx\\
=\int_0^1 (x^2-2\alpha x+\alpha^2)f(x)dx\\
=\int_0^1 (x-\alpha)^2 f(x)dx$$
\(f(x)\) and \((x-\alpha)^2\) are both positive so this is only possible if one of them if always zero.
But \((x-\alpha)^2\) is only zero when \(x=\alpha\) and \(\int_0^1 f(x) dx=1\) so \(f(x)\) cannot always be zero. Therefore no such function exists.
Extension
Find all continuous positive functions, \(f\) on \([0,1]\) such that:
$$\int_0^1 f(x) dx=1\\
\int_0^1 xf(x) dx=1\\$$
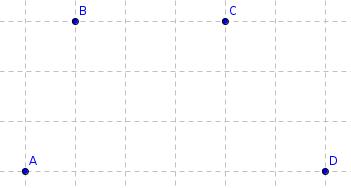
Four points on a shape
Fiona wants to draw a 2-dimensional shape whose perimeter passes through the points A, B, C and D
Which of the following shapes can she draw?
(i) A circle
(ii) An equilateral triangle
(iii) A square
Show answer & extension
Hide answer & extension
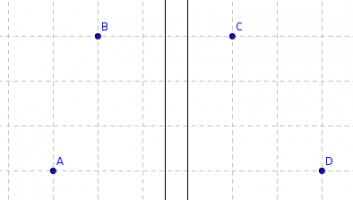
(i) If a circle could be drawn, then its centre would be equidistant from each pair of points. But the locus of points equidistant from B and C is parallel to the locus of points equidistant from A and D.
Therefore it is impossible to place the centre of the circle, so no circle can be drawn.
(ii)
(iii)
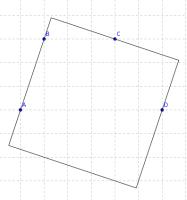
Extension
Let A, B, C and D be any four points. When is it possible to draw
(i) A circle
(ii) An equilateral triangle
(iii) A square
through the four points?
Algebraic fractions
Given that
$$\frac{3x+y}{x-3y}=-1$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
Show answer & extension
Hide answer & extension
$$\frac{3x+y}{x-3y}=-1$$
implies that
$$3x+y=3y-x\\
2x=y$$
This means that
$$\frac{x+3y}{3x-y}=\frac{x+6x}{3x-2x}\\
=\frac{7x}{x}\\=7$$
Extension
Given that
$$\frac{3x+y}{x-3y}=-k$$
what is the value of
$$\frac{x+3y}{3x-y}$$
?
For which values of \(k\) is the answer an integer?
Four integers
\(a\), \(b\), \(c\) and \(d\) are four positive (and non-zero) integers.
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=2009$$
What is the value of \(a+b+c+d\)?
Show answer & extension
Hide answer & extension
$$abcd+abc+bcd+cda+dab+ab+bc+cd+da+ac+bd\\+a+b+c+d=(a+1)(b+1)(c+1)(d+1)-1$$
So:
$$(a+1)(b+1)(c+1)(d+1)=2010\\=2\times 3\times 5\times 67$$
Therefore \(a+b+c+d=1+2+4+66=73\).
Extension
Which numbers could 2009 be replaced with so that the problem still has a unique solution?
Sum
What is
$$\sum_{i=1}^{\infty}\frac{1}{i 2^i}$$
?
Show answer & extension
Hide answer & extension
Write \(x\) instead of 2. Now we find that:
$$\frac{d}{dx}\sum_{i=1}^{\infty}\frac{1}{i x^i}=\sum_{i=1}^{\infty}\frac{-1}{x^{i+1}}\\
=-\frac{1}{x}\sum_{i=1}^{\infty}\frac{1}{x^i}\\
=-\frac{1}{x}\times\frac{1}{x-1}\\
=\frac{1}{x}+\frac{1}{1-x}$$
The sum we are after is the integral of this:
$$\sum_{i=1}^{\infty}\frac{1}{i x^i}=\ln|x|+\ln|1-x|$$
When \(x=2\), this is \(\ln(2)\)
Extension
What is
$$\sum_{i=1}^{\infty}\frac{1}{i^2 2^i}$$
?
![](javascript:showlimage("bisecting-equilateral.png"))
![](javascript:showlimage("four-points.png"))
![](javascript:showlimage("four-points-circle.png"))
![](javascript:showlimage("four-points-triangle.png"))
![](javascript:showlimage("four-points-square.png"))