Hide answer & extension
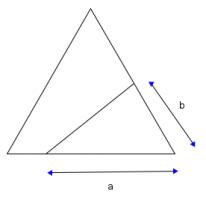
Consider a line which bisects an equilateral triangle with sides of length 1. Let the sides of the smaller triangle created be \(a\) and \(b\) as shown below:
The area of the equilateral triangle is:
$$\frac{1}{2}\times 1\times 1\times \sin(60)\\=\frac{\sqrt{3}}{4}$$
The area of the smaller triangle is:
$$\frac{1}{2}ab \sin(60)\\=\frac{ab\sqrt{3}}{4}$$
This is half the area of the equilateral triangle, so:
$$ab=\frac{1}{2}$$
The length (\(L\)) of the line bisecting the equilateral triangle is:
$$L=a^2+b^2-2ab\cos(60)\\
=a^2+\left(\frac{1}{2a}\right)^2-\frac{2a}{2a}\times \frac{1}{2}\\
=a^2+\frac{1}{4a^2}-\frac{1}{2}$$
To find the minimum, we set the derivative to 0:
$$0=\frac{dL}{da}=2a-\frac{1}{2a^3}\\
4a^4-1=0\\
a^4=\frac{1}{4}\\
a=\frac{1}{\sqrt{2}}$$
For this value of \(a\), \(b\) and \(L\) also equal to \(\frac{1}{\sqrt{2}}\).
Extension
What if the line does not need to be straight?
![](javascript:showlimage("bisecting-equilateral.png"))