Puzzles
Equal side and angle
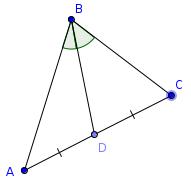
In the diagram shown, the lengths \(AD = CD\) and the angles \(ABD=CBD\).
Prove that the lengths \(AB=BC\).
Show answer
Hide answer
By the sine rule in BCD:
$$\frac{CD}{\sin(CBD)}=\frac{BD}{\sin(BCD)}$$
By the sine rule in BAD:
$$\frac{AD}{\sin(ABD)}=\frac{BD}{\sin(BAD)}$$
\(ABD=CBD\) and \(AD=CD\), so:
$$\sin(BAD)=\frac{BD\sin(ABD)}{AD}\\
=\frac{BD\sin(CBD)}{CD}\\
=\sin(BCD)$$
Using the sine rule in ABC:
$$\frac{AB}{\sin(BCD)}=\frac{BC}{\sin(BAD)}$$
The two sines are equal and so:
$$AB=BC$$
Arctan
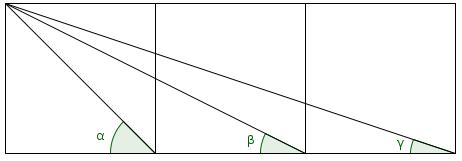
Prove that \(\arctan(1)+\arctan(2)+\arctan(3)=\pi\).
Show answer & extension
Hide answer & extension
Let \(\alpha=\arctan(1)\), \(\beta=\arctan(2)\) and \(\gamma=\arctan(3)\), then draw the angles as follows:
Extension
Can you find any other integers \(a\), \(b\) and \(c\) such that:
$$\arctan(a)+\arctan(b)+\arctan(c)=\pi$$
A bit of Spanish
Each of the letters P, O, C, M, U and H represent a different digit from 0 to 9.
Which digit does each letter represent?
Show answer & extension
Hide answer & extension
POCO is 4595 and MUCHO is 68925.
Extension
The question could be written as \(POCO\times 15=MUCHO\).
For which values of \(n\) are the letters uniquely defined by \(POCO\times n = MUCHO\)?
Square deal
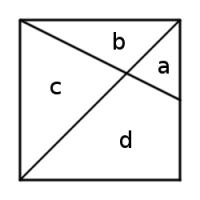
This unit square is divided into four regions by a diagonal and a line that connects a vertex to the midpoint of an opposite side. What are the areas of the four regions?
Show answer & extension
Hide answer & extension
The square is unit, so \(a+b+c+d=1\). By the definitions of the lines, \(a+d=\frac{1}{2}\) and \(a+b=\frac{1}{4}\).
\(a\) and \(c\) are similar triangles. The vertical side of \(c\) is twice that of \(a\) so \(c=4a\).
Therefore we have the system of simultaneous equations:
$$a+b+c+d=1\\a+d=\frac{1}{2}\\a+b=\frac{1}{4}\\c=4a$$
These can be solved to find:
$$a=\frac{1}{12}\\b=\frac{1}{6}\\c=\frac{1}{3}\\d=\frac{5}{12}\\$$
Extension
What would be the areas if the lines were a diagonal and another line which divides the sides in the ratio \(x:y\)?
Odd squares
Prove that 1 and 9 are the only square numbers where all the digits are odd.
Show answer & extension
Hide answer & extension
If \(n^2\) has all odd digits then the units digit of \(n\) must be odd. It can be checked that \(n\) cannot be a one digit number (except 1 or 3 as given in the question) as the tens digit will be even.
Therefore \(n\) can be written as \(10A+B\) where \(A\) is a positive integer and \(B\) is an odd positive integer.
$$n^2=(10A+B)^2\\=100A+20AB+B^2$$
Now consider the tens digit of this.
\(100A\) has no effect on this digit. The tens digit of \(20AB\) will be the units digit of \(2AB\) which will be even. The tens digit of \(B^2\) is even (as checked above). Therefore the tens digit of \(n^2\) is even.
Hence 1 and 9 are the only square numbers where all the digits are odd.
Extension
For which bases is this not true?
Half an equilateral triangle
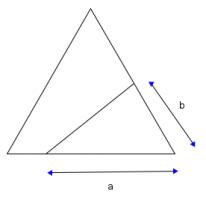
What is the shortest straight line which bisects an equilateral triangle?
Show answer & extension
Hide answer & extension
Consider a line which bisects an equilateral triangle with sides of length 1. Let the sides of the smaller triangle created be \(a\) and \(b\) as shown below:
The area of the equilateral triangle is:
$$\frac{1}{2}\times 1\times 1\times \sin(60)\\=\frac{\sqrt{3}}{4}$$
The area of the smaller triangle is:
$$\frac{1}{2}ab \sin(60)\\=\frac{ab\sqrt{3}}{4}$$
This is half the area of the equilateral triangle, so:
$$ab=\frac{1}{2}$$
The length (\(L\)) of the line bisecting the equilateral triangle is:
$$L=a^2+b^2-2ab\cos(60)\\
=a^2+\left(\frac{1}{2a}\right)^2-\frac{2a}{2a}\times \frac{1}{2}\\
=a^2+\frac{1}{4a^2}-\frac{1}{2}$$
To find the minimum, we set the derivative to 0:
$$0=\frac{dL}{da}=2a-\frac{1}{2a^3}\\
4a^4-1=0\\
a^4=\frac{1}{4}\\
a=\frac{1}{\sqrt{2}}$$
For this value of \(a\), \(b\) and \(L\) also equal to \(\frac{1}{\sqrt{2}}\).
Extension
What if the line does not need to be straight?
Marbles
A bag contains \(m\) blue and \(n\) yellow marbles. One marble is selected at random from the bag and its colour is noted. It is then returned to the bag along with \(k\) other marbles of the same colour. A second marble is now selected at random from the bag. What is the probability that the second marble is blue?
Show answer & extension
Hide answer & extension
Let \(M_1\) be colour of the first marble and \(M_2\) be the colour of the second marble
$$\mathbb{P}(M_2=\mathrm{blue})=\mathbb{P}(M_2=\mathrm{blue}|M_1=\mathrm{blue})\mathbb{P}(M_1=\mathrm{blue})\\+\mathbb{P}(M_2=\mathrm{blue}|M_1=\mathrm{yellow})\mathbb{P}(M_1=\mathrm{yellow})\\
=\left(\frac{m+k}{m+n+k}\right)\left(\frac{m}{m+n}\right)+\left(\frac{m}{m+n+k}\right)\left(\frac{n}{m+n}\right)\\
=\frac{m(m+k)+mn}{(m+n)(m+n+k)}\\
=\frac{m(m+n+k)}{(m+n)(m+n+k)}\\
=\frac{m}{m+n}
$$
Extension
A bag contains \(m\) blue and \(n\) yellow marbles. One marble is selected at random from the bag and its colour is noted. It is then returned to the bag along with \(k\) other marbles of the same colour and \(l\) marbles of the other colour. A second marble is now selected at random from the bag. What is the probability that the second marble is blue?
37
Take a three digit number where all the digits are the same (eg. 888).
Divide this number by the sum of its digits (eg. 888÷24).
Your answer is 37.
Prove that the answer will always be 37.
Show answer & extension
Hide answer & extension
Let the chosen digit be \(n\). The three digit number will be \(100n+10n+1n\) or \(111n\). The sum of the digits will be \(n+n+n\) or \(3n\). Therefore the division is:
$$\frac{111n}{3n}=\frac{111}{3}\\=37$$
Extension
If the numbers are written is a base other than 10, will this trick work? How could it be adapted to work in any base?